Минимальное расстояние от плиты до вытяжки: Расстояние от плиты до вытяжки
Расстояние от плиты до вытяжки: стандарты и нормы установки
Кухня – сложное пространство, которое подвергается ежедневно многочисленным нагрузкам. И для того чтобы воздух в помещении всегда был свежим, необходимо тщательно продумывать вентиляцию и обязательно устанавливать вытяжку. Она буде работать эффективно в одном случае: если правильно рассчитать расстояние от плиты до вытяжки. Неправильный монтаж не затруднит приготовление пищи, но сделает работу прибора совершенно бесполезной. Поэтому так важно знать, какие типы вытяжек существуют, какие условия монтажа важно соблюдать во время установки.
Конструктивные особенности вытяжных систем
Принцип действия описываемого прибора предельно прост: конструкция обеспечивает принудительный забор грязного воздуха и его очистку от продуктов сгорания газа, запаха, компонентов дыма, который формируется во время приготовления пищи. Что такое вытяжка? Это прибор, имеющий корпус, панель, обеспечивающую забор воздуха, определенный набор фильтров и элемент принудительной вентиляции.
Все системы по принципу работы можно поделить на две большие группы:
- Приборы по типу устройства на принудительном выводе воздуха за пределы кухни. Такая установка, расположенная над варочной панелью, обеспечивает полное удаление гари и копоти, но для создания комфортного микроклимата важно тщательно продумывать приток свежего воздуха. Перед тем, как решать вопрос о том, как повесить вытяжку, необходимо продумывать подобные технические моменты.
- Циркуляционный принцип работы не выводит грязный воздух из помещения, а при помощи системы фильтров очищает его и возвращает обратно в комнату. Данная очистка занимает много времени, но для ее функционирования не нужно устанавливать дополнительно вереницу дополнительных технических магистралей.
Обратите внимание! Обе системы представлены несколькими моделями. Правильная высота установки вытяжки над плитой рассчитывается с учетом конструктивных особенностей описываемых приборов.
Виды вытяжных систем
Подвесная установка имеет плоскую форму, она крепится снизу полки кухонного гарнитура непосредственно над электроплитой или газовой горелкой. Внутри конструкции обязательно есть вентиляторы, которые обеспечивают процесс всасывания загрязненного воздуха. Он проводится через фильтры и очищается, расстояние между плитой и вытяжкой при монтаже подвесной модели может варьироваться в пределах от 65-75 см для электроплит и 75-85 см для газовых варочных панелей.
Внутри конструкции обязательно есть вентиляторы, которые обеспечивают процесс всасывания загрязненного воздуха. Он проводится через фильтры и очищается, расстояние между плитой и вытяжкой при монтаже подвесной модели может варьироваться в пределах от 65-75 см для электроплит и 75-85 см для газовых варочных панелей.
Встраиваемый прибор является частью шкафа или купола, который устанавливают прямо над варочной поверхностью. Такая конструктивная особенность делает описываемый прибор совершенно незаметным. Выбирая такую модель, важно приобрести ту из них, ширина которой будет в точности совпадать с шириной плиты и с шириной кухонного шкафа. Расстояние между двумя предметами рассчитывается по стандартным параметрам (о них чуть ниже). Выбирая такой вариант исполнения важно еще при заказе кухни обговаривать с производителями мебели подобную конструктивную особенность.
Обратите внимание! Встраиваться описываемая установка может и непосредственно в столешницу, сразу же позади печи.
При такой комбинации ширина столешницы должна быть не менее 90 см.
Настенный вариант исполнения – самостоятельный элемент кухонного оборудования, который крепится к стене над варочной поверхностью. Выбирая его, важно знать о том, что расстояние замеряется от нижнего края панели вытяжки. Минимально допустимый показатель равен 35 см, максимальное расстояние от плиты до настенного воздухозаборника должно быть не более 45 см. В противном случае вытяжка просто не справиться с поставленными задачами.
Угловая модель предназначена для монтажа вытяжки в углу помещения.
Островные системы монтируются к потолку в центре большой просторной кухни. Они выбираются тогда, когда печь располагается посреди комнаты. Система крепится прямо над ней, вытяжка должна находиться на расстоянии в пределах существующего минимума или максимума. Главное, чтобы сама хозяйка при этом не касалась головой до корпуса вытяжной системы.
Выбор модели во многом зависит от того, какое расстояние между плиткой и вытяжкой по планировке расположения гарнитура существует.
Как рассчитать расстояние?
Решая вопрос о том, на какую высоту можно вешать вытяжку, необходимо на первое место ставить безопасность использования двух приборов. Как правило, корпуса вытяжек изготавливаются из пластика или из металла. Для того чтобы предотвратить возможность самовозгорания корпуса вытяжки, ее необходимо устанавливать на расстоянии 65-70 см от варочной поверхности.
Воздухоочиститель не должен мешать хозяйке, готовить пищу, пользуясь высокими большими кастрюлями.
Верхний предел расстояния вытяжки от газовой плиты или электрической модели должен обеспечивать возможность тянуть воздух из самых загрязненных слоев воздуха над варочной поверхностью.
Во многом высота вытяжки над газовой плитой и электрической варочной поверхностью зависит и от мощности самого прибора, площади его воздухозаборника. Понятно, что маломощный прибор (300 куб./ч) вешать высоко нет смысла. А вот мощные вытяжки на кухне (более 600 куб./ч) можно вешать, превышая средние рекомендуемые показатели.
Мощность вытяжки нужно рассчитывать, учитывая площадь кухни и высоту потолков. Расчеты производятся по определенной формуле: площадь помещения умножается на высоту потолков. Так, например, если кухня имеет площадь 6 кв.м., а высота потолка составляет 2,5 м, мощность вытяжки должна быть не менее 234 куб./ч.
Еще один параметр, который нужно учитывать, высчитывая расстояние между варочной поверхностью и воздухозаборником – площадь воздухозаборника. Его ширина не должна быть меньше ширины плитки.
По стандартам площадь воздухосборника должна быть больше или равна площади варочной поверхности
Общие рекомендации по установке
Обобщая подобные сведения, несложно указать нижние и верхние параметры.
- Вещать воздухозаборник над электрической плитой можно на расстоянии 65-75 см.
- А вот норма для газовой варочной поверхности с четырьмя конфорками – 75-90 см.
- Если монтаж вытяжки предполагает ее наклонное расположение, то допустимая норма низкой границы 55 см, высокой – 65 см. Выше поднимать прибор нельзя, так как он не сможет полностью охватывать и забирать весь загрязненный воздух.
Обратите внимание! Приведенные цифры – усредненные значения. Важно также учитывать и рост человека. Если человек высокий, можно вытяжку повесить и выше 90 см, но тогда придется приобрести более мощный прибор.
Где расположить розетку для вытяжки?
Решая вопрос о том, на какой высоте вешать вытяжку, важно заранее продумывать, где размещать розетку для нее. Здесь четких указаний нет, главное, чтобы доступ к такому техническому элементу был открытым и свободным.
Если описываемый прибор встраивается в мебель, розетку для него лучше устанавливать над шкафчиком на расстоянии 5 см от верхней планки фасада.
Обобщение по теме
Итак, отвечая на вопрос, на каком расстоянии от плиты должна устанавливаться вытяжка, специалисты обращают внимание на необходимость соблюдать существующие нормы, отвечающие безопасности эксплуатации обоих приборов. Любое отступление от правил сделает работу описываемой системы бесполезной. Любое снижение расположения способно будет привести к риску самовозгорания установки, к уменьшению уровня комфорта работы с варочной поверхностью.
На каком расстоянии вешать вытяжку от плиты
На какой высоте повесить вытяжку
Сложно представить любую кухню без вытяжки, ведь запахи от готовки пищи со временем впитываются в обои, мебель и шторы.
Это оборудование позволит сделать кухонное помещение более комфортным.
Но следует также позаботиться о правильной установке вытяжки, расположив ее на нужной высоте над плитой.
Это улучшит эстетический вид кухни и ее функциональность.
Виды кухонных вытяжек
Чтобы узнать высоту, на которую нужно вешать вытяжку, следует определиться с видом вытяжки.
Самое элементарное оборудование функционирует по принципу рециркуляции воздуха.
В данном случае воздух находится в пределах помещения, проходя через фильтры и возвращаясь обратно.
К таким приборам относятся подвесные или фильтрующие вытяжки.
Но это устройство не подключают к вентиляционной шахте.
К достоинствам данных систем относят современный дизайн, доступную стоимость, легкость монтажа и низкую степень шума.
Среди недостатков малый коэффициент полезного действия, поскольку рециркуляции обычно не хватает для очищения всей комнаты.
У обладателей остальных видов данного устройства, воздух выходит за пределы помещения.
Тогда кухонную вытяжку необходимо вывести на улицу либо в специальную вентиляционную шахту.
Этот прибор прикрепляют к стене или на сам потолок над варочной поверхностью.
Вентиляционные трубы можно скрыть от глаз, используя навесные шкафчики, которые позволят замаскировать их полностью или частично.
Также эти приборы требуют проведения сложных монтажных работ, хотя к ним прилагается не очень сложная инструкция.
В зависимости от типов установки приборы делятся на несколько видов:
Схема правильного размещения вытяжки
- Купольные вытяжки. Обладают наибольшей мощностью. Внешне похожи на зонтик и от него отходит труба;

Устройства купольного типа имеют несколько разновидностей:
- Каминные (пристенные). Их крепят на поверхность стены. По своей конструкции похожи на вентиляционные системы, используемые для каминов;
Расчет расстояния от плиты до вытяжки
Этот тип вытяжек крепят к потолку.
Оптимальная высота вытяжки
Узнать высоту установки определенной модели этого устройства, можно в инструкции.
Но это не всегда точный показатель, а примерный диапазон, в котором потребуется выбрать требуемое значение, зависимо от роста хозяйки и планировки кухни.
Можно также воспользоваться стандартами, в которых оговорено расстояние вытяжки до плиты.
Грамотную установку проводят с учетом вида варочной поверхности:
- в случае с электроплитой вытяжку вешают на 65-75 над ней;
- высота от газовой плиты до вытяжки составляет от 75 до 85 см.

Если приобретена наклонная вытяжка, то ее высота нижней части:
- от электрической плиты равна 35-45 см;
- от газовой плиты – 55-65 см.
Расстояние от вытяжки до плиты может изменяться в диапазоне этих 10 см в соответствии с мощностью оборудования для очищения воздуха.
Если устройство с низкой мощностью будет закреплено на максимальном расстоянии, то вряд ли оно будет качественно выполнять свою функцию.
Определяем высоту размещения вытяжки
В этом небольшом , вам расскажут, как правильно выбирать высоту для вытяжки. Приятного просмотра!
Разобравшись, на какой высоте следует располагать кухонную вытяжку, стоит узнать, с чем связаны такие стандарты.
Установив прибор на слишком маленькой высоте, придется испытывать трудности при готовке.
Посуда при этом будет нагреваться, особенно если она высокая.
Также при креплении вытяжки ниже установленных норм на нее будет попадать жир со сковородки.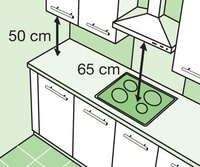
Не стоит забывать и о риске возникновения пожара, ведь прибор может задеть пламя зажженного газа.
Определяют расстояние от поверхности плиты от прибора, учитывая тип вытяжки, и проверяют наличие электропроводки в определенных точках.
Чаще всего установку вытяжки проводят после монтажа кухонной мебели, но необходимо заранее определиться с местом ее расположения.
В этом случае проводят розетку, размещая ее над прибором или над соседним кухонным шкафом.
Стоит учитывать, что обычно длина базового шнура бывает недостаточной для того, чтобы подключить вытяжку к уже установленным розеткам.
При выборе правильного места расположения вытяжки, нужно брать во внимание важные факторы, среди которых:
- мощность устройства;
- планировка и дизайн кухни;
- особенности варочной поверхности;
- значения, указанные в инструкции к прибору;
- стандарты, относящиеся к установке конкретного оборудования.
Обязательным критерием является рост готовящих.
Поэтому вытяжку устанавливают на такой высоте, чтобы хозяйка дотягивалась без труда до прибора, а он не мешал во время приготовления пищи.
Розетка для данного устройства, устанавливается на высоте 2-2,5 м.
Она должна находиться выше кухонных шкафов, в 10-30 см над их верхней частью.
Также стоит узнать будущее расположение воздуховода, который не должен закрывать розетку.
Поэтому ее нужно сместить на 20 см вправо либо влево от центра вытяжки.
Советы по установке вытяжек
Установка вытяжки на кухне является несложной процедурой.
Ее можно провести самостоятельно, но при недостаточном опыте лучше обратиться к профессиональным работникам.
За качество их работы отвечает салон кухни.
Если вытяжка была куплена в магазине бытовой техники, то ее могут установить специалисты из этого магазина.
И они тоже обещают гарантию качества.
Проще всего установить своими руками навесной прибор, работающий по типу рециркуляции.
Какие соковыжималки бывают для большого объёма яблок?
Не знаете? Данная статья. поможет вам разобраться в этом!
Читайте здесь. какой кухонный комбайн лучше всего выбрать.
Но предварительно нужно прочитать условия гарантийного обслуживания.
Сначала прибор прикладывают к стене и карандашом намечают его будущее расположение.
Если планируется замена кухонной мебели, то желательно обратить внимание на вытяжку, встраиваемую в подвесной шкаф.
Затем перфоратором сверлят стены под дюбель.
После этого вытяжку прикручивают к стене и готовят вентиляционный выход, очищая его от строительного мусора.
Гофру надевают на клапан и закрепляют при помощи силиконового герметика.
Свободный конец трубы помещают в шахту.
Затем надевают накладку, скрывающую гофру.
При выборе правильного расположения вытяжки на кухне нужно руководствоваться несколькими важными моментами.
К ним относятся мощность прибора, стандарты установки, данные в паспорте конкретного прибора.
Грамотная установка вытяжки на нужной высоте позволит избежать многих неприятных моментов, которые могут возникнуть при готовке пищи.
Учет правильной высоты прибора позволит избавить кухню частично либо полностью от неприятных запахов, остатков жира, сохранив в ней комфортную и приятную обстановку.
Также расположение вытяжки напрямую влияет на безопасность помещения – закрепив ее на нужной высоте, можно избежать риска возникновения пожара.
Так же советуем посмотреть
http://tehnosektor.ru
Какое расстояние необходимо от вытяжки до газовой плиты?
Хотя обычно в домах предусмотрена система вентиляции. Но зачастую она не справляется, должным образом со своими функциями, тем более в такой комнате, как кухня. Когда мы пользуемся газовой плитой, то мы можем столкнуться с неприятными запахами переработанного газа, но это не только неприятный, но и опасный для здоровья. В принципе на печи всегда происходят испарения, которые в себе несут определённые запахи и они будут впитываться в шторы и другие кухонные принадлежности.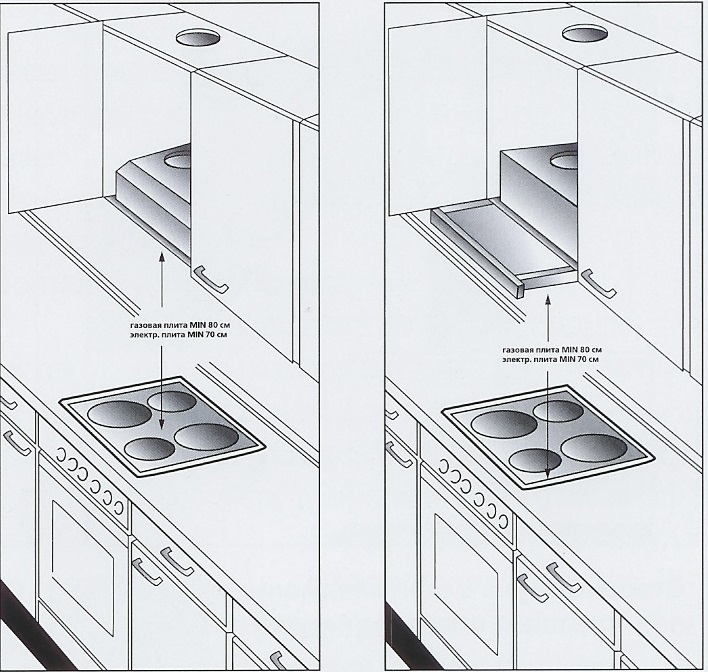 После чего нужно больше убирать в кухне, а соответственно тратить больше сил и времени.
После чего нужно больше убирать в кухне, а соответственно тратить больше сил и времени.
Как правильно установить вытяжку над газовой плитой
От правильно подобранной модели, будет зависеть экология вашего помещения и комфортабельность проведения времени на кухне.
Существует два вида вытяжных устройств
Начнем с первого вида устройства — это широко известный вид устройства с циркулярным встроенным угольным фильтром, который работает, по простому принципу рециркуляции воздуха. За счет этого воздух не выходит за пределы вашего помещения, а циркулирует, фильтруется и возвращается обратно в помещение. Эти устройства называют повседневными или фильтрующими.
Второй их вид, служит для отвода воздуха из помещения безвозвратно, это специальная вытяжка с принудительным забором нежелательного запаха и дыма. Для этого необходим вывод газовой вытяжки в вентиляционную шахту или на улицу. Вытяжка такого вида предусмотрена для большой кухни крупногабаритных размеров.
 Такой вид вытяжного устройства заметно выше и качественней, чем у циркулярной. Поэтому такие виды этого устройства, чаще всего устанавливают на кухнях. Тем более в большинстве многоэтажных домов, есть вентиляционные шахты, что упрощает установку такого оборудования.
Такой вид вытяжного устройства заметно выше и качественней, чем у циркулярной. Поэтому такие виды этого устройства, чаще всего устанавливают на кухнях. Тем более в большинстве многоэтажных домов, есть вентиляционные шахты, что упрощает установку такого оборудования.
Основные рекомендации по монтажу
На какой высоте вешать вытяжку? Высота вытяжки над газовой плитой должно быть не менее 65-70 сантиметров.
Размеры заборной части, желательно должны соответствовать размерам кухонной плиты.
Электрическая розетка должна размещаться в соответствующем месте над плитой и так, чтоб на неё не попадал жар от плиты.
Гофра труба, должна иметь по возможности минимальный изгиб, для хорошего прохождения воздуха. Тогда при включении механизма не будит потери КПД устройства.
Как повесить вытяжку?
Установка вытяжки с циркулярным фильтром не требует самых особых навыков или специального обучения и особых усилий. Для установки, нам потребуется обычный уровень. Как мы помним расстояние от вытяжки до плиты 65 — 70 см. Поэтому отмеряем нужную нам высоту и аккуратно чертим ровную линию. Затем отмеряем рулеткой расстояние от отверстия к отверстию для крепления, которые находятся на самой вытяжке. Переносим эти размеры на нашу линию, так чтоб она располагалась точно над плитой. Далее, перфоратором бурим отверстия. В отверстия вставляем пластиковые пробки и прикручиваем к ним наше оборудование.
Для установки, нам потребуется обычный уровень. Как мы помним расстояние от вытяжки до плиты 65 — 70 см. Поэтому отмеряем нужную нам высоту и аккуратно чертим ровную линию. Затем отмеряем рулеткой расстояние от отверстия к отверстию для крепления, которые находятся на самой вытяжке. Переносим эти размеры на нашу линию, так чтоб она располагалась точно над плитой. Далее, перфоратором бурим отверстия. В отверстия вставляем пластиковые пробки и прикручиваем к ним наше оборудование.
Некоторые решают прикрутить вытяжку к навесному шкафу. В таком случае мы, по такому же принципу, отмечаем на нужной нам высоте, куда прикрутить оборудование и крепим её саморезами по дереву.
Если вы устанавливаете вытяжку с принудительным отводом воздуха в вентиляционную шахту, то важно установить гофру или пластиковую трубу так, чтобы соединение конца трубы было крепким и без отверстий, чтобы не было потери КПД.
Принципиально важно, чтобы диаметр трубы соответствовал воздухозаборному отверстию в стене, для избежания потери качественной мощности откачки воздуха. После завершения процедуры установки оборудования, следует его протестировать в действии для проверки правильной установки вытяжки.
После завершения процедуры установки оборудования, следует его протестировать в действии для проверки правильной установки вытяжки.
Советы мастеров
В случае если вам при какой-то необходимости понадобится отдельная розетка для подключения вашего оборудования, то все подводящие к ней провода желательно спрятать в кабельный канал или в элементы кухонной гарнитуры. Возможно также скрыть в декоративных элементах отделки кухонного помещения.
Если на месте крепления у вас приклеена плитка, то будьте очень осторожны когда делаете отверстия, чтобы не разбить ее. Для этого лучше использовать специальные свёрла.
Заранее предусмотреть в линии электропитания срабатывающее устройство-автомат для аварийного отключения прибора, в случае перепада напряжения при аварийной ситуации.
Техническое обслуживание
Вне зависимости от того, какую вытяжку вы купите дорогую или дешевую, соответственно качественную или не очень, если её не обслуживать должным образом, то может произойти поломка деталей вентиляции. При таких поломках оборудование может продолжать работать, но происходит снижение КПД вентилируемой системы. Соответственно помещение не вентилируется должным образом, поэтому за возникшим вопросом «как монтировать вытяжку в кухонном помещении», следует вопрос «как ее правильно обслуживать?».
При таких поломках оборудование может продолжать работать, но происходит снижение КПД вентилируемой системы. Соответственно помещение не вентилируется должным образом, поэтому за возникшим вопросом «как монтировать вытяжку в кухонном помещении», следует вопрос «как ее правильно обслуживать?».
Если вытяжка имеет в своей конструкции встроенный угольный фильтр, то необходимо своевременно делать его замену. О сроках эксплуатации читайте на инструкции к фильтрам. Это является самым главным правилом для подвесных вытяжек, которые относятся к фильтрующим приборам. В данном случае фильтр является «сердцем» прибора. Поэтому следите за ним и регулярно его меняйте.
- Регулярно мойте вытяжку. На ней быстро скапливается гарь, жир и т. п.
- Следите за тем, чтобы крепление на трубе было прочным и не появлялось люфта на стыках трубы.
Искренне надеемся, что эта статья поможет разобраться вам как правильно смонтировать вытяжку, а также правильно эксплуатировать и обслуживать ее, чтобы насладиться свежим воздухом в вашей повседневной кухне.
Найти минимальное расстояние редактирования между заданными двумя строками
Алгоритм / идеи
Проблема не так сложна, как может показаться, когда мы разбиваем ее на более мелкие подзадачи и пытаемся их решить.
Пусть первая строка str1 длины ‘m’ будет «A1A2A3 … Am», где ‘A1’, ‘A2’ обозначают отдельные символы str1. Пусть вторая строка str2 длины ‘n’ будет «B1B2B3 … Bn». Чтобы вычислить расстояние редактирования между этими двумя строками, давайте начнем сравнивать последние символы str1 и str2.Если символ «Am» равен символу «Bn», то нам просто нужно вычислить расстояние редактирования между строками «A1A2A3 … Am-1» и «B1B2B3 … Bn-1». Но если символ «Am» не равен символу «Bn», тогда у нас есть следующие три варианта использования —
1. Вставить символ «Bn» в конец строки str1. Модифицированный str1 будет выглядеть как «A1A2A3 … AmBn». После этой операции мы можем начать вычислять расстояние редактирования между строками «A1A1A2 … Am» и «B1B2B3 … Bn-1», потому что нам не нужно учитывать последний символ «Bn» строки str2, который совпадает с вновь вставленным последний символ «Bn» в str1.Обратите внимание, как после выполнения операции вставки на str1 нам нужно учитывать первые символы «m» строки str1 и первые символы «n-1» строки str2 для вычисления расстояния редактирования.
2. Удалите последний символ «Am» строки str1 и вычислите расстояние редактирования между строками «A1A2A3 … Am-1» и «B1B2B3 … Bn». Обратите внимание, что после выполнения операции удаления для str2 нам нужно учитывать первые символы ‘m-1’ строки str1 и первые символы ‘n’ строки str2 для вычисления расстояния редактирования.
3. Замените последний символ «Am» строки str1 на символ «Bn».Теперь модифицированный str1 выглядит как «A1A2A3 … Am-1Bn», а str2 по-прежнему «B1B2B3 … Bn». После этой операции замены нам теперь нужно вычислить расстояние редактирования между строками «A1A2A3 … Am-1» и «B1B2B3 … Bn-1». Обратите внимание, что после выполнения операции подстановки на str1 теперь нам нужно учитывать первые символы ‘m-1’ строки str1 и первые символы ‘n-1’ строки str2 для вычисления расстояния редактирования.
Как решить, какой из этих трех вариантов использовать? Что ж, мы не можем решить это заранее, и нам нужно опробовать все три варианта и использовать результат выбора, который дает нам минимальное расстояние редактирования.
Если мы хотим выразить вышеуказанные шаги в вызове функции findEditDistance (String str1, String str2, int m, int n), то эта функция будет выглядеть следующим образом:
Теперь, как вы можете заметить, эта функция является рекурсивной. в природе, и поэтому нам нужно определить базовый случай для этой рекурсии.
Базовый случай —
1. Если длина str1 равна 0, то нам нужно вставить все символы str2 в str1, чтобы сделать их равными. Следовательно, расстояние редактирования между str1 и str2, когда str1 пусто, равно длине str2.п) алгоритм.
Подход динамического программирования: Теперь давайте посмотрим, как мы можем оптимизировать временную сложность этого алгоритма. Дерево частичной рекурсии последовательности вызовов для функции findDistance (String str1, String str2, int m, int n) будет выглядеть следующим образом —
Как указано выше, существуют вызовы функций с одинаковыми аргументами, которые вычисляются снова и снова. Чтобы избежать этих избыточных вычислений, мы используем подход, основанный на динамическом программировании.
В этом методе мы используем восходящий подход для вычисления расстояния редактирования между str1 и str2.Мы начинаем с вычисления расстояния редактирования для более мелких подзадач и используем результаты этих более мелких подзадач для вычисления результатов для последующих более крупных задач. Результаты сохраняются в двумерном массиве, как показано ниже.
Каждая ячейка (m, n) этого массива представляет расстояние между первыми символами «m» строки str1 и первыми символами «n» строки str2. Например, когда ‘m’ равно 0, расстояние между str1, имеющим длину 0, и str2 длины ‘n’, равно ‘n’. Обратите внимание на 0-ю строку вышеприведенной матрицы. То же самое и для значений в 0-м столбце, где длина str2 равна 0.
Теперь в этой матрице для ячейки (m, n), которая представляет расстояние между str1 длиной ‘m’ символов и str2 длиной ‘n’ символов, если ‘m’-й символ str1 и’ n’-й символ str2 одинаковы, тогда нам просто нужно заполнить ячейку (m, n), используя значение ячейки (m-1, n-1), которое представляет расстояние редактирования между первыми символами ‘m-1’, если str1 и первые символы ‘n-1’ ул. 2. Обратите внимание на красные стрелки в приведенном выше массиве.
Если m-й символ str1 не равен n-му символу str2, то мы выбираем минимальное значение из следующих трех случаев —
1.Удалите m-й символ строки str1 и вычислите расстояние редактирования между символами m-1 строки str1 и символами n строки str2. Для этого вычисления нам просто нужно сделать — (1 + array [m-1] [n]), где 1 — стоимость операции удаления, а array [m-1] [n] — это расстояние редактирования между ‘m-1’ символы str1 и символы ‘n’ str2.
2. Аналогично, для второго случая вставки последнего символа str2 в str1 мы должны сделать — (1 + array [m] [n-1]).
3. И для третьего случая замены последнего символа str1 последним символом str2 мы используем — (1 + array [m-1] [n-1]).
Пожалуйста, проверьте функцию findDistance (String str1, String str2) во фрагменте кода для получения подробной информации о реализации. Временная и пространственная сложность этого метода составляет O (mn), где m — длина str1, а n — длина str2.
Пожалуйста, добавьте комментарии ниже, если у вас есть отзывы / вопросы.
Измерение расстояния на карте
Инструмент измерения расстояния — это простой способ найти расстояние между двумя или более точками на карте.
Выберите скорость…
Или выберите вид транспорта …
Как использовать инструмент измерения расстояния
Просто щелкните один раз в одной точке, затем нажмите еще раз во второй точке. Затем должно отображаться расстояние. Вы можете щелкнуть более двух точек, чтобы построить непрерывный маршрут.
Используйте переключатель миль / км / морских миль / ярдов для измерения расстояний в км, милях или морских милях. Параметр «Автопанорамирование» перемещает карту при щелчке по точкам.
Текстовое поле «Поиск местоположения» позволяет быстро добраться до нужной области, не тратя время на масштабирование и панорамирование, чтобы найти ее.Например, если вы хотите найти город Рим в Италии, введите «Рим, Италия», а затем нажмите «Поиск». Затем карта переместится прямо в Рим. Обратите внимание на формат «[город] [запятая] [пробел] [округ]».
Переключить маркеры — показать или скрыть маркеры, если они мешают.
Очистить последнюю удаляет последнюю точку с карты
Увеличить по размеру — масштабирование и панорамирование карты для наилучшего соответствия всех ваших точек при максимально возможном увеличении.
Очистить карту — это кнопка сброса, которая очищает все точки и позволяет снова начать измерение расстояния.
Вы можете редактировать положение любых существующих точек, перетаскивая маркер (когда они отображаются) и оставляя маркер в его новом положении
Вы также можете настроить высоту карты, сделав ее большим, средним или маленьким.
Вы можете удалить точку, щелкнув узел правой кнопкой мыши.
Будущие идеи и улучшения
- Автоматическое изменение маршрута для оптимального расстояния (задача коммивояжера)
- Есть другие скорости, например оптоволоконный кабель (~.6 c) и Маха
- Возможность добавления заголовка к маркеру, который затем появляется при наведении курсора мыши и экспорте данных
История версий
- 6th Julty 2020 — Новая опция экспорта ссылки на маршрут. Находится в разделе параметров экспорта
- 2 июня 2019 — Исправлена ошибка, из-за которой не работал вывод счетчиков
- 29 мая 2019 — Реализованы листовки-карты
- 20 мая 2019 г. — Исправлена ошибка в браузере IE
- 9 мая 2019 г. — Исправлена ошибка, из-за которой расстояние не сбрасывалось до нуля при нажатии кнопки «Очистить карту».
- 14 сентября 2017 г. — Расстояние теперь отображается на карте в полноэкранном режиме
- 4 августа 2017 — Переключатель единиц измерения обновлен.Футов добавлено
- 24 июля 2017 — Полноэкранный режим перенесен на карту. Теперь находится в правом верхнем углу
- , 4 июля 2017 г. — Исправлена проблема с экспортом в CSV и XLSX
- 29 января 2017 г. — Возможность отображения карты высот и экспорта файла CSV с данными о высоте вдоль маршрута
- 25 ноября 2016 г. — экспорт KML для отображения контактов на каждом узле маршрута
- 23 ноября 2016 г. — добавлена опция загрузки KML, CSV и XLSX
- 19 июля 2016 г. — Исправлены ошибки, связанные с изменением вида транспорта и расчетного времени в пути при изменении единиц измерения
- 5 июля 2016 — Добавлены метры как единицы расстояния
- 25 июня 2016 — Единицы скорости движения меняются в зависимости от единиц расстояния
- 20 июня 2016 г. — Исправлена ошибка, из-за которой количество дней отображалось в два раза больше фактического значения
- 24 марта 2016 — Точки маршрута теперь можно добавлять в середине пути.Очки также можно удалить, щелкнув правой кнопкой мыши
- 25 января 2016 г. — Скорость теперь можно вводить вручную
- 28 декабря 2015 г. — Добавлена возможность переключения между минутами, часами и днями для оценки времени в пути
- 24 июня 2014 — Добавлена опция привязки к дорогам
- 24 марта 2014 г. — Добавлена опция «Панорама до моего местоположения»
- 11 января 2012 г. — Реализован Google Maps API V3. Добавлен полноэкранный режим
- 12 октября 2010 г. — маркеры теперь показывают их широту и долготу при наведении на них курсора
- 15 октября 2009 г. — Добавлен вывод времени в пути
- 12 октября 2009 г. — Добавлена опция карты местности
- 20 февраля 2008 г. — Обновленный дизайн теперь с перетаскиваемыми маркерами
- 1 ноября 2007 г. — Добавлено текстовое поле быстрого поиска
- 19 октября 2007 г. — Ярды добавлены в качестве единицы измерения
- 9 октября 2007 г. — добавлены морские мили в качестве единицы измерения
- 5 сентября 2007 г. — обновлен описательный текст
- 28 июня 2007 г. — Страница создана
Соответствующие ссылки
Если вы пытаетесь измерить расстояние между двумя городами, то инструмент «Как далеко между ними», вероятно, больше подходит для ваших нужд.
Расстояние— PyMOLWiki
Расстояние создает новый объект расстояния между двумя выделениями. Он отобразит все расстояния в пределах отсечки. Расстояние также используется для образования водородных связей. Расстояние вызова без аргументов покажет расстояния между выделениями (pk1) и (pk1), которые можно установить в режиме редактирования или с помощью действия мыши PkAt (обычно при нажатии средней клавиши CTRL). Примечание. Для интерактивного использования мастер измерения (из меню PyMOL) упрощает измерение расстояний, чем использование команды расстояния. |
расстояние [имя [, выбор1 [, выбор2 [, отсечка [, режим]]]]]
наименование
- строка: имя объекта расстояния для создания
selection1
- строка: выбор первого атома
выбор2
- строка: выбор второго атома
отсечка
- float: наибольшее расстояние для отображения
режим
- 0: все межатомные расстояния
- 1: только межсоединения
- 2: показывать только полярные контактные расстояния
- 3: аналогично mode = 0, но использовать параметр distance_exclusion
- 4: расстояние между центроидами ( новых в 1.8,2 )
cmd.distance (имя строки, выделение строки1, выделение строки2,
отсечка с плавающей запятой, режим int)
# возвращает среднее расстояние между всеми атомами / кадрами
ПРИМЕРЫ
- Получите и покажите расстояние от альфа-углерода остатка 10 до альфа-углерода остатка 40 в 1ESR:
# сделать первый остаток 0. zero_residues 1esr, 0 расстояние i. 10 и п. CA, я. 40 и п. CA
- Получить и показать расстояние от альфа-углерода остатка 10 до альфа-углерода остатка 35-42 в 1ESR:
# сделать первый остаток 0.zero_residues 1esr, 0 расстояние i. 10 и п. CA, я. 35-42 и п. CA
- Этот аккуратный пример показывает, как измерять расстояние от атома в молекуле до всех других атомов в молекуле (поскольку PyMol поддерживает подстановочные знаки).
cmd.distance ("(/ mol1 /// 1 / C)", "(/ mol1 /// 2 / C *)")
или написано без кода PyMolScript,
расст / моль1 /// 1 / C, / моль1 /// 2 / C *
- Создание нескольких объектов расстояния
для at1 в cmd.index ("resi 10"): \
для at2 в cmd.index ("resi 11"): \
cmd.distance (Нет, "% s`% d"% at1, "% s`% d"% at2)
расстояние (выбор1), (выбор2) # пример dist i. 158 и п. CA, я. 160 и п. CA дистанция mydist, 14 / CA, 29 / CA расстояние hbonds, all, all, 3.2, mode = 2
Максимальные и минимальные значения — подход к исчислению
10
Поворотные точки графика
МЫ ГОВОРЯЕМ, ЧТО ФУНКЦИЯ f ( x ) имеет относительное максимальное значение x = a ,
, если f ( a ) на больше , чем любое значение, непосредственно предшествующее или последующее.
Мы называем это «относительным» максимумом, потому что другие значения функции на самом деле могут быть больше.
Мы говорим, что функция f ( x ) имеет относительное минимальное значение x = b ,
, если f ( b ) на меньше , чем любое значение, непосредственно предшествующее или последующее.
Опять же, другие значения функции могут быть меньше. С таким пониманием мы откажемся от термина «относительный».
Значение функции, значение y , максимальное или минимальное, называется экстремальным значением.
Теперь, что характеризует график при экстремальном значении?
Касательная к кривой горизонтальна . Мы видим это в точках A и B . Наклон каждой касательной линии — производная при оценке на a или b — равен 0.
f ‘ ( x ) = 0.
Более того, в точках непосредственно к слева от от максимума — в точке C — наклон касательной положительный: f ‘ ( x )> 0. В то время как в точках непосредственно к справа — в точке D — наклон отрицательный: f ‘ ( x )
Другими словами, максимум f ‘ ( x ) меняет знак с + на -.
Как минимум, f ‘ ( x ) меняет знак с — на +. Мы видим, что в точках E и F .
Мы также можем заметить, что максимум при A график вогнут вниз. (Тема 14 Precalculus.) Хотя, как минимум, на B , она вогнута вверх.
Значение x , при котором функция имеет максимум или минимум, называется критическим значением.На рисунке —
— критические значения x = a и x = b .
Критические значения определяют точки поворота, в которых касательная параллельна оси x . Критические значения — если таковые имеются — будут решениями от до f ‘ ( x ) = 0.
Пример 1. Пусть f ( x ) = x 2 — 6 x + 5.
Есть ли критические значения — какие-нибудь поворотные моменты? Если да, то определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума?
Решение . f ‘ ( x ) = 2 x — 6 = 0 подразумевает x = 3. (Урок 9 алгебры)
x = 3 — единственное критическое значение. Это x — координата поворотной точки.Чтобы определить y -координат, оцените f при этом критическом значении — оцените f (3):
| f ( x ) | = | x 2 — 6 x + 5 |
| f (3) | = | 3 2 — 6 · 3 + 5 |
| = | −4. | |
Крайнее значение — 4. Чтобы увидеть, является ли он максимумом или минимумом, в этом случае мы можем просто посмотреть на график.
f ( x ) — парабола, и мы видим, что точка поворота минимальна.
Найдя значение x , где производная равна 0, мы обнаружили, что вершина параболы находится в точке (3, −4).
Но мы не всегда сможем посмотреть на график.Алгебраическим условием минимума является то, что f ‘ ( x ) меняет знак с — на +. Мы видим это в точках E , B , F выше. Величина наклона увеличивается.
Теперь сказать, что наклон увеличивается, значит сказать, что при критическом значении вторая производная (Урок 9) — скорость изменения наклона — равна положительному значению .
Опять же, вот f ( x ):
| f ( x ) | = | x 2 — 6 x + 5. |
| f ‘ ( x ) | = | 2 x — 6. |
| f » ( x ) | = | 2. |
f » при критическом значении 3 — f » (3) = 2 — положительно. Это алгебраически говорит нам, что критическое значение 3 определяет минимум.
Достаточные условия
Теперь мы можем сформулировать эти достаточные условия для экстремальных значений функции при критическом значении a :
Функция имеет минимальное значение x = a , если f ‘ ( a ) = 0
и f’ ‘ ( a ) = положительное число.
Функция имеет максимальное значение x = a , если f ‘ ( a ) = 0,
и f’ ‘ ( a ) = отрицательное число.
В случае максимума наклон касательной равен , при уменьшении — от положительного до отрицательного. Мы видим, что в точках C , A , D .
Пример 2. Пусть f ( x ) = 2 x 3 — 9 x 2 + 12 x — 3.
Есть ли крайние значения? Во-первых, существуют ли какие-либо критические значения — решения для f ‘ ( x ) = 0 — и определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума? Где поворотные моменты?
| Решение . f ‘ ( x ) = 6 x 2 -18 x + 12 | = | 6 ( x 2 — 3 x + 2) |
| = | 6 ( x — 1) ( x — 2) | |
| = | 0 | |
означает:
x = 1 или x = 2.
(Урок алгебры 37.)
Это критические значения. Каждый определяет максимум или минимум? Чтобы ответить, мы должны оценить вторую производную для каждого значения.
| f ‘ ( x ) | = | 6 x 2 -18 x + 12. |
| f » ( x ) | = | 12 x — 18. |
| f » (1) | = | 12-18 = −6. |
Вторая производная отрицательна. Таким образом, функция имеет максимум x = 1.
Чтобы найти y -coördinate — экстремальное значение — на этом максимуме мы оцениваем f (1):
| f ( x ) | = | 2 x 3 — 9 x 2 + 12 x — 3 |
| f (1) | = | 2–9 + 12–3 |
| = | 2. | |
Максимум происходит в точке (1, 2).
Затем, x = 2 определяет максимум или минимум?
| f ‘ ( x ) | = | 12 x — 18. |
| f » (2) | = | 24–18 = 6. |
Вторая производная положительна.Следовательно, функция имеет минимум x = 2.
Чтобы найти y -coördinate — крайнее значение — на этом минимуме, мы оцениваем f (2):
| f ( x ) | = | 2 x 3 — 9 x 2 + 12 x — 3. |
| f (2) | = | 16–36 + 24–3 |
| = | 1. | |
Минимум находится в точке (2, 1).
Вот собственно график f ( x ):
Решения для f » ( x ) = 0 указывают точку перегиба в этих решениях, а не максимум или минимум. Пример: y = x 3 . y » = 6 x = 0 подразумевает x = 0. Но x = 0 — точка перегиба на графике y = x 3 , а не максимум или минимум .
Другой пример: y = sin x . Решения y » = 0 — это умножения числа π, которые являются точками перегиба.
Задача 1. Найти координаты вершины параболы,
y = x 2 — 8 x + 1.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
y ‘ = 2 x — 8 = 0.
Это подразумевает x = 4. Это x -кординат вершины. Чтобы найти y -кординат, оцените y при x = 4:
y = 4 2 — 8 · 4 + 1 = −15.
Вершина находится в точке (4, −15).
Задача 2. Проверьте каждую функцию на наличие максимумов и минимумов.
a) y = x 3 — 3 x 2 + 2.
y ‘ = 3 x 2 — 6 x = 3 x ( x — 2) = 0 означает
x = 0 или x = 2.
y ‘ ( x ) = 6 x — 6.
у » (0) = −6.
Вторая производная отрицательна. Это означает, что существует максимум x = 0. Это максимальное значение составляет
.y (0) = 2.
Далее,
y ‘ (2) = 12 — 6 = 6.
Вторая производная положительна. Это означает, что существует минимум x = 2.Это минимальное значение
.y (2) = 2 3 — 3 · 2 2 + 2 = 8-12 + 2 = −2.
б) y = −2 x 3 — 3 x 2 + 12 x + 10.
При x = 1 получается максимум y = 17.
При x = −2 минимум y = −10.
c) y = 2 x 3 + 3 x 2 + 12 x — 4.
Поскольку f ‘ ( x ) = 0 не имеет реальных решений, нет и экстремальных значений.
d) y = 3 x 4 — 4 x 3 — 12 x 2 + 2.
При x = 0 получается максимум y = 2.
При x = −1 минимум y = −3.
При x = 2 минимум y = −30.
Следующий урок: Применение максимальных и минимальных значений
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.com
Инструкции по анализу ШАГ 1: a. Используйте метрическую линейку, чтобы измерить минимальное расстояние в миллиметрах между вершинами гор. б. На основании этих измерений
Презентация на тему: «Инструкции по анализу, ШАГ 1: a. Используйте метрическую линейку для измерения минимального расстояния в миллиметрах между вершинами гор. B. На основании этих измерений», — стенограмма презентации:
1 Инструкции по анализу ШАГ 1: a.Используйте метрическую линейку, чтобы измерить минимальное расстояние в миллиметрах между вершинами гор. б. Основываясь на этих измерениях, спрогнозируйте, какие популяции будут иметь самый высокий уровень скрещивания. ШАГ 2: Затем, используя генетические данные (стрелки), нарисуйте двуглавые стрелки, чтобы соединить популяции, чтобы обозначить фактический уровень размножения между популяциями. Чем больше стрелок, тем больше связи, т.е. больше разведения; меньшее количество стрелок означает меньшую связь, т.е. меньшее разведение. ШАГ 3: а. Ответьте на вопросы, чтобы сравнить свои результаты с шага 1 и шага 2.б. Предскажите, где проходят автомагистрали, нарисовав их на карте.
2 ШАГ 1: 1. С помощью метрической линейки измерьте минимальное расстояние в миллиметрах между вершинами гор. 2. На основании этих измерений спрогнозируйте, в каких популяциях будет самый высокий уровень скрещивания.
3 ШАГ 2: Используя генетические данные (стрелки), нарисуйте двуглавые стрелки, чтобы соединить популяции, чтобы обозначить фактический уровень размножения между популяциями.Чем больше стрелок, тем больше связи, т.е. больше разведения; меньшее количество стрелок означает меньшую связь, т.е. меньшее разведение.
4 ШАГ 2: Используя генетические данные (стрелки), нарисуйте двуглавые стрелки, чтобы соединить популяции, чтобы обозначить фактический уровень размножения между популяциями.

 При такой комбинации ширина столешницы должна быть не менее 90 см.
При такой комбинации ширина столешницы должна быть не менее 90 см.
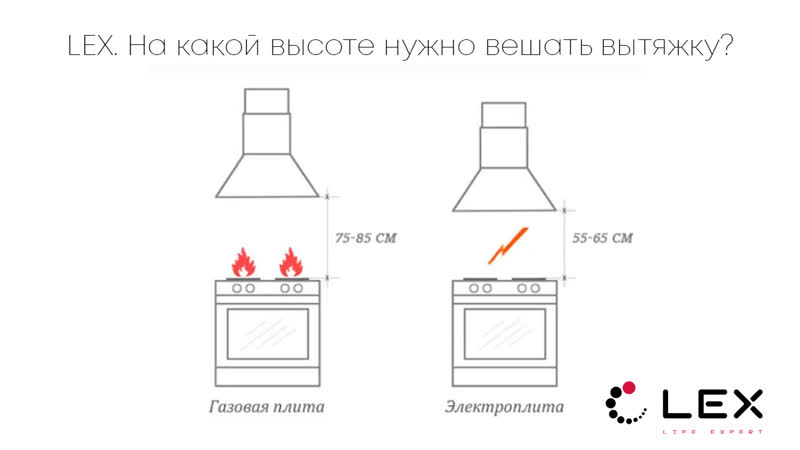 Такой вид вытяжного устройства заметно выше и качественней, чем у циркулярной. Поэтому такие виды этого устройства, чаще всего устанавливают на кухнях. Тем более в большинстве многоэтажных домов, есть вентиляционные шахты, что упрощает установку такого оборудования.
Такой вид вытяжного устройства заметно выше и качественней, чем у циркулярной. Поэтому такие виды этого устройства, чаще всего устанавливают на кухнях. Тем более в большинстве многоэтажных домов, есть вентиляционные шахты, что упрощает установку такого оборудования.