Пластичность бетона таблица: Подвижность бетонной смеси по маркам с таблицей, способы определения
Определение подвижности бетонной смеси
Текучесть (подвижность) бетонной смеси является одним из основных факторов, которые влияют на формование материала в опалубке, и определяется соотношением главных компонентов смеси, наличием добавок-пластификаторов, количеством воды и качеством бетона.
Подвижность определяется как опытным путем, исходя из состава и размера частиц наполнителей, так и экспериментальным — с помощью лабораторных испытаний и измерения в формах.
Подвижность смеси из бетона.
Удобоукладываемость бетонного раствора: что это такое
Бетонный камень — прочный строительный материал, продукт реакций гидратации, протекающих в водном растворе цемента. Дополнительно в состав могут быть добавлены заполняющие компоненты:
- песок;
- щебень;
- гравий.
Количество воды в составе бетонного раствора может быть разным.
Важно!
Показывает количество воды в составе бетонного теста водоцементное соотношение.
Обычное значение в/ц, как правило, 0,3—0,55. Для реакции гидратации достаточно в/ц менее 0,3, но смесь получается очень густой.
Удобоукладываемость бетона зависит от двух параметров:
- подвижность;
- расслаиваемость.
Подвижность — что это такое
Основным технологическим параметром свежей бетонной смеси является удобоукладываемость — способность раствора заполнять опалубку и принимать ее форму, не теряя однородности и монолитности.
Формуемость влияет не только на скорость работы с материалом на стройплощадке, но и на его конструктивные характеристики. При высокой вязкости в бетоне будут образовываться пустоты и поры, а при сильной текучести — будет снижена прочность конструкции.
Удобоукладываемость зависит от способности смеси деформироваться без изменения структуры (пластичности) и склонности к растеканию под собственным весом (подвижности). За счет двухфазной структуры — матрицы из цементного теста и наполнителей — свежий бетон образует вязкую массу, которая одновременно проявляет свойства твердого и жидкого тела.
При большом содержании воды в цементном тесте матрица будет иметь аморфную структуру. Связей, которые будут образованы при гидратации цемента, окажется недостаточно для обеспечения нужной вязкости. Водянистая смесь будет хорошо заполнять емкость и растекаться по поверхности.
Большое количество наполнителя сделает раствор неподатливым, малоподвижным и жестким. Жесткость бетона определяется не только содержанием частиц наполнителя (песок, гравий и др.), но и их дисперсностью.
Чем мельче частицы, тем больше площадь их поверхности, которая обволакивается цементным тестом. Процессы адгезии на границе матрица-частица удерживают бетонную смесь от растекания.
Если в разведенный цемент добавить наполнитель со слишком крупными частицами, то сил адгезии не хватит для удержания вязко-жидкой структуры в стабильной форме. Жидкая основа будет относительно свободно растекаться между частицами наполнителя, что негативно повлияет на однородность бетона.
Жесткие бетонные растворы являются наиболее выгодными для застройщиков, т. к. позволяют добавить пыль и некондиционный мелкий наполнитель. Это позволяет сэкономить на дорогом цементе, но сказывается на свойствах будущей конструкции. Чтобы получить заданную прочность, перед заливкой опалубки бетонщик проверяет подвижность смеси.
к. позволяют добавить пыль и некондиционный мелкий наполнитель. Это позволяет сэкономить на дорогом цементе, но сказывается на свойствах будущей конструкции. Чтобы получить заданную прочность, перед заливкой опалубки бетонщик проверяет подвижность смеси.
Как определяют подвижность бетонной смеси
Для определения текучести бетона используют метод испытания с конусом Абрамса, который также называется «испытанием бетона на осадку».
Этот метод используется в отечественной практике и соответствует европейским нормам.
Видео: Конус Абрамса
Требования к конусу
Конус Абрамса изготавливают из листовой стали не менее 1,5 мм толщиной. Его внутренняя поверхность имеет шероховатость не более 40 мкм. Есть два вида конуса: нормальный и увеличенный.
Нормальный конус используют для растворов, содержащих заполнители фракции не более 40 мм. Для смесей с более крупным заполнителем применяется увеличенный конус.
Как проводится испытание бетона на осадку
Перед проведением испытаний внутреннюю поверхность конуса очищают и смачивают.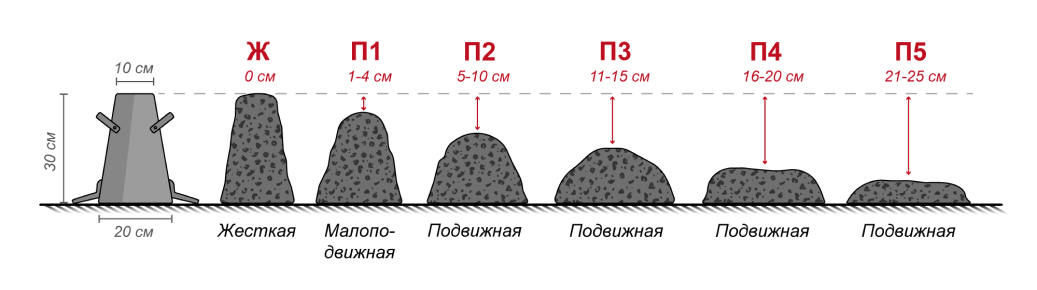
Конус устанавливают на металлический лист и заполняют его бетонной смесью с помощью воронки. Смесь закладывается в 3 слоя (для марок П1—П3), причем каждый слой уплотняется штыкованием при помощи металлического стержня 25 раз (в увеличенном конусе — по 56 раз для каждого слоя). Для марок П4—П5 конус заполняется в один прием, а штыкование применяется 10 раз в конусе нормального размера или 20 — в увеличенном.
Когда смесь уложена и уплотнена, излишек срезают кельмой по верхней кромке и, не позднее, чем через 3 минуты плавно снимают конус (в течение 5—7 секунд).
Затем измеряют осадку конуса бетона и сравнивают с высотой металлического конуса. Для увеличенного конуса значение умножают на 0,67.
Видео: Учимся определять подвижность бетона
Нормы и обозначение
Посмотреть «ГОСТ 7473–2010» или
Подвижность строительной смеси указывается производителем и обозначает класс, к которому относится раствор.
Подвижность бетона определяется производителем. Характеристика имеет обозначение в виде буквы «П» с цифрой. Число указывает класс, к которому относится смесь. Согласно ГОСТу 7473—2010, выделяют такие параметры:
Характеристика имеет обозначение в виде буквы «П» с цифрой. Число указывает класс, к которому относится смесь. Согласно ГОСТу 7473—2010, выделяют такие параметры:
- П1. Означает осадку раствора до 4 см. Состав с таким свойством называется «сухой бетон» и практически не используется в стройке.
- П2. Осадка смеси до 9 сантиметров. Марка бетона относится к полусухому типу.
- Состав со значением П3. Оседает на глубину до 15 см. Этот класс бетона широко применяют во всех видах внешних работ или внутри дома.
- Марка по удобоукладываемости П4. Характеризуется подвижностью до 20 сантиметров. Используется для фундамента монолитного типа.
- Пластичный материал со значением П5. Оседает до 25 см. Подвижность бетона с более высоким коэффициентом не гарантирует долговечности строения.
Таблица подвижности по удобоукладываемости:
Факторы, влияющие на подвижность
Представим себе бетонные растворы с разным содержанием воды. Густой раствор с низким водоцементным соотношением держит форму и не растекается.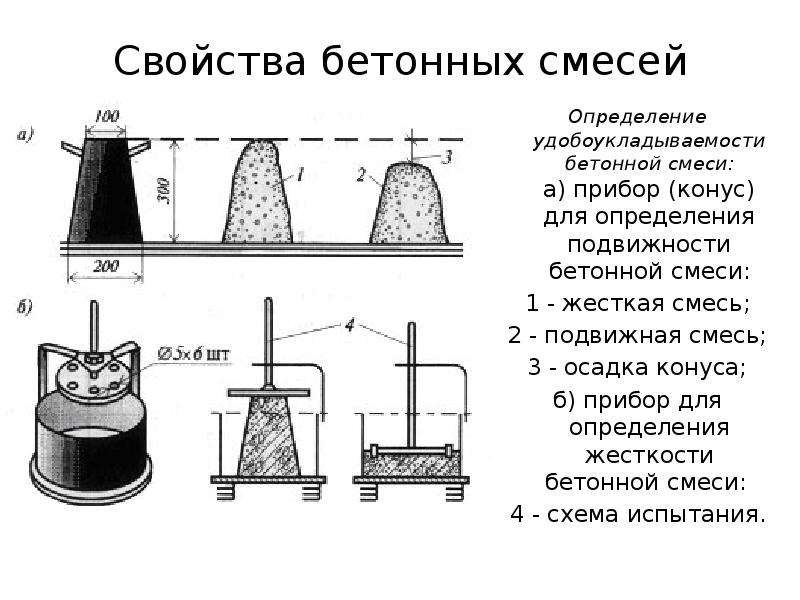 Чем выше водоцементное соотношение, тем выше текучесть раствора. Таким образом, основной фактор, влияющий на подвижность бетонной смеси — пропорции воды к цементу.
Чем выше водоцементное соотношение, тем выше текучесть раствора. Таким образом, основной фактор, влияющий на подвижность бетонной смеси — пропорции воды к цементу.
Но чем больше в растворе воды, тем меньше прочность готовой конструкции.
Казалось бы, выход – уменьшить количество воды в смеси, но густые растворы тяжело заполняют опалубку, особенно, если конструкция густо армирована. Требуется приложить много усилий и затрат электроэнергии на уплотнение бетонной смеси в опалубке; в противном случае, в готовой конструкции будут пустоты, что снизит ее прочность.
Подвижность бетонной смеси зависит также от следующих факторов:
- Вид цемента. Портландцемент, содержащий кремнеземистые компоненты, позволяет получить более подвижные смеси.
- Размер и форма заполняющих материалов. Крупные заполнители увеличивают подвижность бетона.
- Наличие примесей в песке. Примесь глины снижает текучесть цементной смеси.
В настоящее время существует простой, экономически целесообразный и эффективный метод повышения подвижности бетона без снижения его прочностных характеристик. Это применение пластификаторов.
Это применение пластификаторов.
В качестве пластифицирующих добавок используют:
- хлористые соли;
- электролиты;
- поверхностно-активные вещества;
- клей ПВА-МБ;
- известь (для штукатурных цементных растворов).
У каждого из этих видов добавок есть свои ограничения, кроме того, не всегда возможно точно подобрать дозировку и рассчитать эффект.
Чтобы получить гарантированный результат, применяют пластификаторы промышленного производства, которые могут поставляться как в форме порошка, так и в форме жидкости, удобной для дозирования и добавления в раствор.
Пластифицирующие добавки подразделяются на 4 группы в зависимости от силы воздействия на бетонный раствор.
Помимо увеличения пластичности, применение пластификаторов обеспечивает дополнительные преимущества:
- Экономия цемента. Например, пластификаторы CEMMIX Plastix и CemPlast позволяют экономить до 10—15% цемента.
- Экономия воды.
- Улучшение смешиваемости раствора.

- Предотвращение расслаивания смеси.
- Увеличение срока «жизни» раствора, что может быть важно при необходимости транспортировки.
- Качественное заполнение опалубки.
- Самоуплотнение смеси, благодаря чему можно уменьшить затраты на ее обработку.
- Более быстрый набор прочности (например, раствор с добавкой для теплых полов CemThermo показывает марочную прочность бетона уже на 10-й день, то есть прочность через 28 суток будет выше расчетной).
- Улучшение сцепления с арматурой.
Пластификаторы испытаны в лаборатории, их точная дозировка рассчитана. Они не оказывают негативного влияния на арматуру и не провоцируют появление высолов на поверхности бетона.
Как определить подвижность?
Применяются различные методы, определяющие подвижность бетонной смеси, которые различаются сложностью получения результатов. Осадка конуса — самый быстрый метод. В соответствии с ним определяется, насколько естественным образом (под своим весом) усаживается бетонный раствор, предварительно сформированный в конус. Используется конусообразная металлическая форма, размеры которой зависят от величины фракций щебня. К примеру, конструкция высотой 300 мм, малым диаметром 100 мм и большим — 300 мм, внутренним объемом 7 л.
Используется конусообразная металлическая форма, размеры которой зависят от величины фракций щебня. К примеру, конструкция высотой 300 мм, малым диаметром 100 мм и большим — 300 мм, внутренним объемом 7 л.
В нее с широкой стороны тремя порциями укладывают бетонную композицию, каждый слой которой уплотняют путем штыкования (8 – 9 движений на один слой) гладкой арматурой. Лишний раствор убирают. Затем конус переворачивают, как детскую паску, и освобождают раствор, уложенный конусом. Далее дают время, чтобы смесь осела, и осуществляют проверки величины подвижности вычислением снижения высоты раствора относительно верхнего среза формы (высота 300 мм), в которой он находился. Проверка проводится несколько раз для получения усредненного (более точного) результата.
Отсутствие разницы сообщает о максимальной жесткости состава. Когда смесью набрана разница высот до 150 мм — это малоподвижная композиция. Снижение конусом высоты до 150 мм и больше характеризует раствор как максимально текучий (подвижный).
Еще один метод — испытания вискозиметром (используется, когда в смесях щебень имеет размеры 0,5 – 4 см). Конусообразная форма раствора (формируется аналогично описанному выше) ставится на вибростол. В нее втыкается штатив с делениями, на который сверху надевается металлический диск. Включается виброплита и секундомер. Засекается время, когда груз под действием вибрации опустится вдоль штатива до определенной отметки. Полученная величина времени умножается на постоянный коэффициент 0,45. В результате определяется подвижность состава.
Следующий метод — испытания в формах. Используется открытый с одной стороны металлический куб (к примеру, 200 х 200 х 200 мм) для композиций с фракциями щебня до 7 см. В нем размещается конусообразная масса бетона.
Далее куб устанавливается на виброплиту. Одновременно с плитой включается секундомер. Измеряется интервал времени, за которое испытуемые бетонные смеси заполнят углы формы, а поверхность раствора становится ровной. Полученное время умножается на коэффициент 0,7. Результат — оценка подвижности состава.
Результат — оценка подвижности состава.
Вернуться к оглавлению
Как применяются в строительстве смеси разной подвижности
Подвижные смеси классифицируются на 4 категории, с П1 по П5:
- П1 — малоподвижные. Наиболее густые смеси. Используются для монолитных конструкций (например, лестниц). Обязательно применяется механическое уплотнение бетонной смеси.
- П2—П3 используются часто, подходят для большинства стандартных конструкций. Подвергаются уплотнению.
- П4 применяются для армированных конструкций, например, колонн, высоких фундаментов. Не требуют уплотнения.
- П5 — текучие смеси (литьевые) применяются только в герметичных опалубках. Подходят для густоармированных конструкций.
Способы определения
Определение подвижности бетонной смеси может проводиться как непосредственно на площадке, так и в лабораторных условиях.
Определение эластичности конусом
Наиболее простой и часто применяемый метод измерения — это проверка осадки бетонного конуса.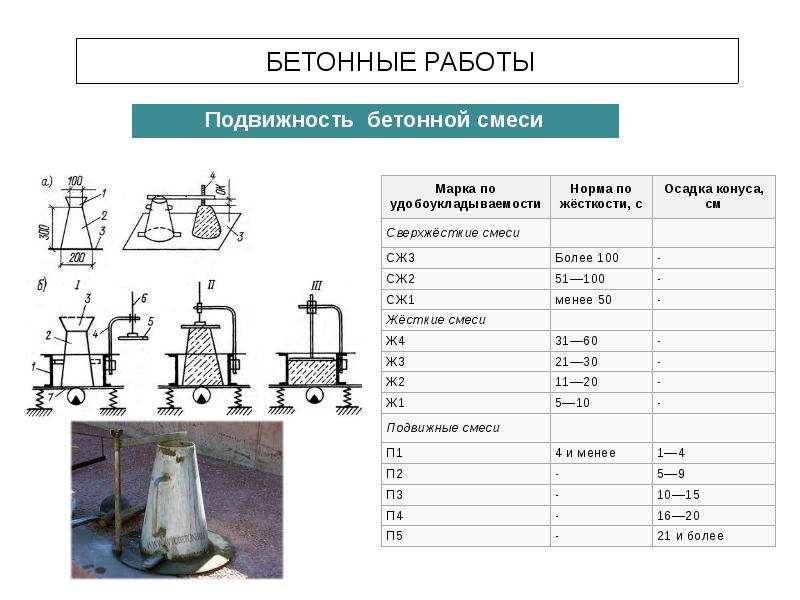
Проверка выполняется в следующей последовательности:
Под действием собственного веса материал оседает, пока не будет достигнуто равновесие между усилиями адгезии и растекания.
С помощью перекрестья линеек измеряется разница между высотой двух конусов, которая определяет подвижность.
При недостаточной текучести бетонщик может прибегнуть к методу разбавления раствора. Отступление от нормативов содержания воды (0,4-0,5 от массы цемента) чревато снижением прочности материала.
Определение эластичности путем анализа монолита
Проверка выполняется следующим образом:
С помощью лабораторного вибростола
При строительстве ответственных конструкций могут проводиться лабораторные измерения текучести смеси. Для этого применяются вибростолы, которые уплотняют свежий бетон.
Подвижность материала может оцениваться двумя методами:
Пористость бетона. Что это такое, и на что она влияет
На вид готовый бетон — сплошная плотная субстанция. На самом деле, в структуре бетона имеются поры.
На самом деле, в структуре бетона имеются поры.
Пористость и плотность обратны по отношению друг к другу: чем выше пористость бетона, тем ниже его прочность.
Как появляются поры в бетоне?
Чтобы понять, откуда в бетоне поры, нужно представлять процесс образования бетонного камня. Составляющие цемента, смешиваясь с водой, вступают в реакции гидратации, в ходе которых образуются новые кристаллические соединения. Но для реакции нужно меньше воды, чем необходимо для замешивания более-менее пластичного раствора, поэтому часть воды не вступает в реакцию. Кроме того, смесь захватывает воздух, который также способствует появлению пор.
Поры в бетоне уменьшают его плотность (и, соответственно, массу кубометра бетона), следовательно, снижают и его прочность.
Применение пластификаторов позволяет более полно вовлечь цемент в реакции гидратации и уменьшить воду затворения, благодаря чему уменьшается пористость бетона: количество пор и их диаметр уменьшается, что повышает плотность и, следовательно, прочность бетона.
Другие факторы, влияющие на плотность бетона
Помимо плотности бетонного камня как такового, на плотность бетона оказывает влияние состав смеси, в том числе, заполнители:
- В самые тяжелые бетоны добавляют стальную стружку. Плотность такого бетона свыше 2500 кг/куб. м
- Плотность тяжелых бетонов от 2100 до 2500 кг/куб. м. В качестве заполнителей используется диабаз, гранит, известняк.
- Облегченный бетон с плотностью 1800—2000 кг/куб. м изготавливают, применяя в качестве заполнителя щебень.
- При изготовлении легких бетонов применяют пористые заполнители — керамзит, туф, вспученный шлак и пемзу.
Классификация и как обозначается
Подвижность бетона обозначается буквой «П». По этому критерию бетонные растворы классифицируются на 5 групп от П-1 до П-5. Чем выше текучесть материала, тем больше цифра, указанная в марке подвижности.
Таблица подвижности смеси из бетона
| Вид смеси | Осадка испытательного конуса, см | Куда заливается | Особенности |
| П-1 | 1-5 | Монолиты с минимальной сложностью конфигурации | Обязательно уплотняется вибрацией |
Жесткие и сверхжесткие смеси, которые имеют нулевую осадку конуса, обозначаются Ж и СЖ (например, СЖ-2).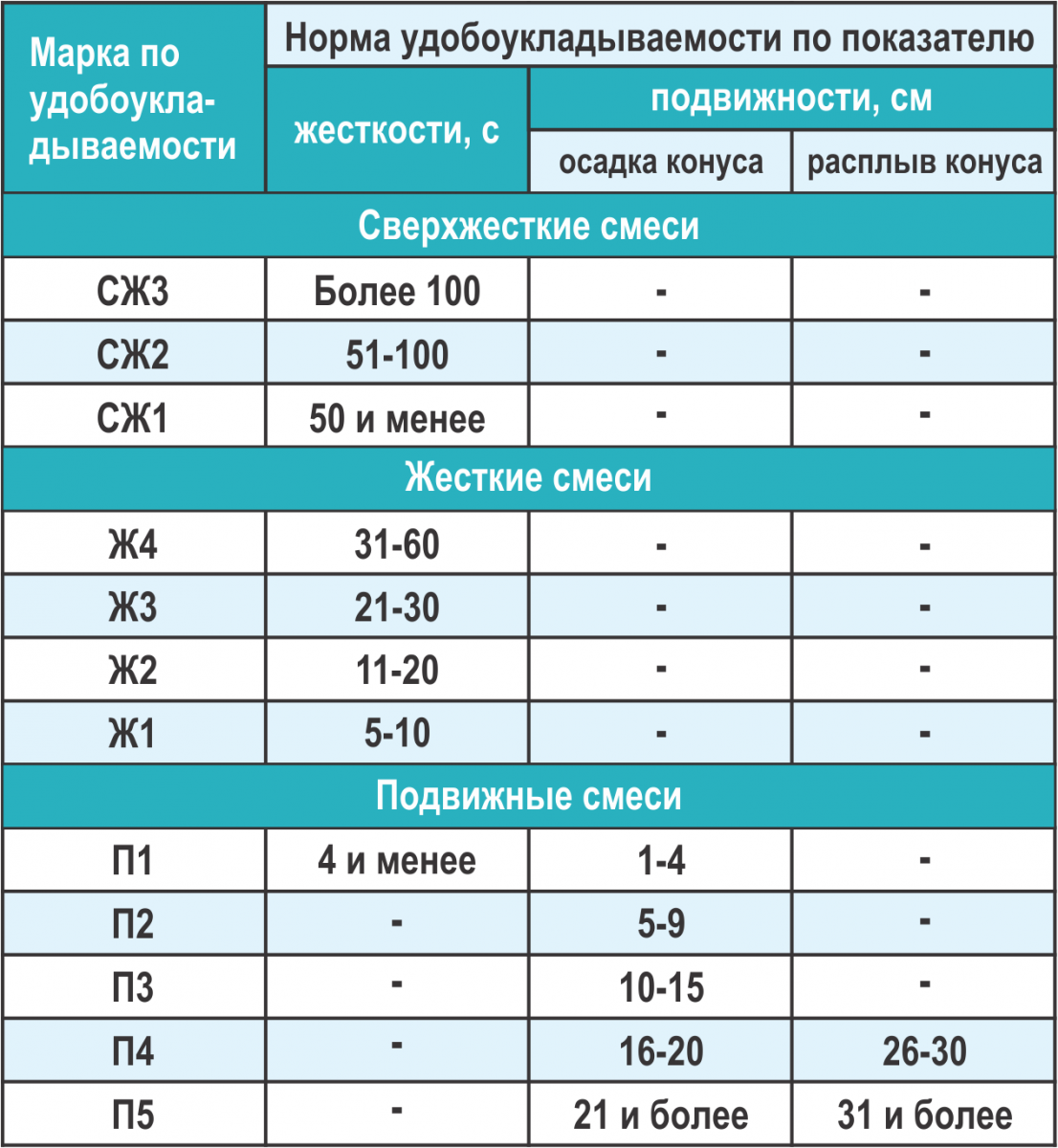 Из-за технологических сложностей укладки в опалубку они применяются в ограниченном диапазоне работ.
Из-за технологических сложностей укладки в опалубку они применяются в ограниченном диапазоне работ.
Температура бетонной смеси
Для набора прочности бетона основополагающее значение имеет температура смеси.
Важно!
Оптимальная температура твердения бетона +18—20°С. Чем ниже температура, тем медленнее происходит набор прочности, и в итоге это влияет на конечные характеристики прочности бетона. При +5°С твердение практически останавливается, а при 0°С и ниже полностью прекращается. Напротив, при высоких температурах +30°С и выше, бетон твердеет слишком быстро. Обе ситуации снижают прочность готовых бетонных конструкций.
Вот почему в условиях неподходящей температуры окружающей среды применяются меры ухода за бетоном: укрывание, прогрев либо, напротив, поливание холодной водой, чтобы обеспечить оптимальные условия набора прочности.
Подвижность бетона. Что такое текучесть бетона
Что представляет собой текучесть бетона
На текучесть бетона влияют следующие параметры:
- марка цемента;
- пропорции цемента и воды;
- плотность бетонного теста;
- размер и форма фракций наполнителя;
- количество и качество компонентов и добавок.

Сохраняемость свойств бетона
Сохраняемостью свойств называют способность бетонной смеси сохранять удобоукладываемость в течение заданного времени.
Применение пластификаторов позволяет замешивать смеси повышенной сохраняемости. По сравнению со смесями, не содержащими специальные добавки, смеси повышенной сохраняемости имеют следующие преимущества:
- переносят длительную транспортировку без потери свойств;
- оптимизируют организацию арматурных, опалубочных и бетонных работ;
- повышают монолитность конструкций благодаря уменьшению количества швов;
- уменьшают потери бетона, связанные с быстрым схватыванием;
- снижают объем работ и затраты электроэнергии;
- повышают качество бетонных конструкций.
Качество бетонных конструкций напрямую зависит от свойств бетонной смеси: подвижности, удобоукладываемости, плотности и пористости, способности смеси сохранять ее свойства, а также от условий, в которых происходит ее отвердевание.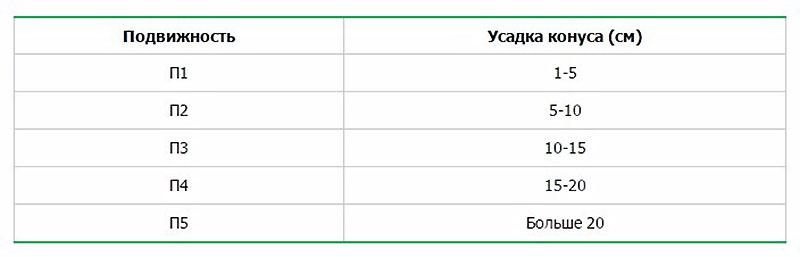 Улучшить все перечисленные показатели смеси позволяет применение специальных добавок для бетона — пластификаторов. Современные пластификаторы — экономичные и удобные в применении жидкости, которые улучшают удобоукладываемость бетона, повышают его плотность и прочность, и позволяют экономить время, расходные материалы, трудозатраты и электроэнергию при производстве бетонных работ.
Улучшить все перечисленные показатели смеси позволяет применение специальных добавок для бетона — пластификаторов. Современные пластификаторы — экономичные и удобные в применении жидкости, которые улучшают удобоукладываемость бетона, повышают его плотность и прочность, и позволяют экономить время, расходные материалы, трудозатраты и электроэнергию при производстве бетонных работ.
Зависимость подвижности от состава смеси
Бетон, применяемый в строительстве, состоит из цемента и нейтральных наполнителей – щебня разных фракций, песка. Его подвижность зависит от соотношения, качества наполнителей и наличия примесей. Чтобы изменить некоторые характеристики применяют специальные присадки, добавки для увеличения текучести называются пластификаторы. Идеальная пластичность достигается при правильном соотношении водоцементной смеси, увеличение количества наполнителей делает ее более жесткой.
Чтобы добиться оптимальной прочности и текучести растворов, пропорция воды и цемента в растворе по массе должна составлять 0,4.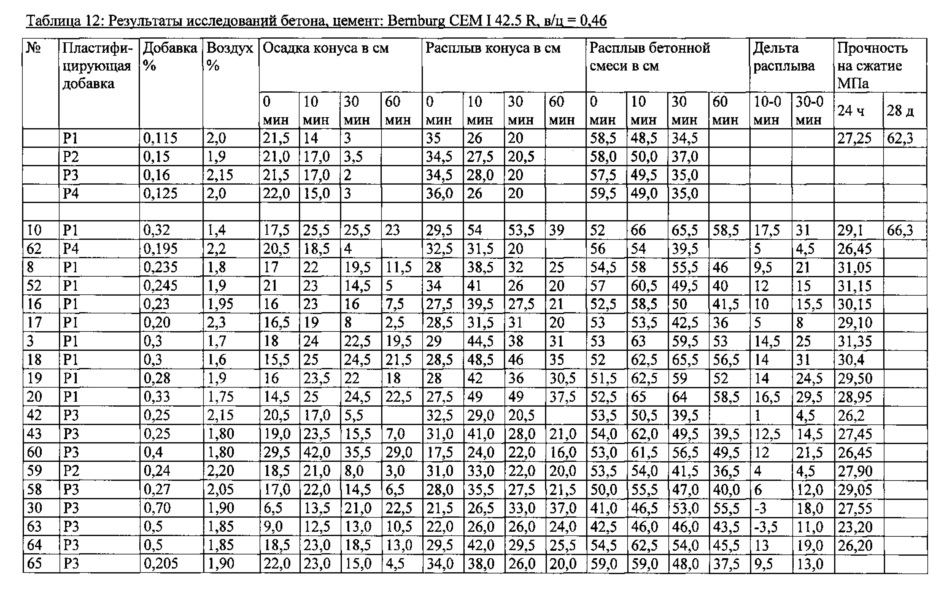 Нарушение этого баланса приводит к снижению прочности после затвердевания. А добавление воды в готовый состав для увеличения подвижности приведет к тому, что расслаиваемость бетонной смеси резко снизит качество конструкции. Малая подвижность достигается добавлением песка, в результате чего она не расслаивается, но для качественной укладки требуется трамбовка.
Нарушение этого баланса приводит к снижению прочности после затвердевания. А добавление воды в готовый состав для увеличения подвижности приведет к тому, что расслаиваемость бетонной смеси резко снизит качество конструкции. Малая подвижность достигается добавлением песка, в результате чего она не расслаивается, но для качественной укладки требуется трамбовка.
График водопотребности бетонной смеси
Повысить подвижность раствора, можно увеличив долю цемента в нем. Это связано с тем, что тонкая фракция цемента обволакивает поверхности зерен наполнителей, не позволяя соприкасаться, трение между ними уменьшается, а текучесть увеличивается. Данный способ повышения текучести не сказывается на прочности, но увеличивается стоимость раствора. Повышает подвижность и укрупнение фракции щебня, поскольку меньшая площадь снижает внутреннее трение. Но галечный щебень не рекомендовано использовать, поскольку его гладкая поверхность снижает прочность состава.
Сильно влияет на показатели П1-П5 наличие различных примесей. Поэтому в щебне или песка неприемлемо большое количество пыли, органических включений или глины. При затвердении такие примеси создают зоны со сниженной прочностью, что сказывается на надежности зданий и сооружений.
Поэтому в щебне или песка неприемлемо большое количество пыли, органических включений или глины. При затвердении такие примеси создают зоны со сниженной прочностью, что сказывается на надежности зданий и сооружений.
После изготовления раствор сохраняет пластичность в течение 2 часов. Чтобы доставить его на место с сохранением нужной текучести применяют пластификаторы. Это присадки, позволяющие сохранять и даже увеличивать пластичность раствора до 25%. Их применение даст возможность отказаться от трамбовки или применения вибрации даже с растворами П2-П3. В их состав входят парафин, эфир фталевой кислоты, фосфаты и другие вещества. Раствор с пластификатором сохраняет показатели текучести на протяжении 6 часов после изготовления, этого достаточно для естественного заполнения пустот. При домашнем строительстве в качестве пластификатора иногда применяют мыло или средства для мытья посуды.
Правильно подобранная пластичность обеспечит быструю и качественную укладку бетона, повысит его технические характеристики после затвердевания. Это достигается оптимальным соотношением компонентов и условиями укладки. Подвижность раствора оперативно подбирается непосредственно во время проведения работ, исходя их этих факторов.
Это достигается оптимальным соотношением компонентов и условиями укладки. Подвижность раствора оперативно подбирается непосредственно во время проведения работ, исходя их этих факторов.
Таблица пластичности
Чтобы упростить эксплуатацию бетонных смесей с разной пластичностью, следует обратить внимание на таблицу, где они систематизированы по этому фактору. Также в таблице находятся и другие свойства удобоукладываемости, включая связность и жесткость.
Согласно информации из таблицы, усадка конуса на 1−1,5 см указывает на принадлежность смеси к группе с повышенной жесткостью, т. е. с малоподвижным составам. Материал с подобными параметрами обозначается маркировкой П1. Марки П2 и П3 обладают усадкой конуса в 5−10 сантиметров и 10−15 см соответственно. Наличие маркировки П4 сообщает о том, что уровень усадки варьируется в пределах 15−20 см. Если показатели еще выше, то бетонный раствор относят к специальной группе П5.
Соответствие конкретной разновидности бетонной смеси одной из вышеперечисленных степеней подвижности регламентируется установленными нормами ГОСТ. Этот государственный стандарт разделяет все растворы на две большие группы:
Этот государственный стандарт разделяет все растворы на две большие группы:
- Сухие смеси (БСС).
- Готовые к употреблению составы (БСГ).
Также существует несколько групп по удобоукладываемости вещества. К первой относятся сверхжесткие модели (СЖ), ко второй — жесткие (Ж), к третьей — подвижные (П).
Расход цемента на 1 куб бетона: таблицы расхода
Первое, что волнует человека, который хочет построить себе дом или любое другое здание или сооружение, это расход строительных материалов. Несмотря на то, что бетон измеряется кубометрами и имеет определенную стоимость, самой дорогой его составляющей всё равно является цемент. Он намного дороже, чем все остальные входящие в его состав компоненты. Именно от цемента зависит стоимость бетона, но чем выше марка смеси, тем больше необходимо потратить цемента. Также существует определенный баланс между маркой и количеством, которое необходимо добавить в бетон. Несведущему человеку производить такие расчёты проблематично, поэтому необходимо изложить информацию очень доступно. Расход цемента на 1 куб бетона строго регламентирован строительными стандартами, а отклонение от этих норм чревато резким снижением качества и непредсказуемыми свойствами после застывания.
Расход цемента на 1 куб бетона строго регламентирован строительными стандартами, а отклонение от этих норм чревато резким снижением качества и непредсказуемыми свойствами после застывания.
Расход цемента на 1 куб бетона
Самое лучшее представление информации подобного рода возможно только в табличном варианте. Пропорции эти сложились десятилетиями. Не стоит идти против строительных стандартов по ГОСТу. Ярким примером могут послужить строительные здания довоенной постройки, которые до сих пор стоят без малейшей трещины.
Таблица пропорций цемента марки М400, песка, щебня для изготовления требуемой марки бетона
Требуемая марка бетона | Пропорции по массе, Ц:П:Щ (килограмм) | Объемный состав на 1 л цемента, П:Щ (литров) | Получаемый объем бетона из 1 литра цемента (литров) |
|---|---|---|---|
М100 | 1 : 4,6 : 7,0 | 4,1 : 6,1 | 7,8 |
М150 | 1 : 3,5 : 5,7 | 3,2 : 5,0 | 6,4 |
М200 | 1 : 2,8 : 4,8 | 2,5 : 4,2 | 5,4 |
М250 | 1 : 2,1 : 3,9 | 1,9 : 3,4 | 4,3 |
М300 | 1 : 1,9 : 3,7 | 1,7 : 3,2 | 4,1 |
М400 | 1 : 1,2 : 2,7 | 1,1 : 2,4 | 3,1 |
М450 | 1 : 1,1 : 2,5 | 1,0 : 2,2 | 2,9 |
Таблица пропорций цемента марки М500, песка, щебня для изготовления требуемой марки бетона
Требуемая марка бетона | Пропорции по массе, Ц:П:Щ (килограмм) | Объемный состав на 1 л цемента, П:Щ (литров) | Получаемый объем бетона из 1 литра цемента (литров) |
|---|---|---|---|
М100 | 1 : 5,8 : 8,1 | 5,3 : 7,1 | 9,0 |
М150 | 1 : 4,5 : 6,6 | 4,0 : 5,8 | 7,3 |
М200 | 1 : 3,5 : 5,6 | 3,2 : 4,9 | 6,2 |
М250 | 1 : 2,6 : 4,5 | 2,4 : 3,9 | 5,0 |
М300 | 1 : 2,4 : 4,3 | 2,2 : 3,7 | 4,7 |
М400 | 1 : 1,6 : 3,2 | 1,4 : 2,8 | 3,6 |
М450 | 1 : 1,4 : 2,9 | 1,2 : 2,5 | 3,2 |
Как видите, чем выше марка цемента, тем меньше его требуется для того, чтобы создать ту или иную марку бетона. Однако следует быть осторожными с высокомарочными цементами из-за крайне быстрого срока застывания. Обычно такие смеси соединяют непосредственно на строительной площадке, а не на бетонном комбинате по той простой причине, что миксер не успеет довезти смесь до места назначения.
Однако следует быть осторожными с высокомарочными цементами из-за крайне быстрого срока застывания. Обычно такие смеси соединяют непосредственно на строительной площадке, а не на бетонном комбинате по той простой причине, что миксер не успеет довезти смесь до места назначения.
Расход цемента на 1м3 бетона в зависимости от марки цемента:
- М-450 – 469 кг;
- М-400 – 417 кг;
- М-300 – 319 кг;
- М-250 – 300 кг;
- М-200 – 241 кг;
- М-150 – 205 кг;
- М-100 – 166 кг.
При изготовлении бетона, как правило, используют марку цемента M-400. Потому как при использовании цемента низкой марки нужно увеличивать количество цемента. Например если взять марку цемента М-300, то по сравнению с цементом марки M-400 его нужно взять больше на 30%.
| Требуемая пластичность бетона | Расход воды при наибольшем размере частиц заполнителей (в л/куб. | |||||||
|---|---|---|---|---|---|---|---|---|
| гравий, мм | щебень, мм | |||||||
| 10 | 20 | 40 | 80 | 10 | 20 | 40 | 80 | |
| Очень пластичный | 215 | 200 | 185 | 170 | 230 | 215 | 200 | 185 |
| Среднепластичный | 205 | 190 | 175 | 160 | 220 | 205 | 190 | 175 |
| Малопластичный | 195 | 180 | 165 | 150 | 210 | 195 | 180 | 165 |
| Непластичный | 185 | 170 | 155 | 140 | 200 | 185 | 170 | 155 |
Оптимальное соотношение песка и щебня при изготовлении 1м3 бетона составляет: песка — 0,5 м3, щебня — 0,8 м3 и часть наполнителя.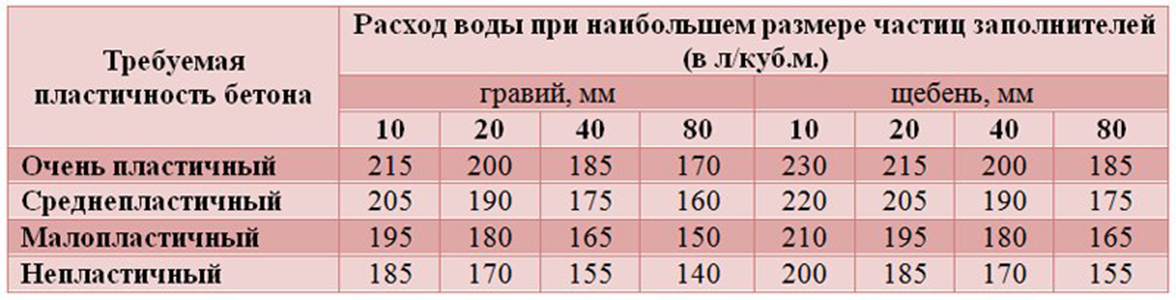 Для бетона марки М200, который используют для фундамента и дорожек, нужно 280 кг цемента, а для бетона марки М300 — 380 кг.
Для бетона марки М200, который используют для фундамента и дорожек, нужно 280 кг цемента, а для бетона марки М300 — 380 кг.
Таблица количества цемента в 1м
3 бетона| Марка бетона | Количество цемента, л | Количество цемента, кг |
| Бетон марки М-100 | 111 | 166 |
| Бетон марки М-150 | 137 | 205 |
| Бетон марки М-200 | 161 | 241 |
| Бетон марки М-250 | 200 | 300 |
| Бетон марки М-300 | 213 | 319 |
| Бетон марки М-400 | 278 | 417 |
| Бетон марки М-450 | 313 | 469 |
Используя данную таблицу, можно с легкостью установить сколько цемента вмещает в себя куб бетона при разных марках и различных задачах, стоящих перед бетоном.
От чего зависит расход цемента
Существует целый ряд факторов, которые существенно влияют на расход цемента:
- Соблюдение пропорций. Только точная мера поможет создать бетон, строго соответствующий марке. Если этого не соблюдать, то лучше не строить здания и сооружения на грани прочностных возможностей, потому что это может быть чревато разломом.
- Расход цемента на 1 куб высокомарочного бетона строго зависит и от марки самого цемента. Обычно пытаются брать только марку 400, потому что более быстрое застывание может создать на строительной площадке неразрушимую глыбу огромных размеров, которую затем придётся бурить и взрывать.
- Адгезивные свойства наполнителей. Всё дело в том, что большое количество острых граней помогает создать устойчивую смесь даже при слабой марке или малом количестве цемента. Этим часто пользуются тогда, когда необходимо создавать ненагруженные конструкции, например, это могут быть декорации в ландшафтном дизайне.
 И это реальный способ существенно сэкономить средства.
И это реальный способ существенно сэкономить средства. - При определенных пропорциях количество цемента влияет исключительно на время застывания, поэтому оно может быть уменьшено примерно на 20%. Опять же, речь идёт о ненагруженных конструкциях.
Перерасход цемента также очень плохо сказывается на качестве бетонной смеси. Граничные значения для каждой марки бетона определены неслучайно, потому что переизбыток может привести к перманентному растрескиванию. Если подойти детально к устройству бетона, то он является так называемой распределенной системой, где каждая его составляющая, начиная от арматуры и заканчивая песчинками, равномерно получает нагрузку. При переизбытке цемента возможно нарушение этого принципа, причём внутренние напряжения будут создаваться даже самим материалом при застывании. Все пропорции выведены на основании сложных инженерных и химических расчётов, поэтому пренебрегать ими нельзя.
Видео: как сделать бетон пропорциями цемента в ведрах
Расход цемента на кирпичную кладку
То, что обычно называют бетоном, у каменщиков называется вяжущим раствором. Всё дело в том, что для этой смеси используют только цемент марки 400. Он позволяет какое-то время работать без риска преждевременного застывания. В растворе его 1 часть против 4 частей песка. Соответственно, на 1 кубометр готовой смеси необходимо потратить 200 литров цемента марки 400. В сухом эквиваленте это 4,5 мешка на 1 кубометр. Количество воды зависит уже от того, каким раствором привык работать каменщик. Поэтому расчёт целесообразно вести на сухую.
Расход раствора на самую распространенную кирпичную кладку в 1,5 кирпича составляет 0,25 кубометра раствора на 1 кубометр кирпича. В количестве это примерно 400 единиц. То есть на 1 кубометр кирпичной кладки в 1,5 кирпича необходимо 1,125 мешка цемента или 56 кг.
Количество, расходуемое на кладку, является усредненным, потому что всё зависит от аккуратности каменщиков. Примерно 3-4% раствора падает вдоль стен, но этого избежать никак нельзя. Также не стоит винить мастеров в этом расходе, потому что кто-то теряет меньше раствора, а кто-то больше. Но, как говорят сами каменщики, большое количество потерь, обычно, получается из-за аккуратности шва. Расход цемента в кирпичной кладке на 1 куб бетона является величиной непостоянной.
Намного более затратной считается кладка в 2 или даже 2,5 кирпича. Там подсчитать количество раствора намного труднее, потому что существует насколько способов сцепки. Также определенное количество могут поглощать пустоты.
Есть ещё один фактор, от которого зависит расход цемента определенной марки на 1 куб бетона. Это точность измерения при составлении смеси. Необходимо пользоваться либо крупными ёмкостями, либо специализированным контрольно-измерительным оборудованием.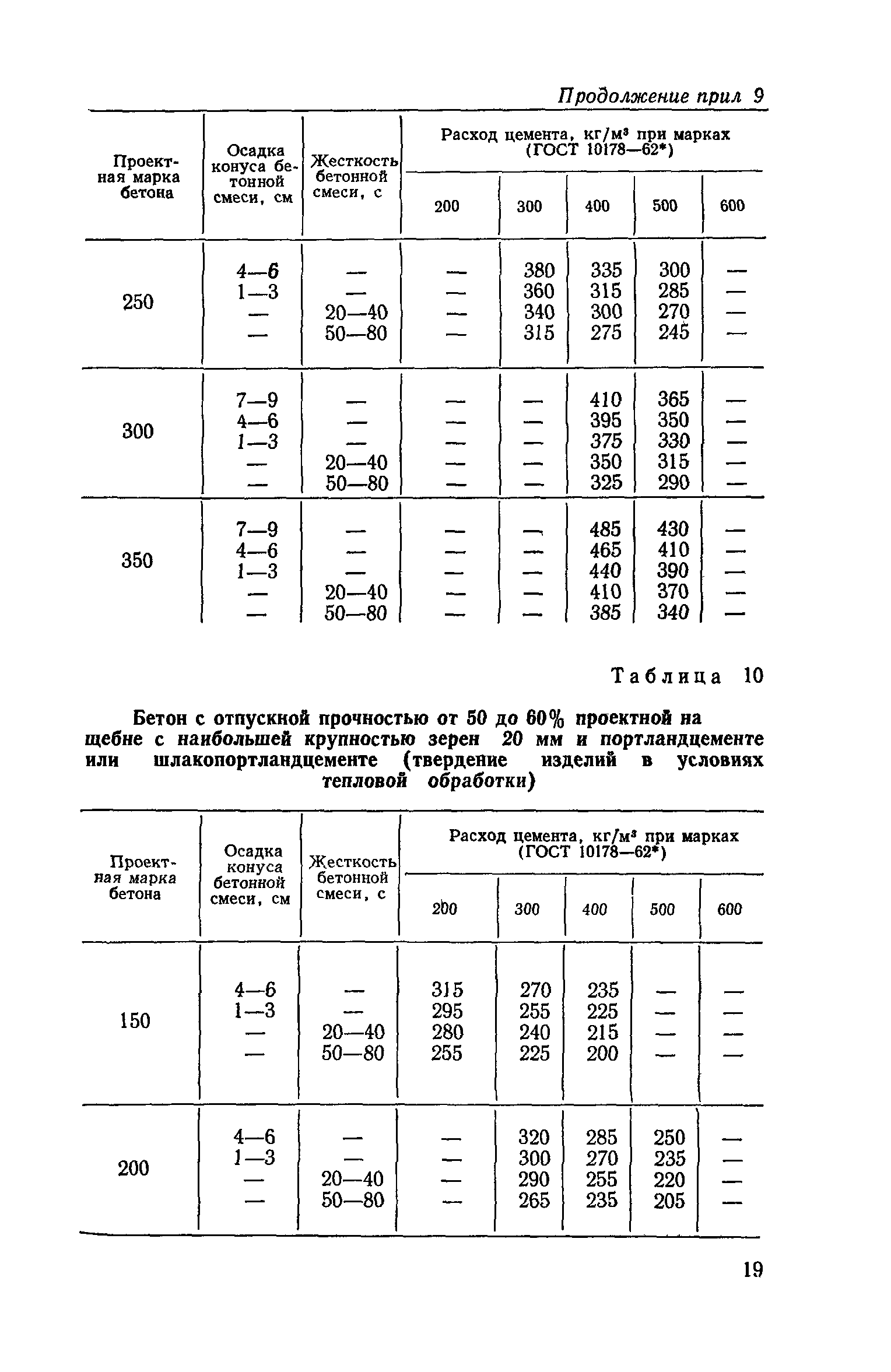 Ведром можно мерить всё что угодно, но только при создании бетона без марки для бытовых нужд, например, для создания дорожки в саду. Во всех остальных случаях точная выдержка пропорций играет величайшую роль, и пренебрегать ею никак нельзя. Расход цемента на 1 куб бетона может сильно варьироваться в случае изготовления смеси «на глаз». Но это плохая практика, потому что свойства бетона после застывания предсказать практически невозможно. Настоятельно рекомендуется соблюдать пропорции, а также выбирать составляющие высшего качества для того, чтобы добиться строгого соответствия стандартам.
Ведром можно мерить всё что угодно, но только при создании бетона без марки для бытовых нужд, например, для создания дорожки в саду. Во всех остальных случаях точная выдержка пропорций играет величайшую роль, и пренебрегать ею никак нельзя. Расход цемента на 1 куб бетона может сильно варьироваться в случае изготовления смеси «на глаз». Но это плохая практика, потому что свойства бетона после застывания предсказать практически невозможно. Настоятельно рекомендуется соблюдать пропорции, а также выбирать составляющие высшего качества для того, чтобы добиться строгого соответствия стандартам.
Видео по теме
Страница не найдена — ZZBO
ВибропрессыWP_Term Object
(
[term_id] => 46
[name] => Вибропрессы УЛЬТРА
[slug] => vibropress-ultra
[term_group] => 0
[term_taxonomy_id] => 46
[taxonomy] => product_cat
[description] =>
[parent] => 45
[count] => 13
[filter] => raw
)
WP_Term Object
(
[term_id] => 149
[name] => Вибропрессы ОПТИМАЛ
[slug] => vibropressy-optimal
[term_group] => 0
[term_taxonomy_id] => 149
[taxonomy] => product_cat
[description] =>
[parent] => 45
[count] => 8
[filter] => raw
)
WP_Term Object
(
[term_id] => 47
[name] => Вибропрессы СТАНДАРТ
[slug] => vibropress-standart
[term_group] => 0
[term_taxonomy_id] => 47
[taxonomy] => product_cat
[description] =>
[parent] => 45
[count] => 8
[filter] => raw
)
WP_Term Object
(
[term_id] => 48
[name] => Вибропрессы МАКСИМАЛ
[slug] => vibropress-maximal
[term_group] => 0
[term_taxonomy_id] => 48
[taxonomy] => product_cat
[description] =>
[parent] => 45
[count] => 9
[filter] => raw
)
WP_Term Object
(
[term_id] => 49
[name] => Передвижные вибропрессы
[slug] => vibropress-mobile
[term_group] => 0
[term_taxonomy_id] => 49
[taxonomy] => product_cat
[description] =>
[parent] => 45
[count] => 2
[filter] => raw
)
WP_Term Object
(
[term_id] => 51
[name] => Вибропрессы блоков ФБС
[slug] => vibropress-fbs
[term_group] => 0
[term_taxonomy_id] => 51
[taxonomy] => product_cat
[description] =>
[parent] => 45
[count] => 4
[filter] => raw
)
WP_Term Object
(
[term_id] => 59
[name] => Вибропрессы для колец ЖБИ
[slug] => zhbi-koltsa
[term_group] => 0
[term_taxonomy_id] => 59
[taxonomy] => product_cat
[description] => Предлагаем оборудование для производства колодезных колец по ГОСТ 8020-90 любых размеров.
Два типа оборудования: вибропрессы КС и виброформы.
[parent] => 0
[count] => 4
[filter] => raw
)
WP_Term Object
(
[term_id] => 52
[name] => Прессы для колки камней
[slug] => vibropress-pk-kolk
[term_group] => 0
[term_taxonomy_id] => 52
[taxonomy] => product_cat
[description] => Прессы для колки камней серии ПК предназначены для раскалывания различного типа камней природного и искусственного происхождения, как по заранее отформованным в них углублениях, так и без последних для получения декоративной (ломанной) лицевой поверхности.
Усилие колки от 10 до 80 тонн. Ширина раскола от 400 мм до 1000 мм.
Идеально подходит для раскалывания гранита, мрамора и других натуральных камней.
[parent] => 45
[count] => 5
[filter] => raw
)
Что такое удобоукладываемость бетонной смеси и как ее измерить?
Область применения бетонных смесей в зависимости от удобоукладываемости
Жесткие бетонные смеси (Ж) – уплотняются (укладываются) при помощи виброплиты, виброрейки катка, бетоноукладчика и т.д. Они применяются для оснований дорог, а так же при возведении фундаментов и других элементов конструкций в качестве бетонной подготовки.
Жесткие бетонные смеси (Ж) бывают следующих марок (жесткость измеряется в секундах):
| Марка | Жесткость, с |
| Ж1 | 5-10 |
| Ж2 | 11-20 |
| Ж3 | 21-30 |
| Ж4 | 31-50 |
| Ж5 | Более 50 |
Подвижная бетонная смесь (П) – представляет из себя литую подвижную однородную массу, которую легче уложить, чем жесткую смесь. Применяется для заливки плит, колонн и др. сооружений с применением бетононасоса. Подвижность бетонной смеси (П) – измеряется в сантиметрах. Чем выше значение, тем больше подвижность. Подвижные бетонные смеси (П) бывают следующих марок:
Применяется для заливки плит, колонн и др. сооружений с применением бетононасоса. Подвижность бетонной смеси (П) – измеряется в сантиметрах. Чем выше значение, тем больше подвижность. Подвижные бетонные смеси (П) бывают следующих марок:
| Марка | Осадка конуса, см |
| П1 | 1-4 |
| П2 | 5-9 |
| П3 | 10-15 |
| П4 | 16-20 |
| П5 | Более 20 |
Факторы, влияющие на подвижность растворов
Технологические особенности бетонной смеси определяет ее состав и свойства применяемых материалов.
Подвижный бетон
В какой степени будут происходить изменения характеристик растворов, и с какими результатами, зависит от следующих факторов:
- Чем выше объем цементного теста, тем более жидкой будет его консистенция, и тем выше подвижность раствора. Добавление в цементное тесто заполнителей уменьшает подвижность в следующей прогрессии — чем больше состав заполнителей и их удельная поверхность, тем меньше подвижность бетона.

- С понижением количества заполнителей и увеличением объема цементного теста, при неизменном В/Ц, подвижность смеси увеличивается, а прочность остается неизменной.
- Значительно влияют на удобоукладываемость растворов свойства цемента. Бетонные растворы, имеющие в своем составе пуццолановый портландцемент, особенно с активной кремнеземистой присадкой, при равном расходе воды, имеют существенно ниже осадку конуса, чем бетоны на обычном портландцементе.
Пуццолановый цемент
- Изменение количества воды — основной фактор при помощи которого регулируется консистенция смеси. С повышением объема воды, при неизменном количестве цемента, подвижность раствора увеличивается, а прочность снижается.
- С увеличением зернистости заполнителей снижается их воздействие на цементный камень, и в результате подвижность бетона увеличивается. Пыль, глинистые компоненты, обычно, понижают удобоукладываемость.
- Немаловажным фактором является соотношение объемов песка и щебня.
 При ненормируемом увеличении этих компонентов друг относительно друга, увеличивается удельная площадь заполнителей и снижается подвижность.
При ненормируемом увеличении этих компонентов друг относительно друга, увеличивается удельная площадь заполнителей и снижается подвижность.
Другими словами, в бетонном растворе существует такая пропорция между заполнителем и цементом, включая соответствие между щебнем и песком, при которой структурная вязкость бетона будет минимальная, подвижность — наибольшая, а для его укладки и уплотнения будет затрачено минимум энергии.
Характеристики бетона по основным показателям
— по прочности: указываются классы прочности на сжатие после твердения: В3,5; В5; В7,5; В10; В12,5; В15; В20; В25; В30; В35; В40; В45; В50; В55; В60; В70; В80; В90; В100. Также применяют бетоны промежуточных классов по прочности на сжатие: В22,5 и В27,5: — по средней плотности: тяжелый бетон марок D2000-D2500, мелкозернистый бетон марок D1800-D2300; — по морозостойкости: марки F50, F75, F100, F150, F200, F300, F400, F500, F600, F800, F1000; — по водонепроницаемости: марки W2, W4, W6, W8, W10, W12, W14, W16, W18, W20.
Марки бетона и их характеристики
ГОСТ 25820-2014 и 26633-2012 определяет марки по средней плотности. Цифра в марке – результат деления массы на объем в кг/м3. Подробнее о марках и классе бетона — в этом видео:
Марки по средней плотности:
- Легкие бетоны: теплоизоляционные – от D200 до D500, конструкционно-теплоизоляционные – от D500 до D2000, конструкционные – не выше D2000
- Мелкозернистые бетоны – от D1800 до D2300
- Тяжелые бетоны – от D2000 до D2500
Марки по истираемости для тяжелых или мелкозернистых бетонов согласно ГОСТ 26633-2012 – G1, G2, G3.
До принятия стандарта СТ СЭВ 1406-78 прочность бетона определялась маркой. После введения в действие указанного норматива прочность стала характеризоваться классом. Маркой по прочности пользуются при выпуске бетона для конструкций, при проектировании которых не учтены требования обеспеченности.
Марки бетона по прочности:
- Легкие теплоизоляционные –от М5 до М25
- Легкие конструкционно-теплоизоляционные– от М35 до М150
- Тяжелые или мелкозернистые: на сжатие – от М50 до М1000, на осевое растяжение – от Pt5 до Pt50, на растяжение при изгибе – от Ptb5 до Ptb100
Цифра в марке указывает предельное неразрушающее усилие в кгс/см2. Соответствие марки по прочности классу приводится в приложении Б к ГОСТ 25820-2000 для легких бетонов, для тяжелых или мелкозернистых – в приложении 1 к ГОСТ 26633-91.
Соответствие марки по прочности классу приводится в приложении Б к ГОСТ 25820-2000 для легких бетонов, для тяжелых или мелкозернистых – в приложении 1 к ГОСТ 26633-91.
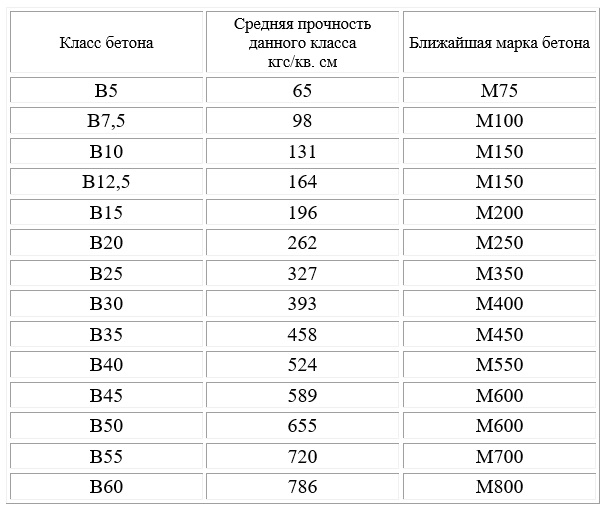
Класс бетона таблица соответствия
Соотношение между классами бетона и марками по прочности на сжатие
| Класс бетона | Марка бетона |
| В7,5 | М100 |
| В10 | М150 |
| В12,5 | М150 |
| В15 | М200 |
| В20 | М250 |
| В22,5 | М300 |
| В25 | М350 |
| В27,5 | М350 |
| В30 | М400 |
| В35 | М450 |
| В40 | М550 |
Примеры условных обозначений
Бетонная смесь тяжелого бетона класса по прочности на сжатие B25, марки по удобоукладываемости П1, марок бетона по морозостойкости F200 и водонепроницаемости W4 будет обозначаться: БСТ В25 П1 F200 W4 ГОСТ 7473-2010
Какой бетон выбрать для ленточного фундамента
Ленточный фундамент часто закладывают при возведении малоэтажных построек. Невысокая нагрузка на основание позволяет заменить плитный фундамент под всей площадью здания проходящей только по периметру лентой. В этой ситуации необходим строгий подход при выборе класса или марки бетона для фундамента дома по прочности.
Невысокая нагрузка на основание позволяет заменить плитный фундамент под всей площадью здания проходящей только по периметру лентой. В этой ситуации необходим строгий подход при выборе класса или марки бетона для фундамента дома по прочности.
Ленточный фундамент собирается из отдельных бетонных блоков или заливается монолитной полосой.Сборка фундамента из блоков практикуется только в России, за рубежом применяют исключительно монолитную конструкцию. Такое положение дел связано с низким технологическим уровнем производства бетонных работ в отечественных условиях и рядом других недостатков.
Согласно ГОСТ 13580-85 на обустройство ленточного фундамента идет тяжелый бетон средней плотности (2200–2500 кг/м3).Требуемый класс по прочности от В10 до В25, конкретное значение зависит от ширины ленты и группы по несущей способности.
На практике допускается использование бетона плотностью 1800–2500 кг/м3. Класс по прочности для подготовки под фундамент В7,5, В10 или В12,5, для самого фундамента – В15, В20, В22,5, В25, в сложных условиях – В30. Чаще всего заказчики покупают бетон класса прочности В15 (соответствует марке М200).
Чаще всего заказчики покупают бетон класса прочности В15 (соответствует марке М200).
Факторы, влияющие на выбор класса товарного бетона:
- Добросовестность производителя и соответствие номинальных характеристик реальным
- Эксплуатационная температура и влажность
- Уровень защиты фундамента от проникновения грунтовых вод и атмосферной влаги
Практически для всех условий подходит бетон БСТ В15 П3 F100 W4 (соответствует марке М200). Если предусматривается эксплуатация при температуре ниже −40 C° cциклическим замораживанием и оттаиванием при постоянном водонасыщении, нужно применять бетон БСТ В20 П3 F150 W4 (соответствует марке М250).
Важно: уверенность в принадлежности бетона к конкретной марке может быть только при самостоятельном изготовлении либо заказе у крупных поставщиков с устоявшейся репутацией. С учетом привычки экономить цемент отечественными производителями рекомендуется приобретать бетон на одну или две марки по прочности выше относительно расчетных параметров.

Определенные поправки при выборе класса прочности вносит характеристика пучинистости грунта.
Выбор класса или марки бетона для фундамента с запасом на экономию цемента поставщиком
| Тип дома | Пучинистость грунта | Класс прочности | Марка прочности |
| Щитовой или каркасный | Слабопучинистый | В15 | М200 |
| Пучинистый | В20 | М250 | |
| Из бруса или бревна | Слабопучинистый | В20 | М250 |
| Пучинистый | В22,5 | М300 | |
| Из газо-, пено- или керамзитобетонных блоков | Слабопучинистый | В22,5 | М300 |
| Пучинистый | В25 | М350 | |
| Из кирпича или монолитного бетона | Слабопучинистый | В25 | М350 |
| Пучинистый | В30 | М400 |
В приведенной эмпирической таблице прочность указана для одноэтажного дома. Для двух- или трехэтажного дома нужно выбирать смесь на марку выше, но не выше М400.
Для двух- или трехэтажного дома нужно выбирать смесь на марку выше, но не выше М400.
Заказ бетонной смеси
Условное обозначение бетонной смеси при заказе должно состоять из сокращенного обозначения бетонной смеси, указанного выше в разделе классификация указывается класс бетона по прочности, марка бетонной смеси по удобоукладываемости. При необходимости добавляются другие нормируемые показатели качества. Например, марка по морозостойкости, марка по водонепроницаемости, средней плотности бетона и др.
Пример заказа бетонной смеси
Бетон М100(Тощий) — соответствует классу бетона В7.5, жесткость бетонной смеси Ж-3, морозостойкости F100, водонепроницаемости W-4. Бетон М100(Тощий) будет обозначаться: В7.5 Ж3F100W4
Что такое удобоукладываемость бетонной смеси и как ее измерить?
Удобоукладываемость — способность бетонной смеси заполнять форму при заданном способе уплотнения и образовывать в результате уплотнения плотную, однородную массу.
В зависимости от показателя удобоукладываемости бетонные смеси подразделяют на группы (классы):
- Жесткие (Ж)
- Подвижные (П)
- Растекающиеся (Р)
Сразу начнем с часто встречающихся – подвижных смесей в простонародье – «жидкий бетон».
Подвижность (П) определяют по осадке конуса.
Осадка конуса (O.K.) — это понятие, характеризующее пластичность бетона. Осадка конуса измеряется в см и чем она больше, тем более подвижен бетон. Как в детстве, дети играют в песочнице и лепят пирожки. Набирают в ведерки или формочки песок, переворачивают и получается «пирожок». Так и в нашем случае, в конус без дна и крышки укладывают бетонную смесь, уплотняют, поднимают конус и смотрят на сколько осела смесь.
Существуют следующие марки по осадке конуса и их значения:
Для практического применения и заказа бетонной смеси важно знать следующее:
- В промышленности обычно при монолитных работах и изготовлении бетонных изделий применяется смесь бетона пластичностью П2-П3 (осадка конуса 5-15см.
 ). Эта смесь требует тщательного вибрирования при укладке и дополнительного физического труда при укладке на большой площади
). Эта смесь требует тщательного вибрирования при укладке и дополнительного физического труда при укладке на большой площади - При укладке бетона в узкие опалубки, колонны, густоармированные конструкции, и прочие труднодоступные для заливки полости используют бетонную смесь с подвижностью П4 (осадка конуса 16-20 см.). Такая смесь, являясь более пластичной, хорошо заполняет форму практически без применения вибратора
- При укладке бетонной смеси с помощью бетононасоса, следует выбирать аналогичную подвижность П4. В последние годы в густоармированных конструкциях все чаще используют литьевые смеси с пластичностью П5 (осадка конуса 21-25 см.), и еще более подвижные (уже характеризующиеся не осадкой конуса, а расплывом)
Данные смеси не могут изготовляться без применения гиперпластифицирующих химических добавок и дополнительных мелких наполнителей (например, кварцевой муки), позволяющих очень легко укладываться смеси и не расслаиваться (то есть щебень внизу, а цементное тесто вверху). Такая смесь очень хорошо заполняет форму опалубки и не требует вибрирования, тем самым сокращая трудозатраты.
Такая смесь очень хорошо заполняет форму опалубки и не требует вибрирования, тем самым сокращая трудозатраты.
Растекающиеся бетонные смеси
Характеризуются маркой по расплыву конуса: Р1, Р2, Р3, Р4, Р5, Р6.
Растекающиеся смеси это в основном самоуплотняющийся бетон (СУБ) – высокоподвижный, нерасслаивающийся бетон, который растекается, заполняя опалубку, и обволакивает арматуру без вибрирования и каких-либо механических усилий. Применяется при высотном строительстве в густоармированных конструкциях и где невозможно уложить бетон вибрированием.
Жесткость бетонной смеси
Марки по жесткости: Ж1, Ж2, Ж3, Ж4 и Ж5.
В основном говоря о жестком, имеют в виду тощий бетон, используемый в основном при дорожном строительстве.
В частном строительстве практически не используется по причине сложности укладки. Его отличие характеризуется пониженным содержанием цемента и воды по отношению к пластичным смесям. Для гидратации цемента (его реакции с водой) иногда воды столь мало, что бетон добирает влагу со временем из грунта.
Его отличие характеризуется пониженным содержанием цемента и воды по отношению к пластичным смесям. Для гидратации цемента (его реакции с водой) иногда воды столь мало, что бетон добирает влагу со временем из грунта.
Для заказа бетона нужной подвижности, обращайтесь к специалистам по телефону или через специальную форму прямо на сайте.
Контроль качества
АО «АБЗ КАПОТНЯ» контролирует качество продукции на всем протяжении процесса, от выбора сырья до готовой бетонной смеси. Производственная лаборатория является самостоятельным структурным подразделением АО «АБЗ КАПОТНЯ», имеет статус службы контроля качества исходного сырья, готовой продукции, а также исследовательских работ в области новых технологий. Производственной лабораторией осуществляется входной, операционный и приёмочный контроль сырьевых материалов и готовой продукции, а также контроль составов бетонных смесей на соответствие ГОСТ, ТУ и другой нормативной документации.
Популярные марки бетона по удобоукладываемости
Характеристикой бетона – «удобоукладываемостью», принято называть способность строительного материала не расслаиваясь легко «заливаться» в опалубку или форму. Межгосударственный стандарт ГОСТ 7473-94 «СМЕСИ БЕТОННЫЕ Технические условия» определяет три условных группы бетонных смесей по удобоукладываемости:
Межгосударственный стандарт ГОСТ 7473-94 «СМЕСИ БЕТОННЫЕ Технические условия» определяет три условных группы бетонных смесей по удобоукладываемости:
- Сверхжесткие;
- Жесткие;
- Подвижные.
Марочная оценка удобоукладываемости конкретной смеси производится на основании следующих характеристик:
- Подвижности и расплыву образца – бетонного конуса. Величину подвижности определяют по осадке тела бетонного образца залитого в специальную металлическую форму-конус. Осадка бетонного конуса, измеренная в сантиметрах после уплотнения штыкования, и есть показатель подвижности бетона;
- Жесткости. Жесткость – это время виброуплотнения образца до требуемой величины.
Все марки бетона по удобоукладываемости обозначаются:
- Подвижные смеси: буквой «П» и цифрой от 1 до 5;
- Жесткие смеси: буквой «Ж» и цифрой от 1 до 4;
- Сверхжесткие смеси: буквой «С» и цифрой от 1 до 3.
Практическое применение марок бетона по удобоукладываемости.
 Таблица
Таблица| Тип бетонной конструкции | Удобоукладываемость, марка |
| Подготовительные работы, бетонные полы, основания автомагистралей и взлетных полос аэродромов | П1 или Ж1 |
| Пол, покрытие автомагистралей и аэродромов, массивные ЖБИ и массивные неармированные или малоармированные конструкции | П1 |
| Армированные плиты перекрытий, балки и другие армированные массивные ЖБИ | П1 или П2 |
| Массивные несущие колонны | П2 |
| Высокоармированные горизонтальные конструкции | П2 или П3 |
| Высокоармированные вертикальные конструкции | П3 или П4 |
| Конструкции заливаемые в скользящую опалубку | П2 или П3 |
| Плиты перекрытий, облицовка тоннелей, фундаменты и другие малорармированные конструкции, заливаемые без уплотнения бетона | П5 или СУ1 |
| Высокоармированные плиты перекрытий, балки, колонны и другие массивные ЖБИ заливаемые без уплотнения бетона | СУ2 или СУ3 |
| Заливка бетона с помощью бетононасосов или пневмонагнетателей | П3, П4 и выше |
Важно знать!
- Жесткие и сверхжесткие бетоны нуждаются в интенсивном вибро-механическом уплотнении: вибрировании и вибротрамбовании.
 В связи с этим изготовление конструкций из жесткого или сверхжесткого бетона возможно исключительно в заводских условиях;
В связи с этим изготовление конструкций из жесткого или сверхжесткого бетона возможно исключительно в заводских условиях; - Увеличение подвижности материала до марки П4-П5 возможно лишь с помощью применения присадок-пластификаторов. Разбавление же бетона без пластификатора водой до подвижности П4-П5 значительно ухудшает его прочностные и другие характеристики.
salecement.ru
Как проверить бетон? | Полезное
Как проверить бетон? А ту ли марку Вам привезли? А тот ли объем? Это самые часто задаваемые вопросы. На самом деле, не будучи специалистом в области строительства очень сложно определить, привезли Вам бетон марки 250 или 150. Дадим лишь некоторые советы. Во-первых, по приезду автобетоносмесителя на объект попросите паспорт на бетонную смесь у водителя и товарно-транспортную накладную. При их отсутствии можете развернуть машину и отправить ее обратно на бетонный завод. Если все имеется, то сравните, что написано в паспорте, а что в ТТН. Марка бетона должна совпадать, как и количество. Производитель должен быть один и в паспорте и в ТТН. Посмотрите на время отгрузки (как правило, на современных заводах на ттн пишется время отгрузки). Во-вторых, чем выше марка бетона, тем больше содержание цемента. Это значит, что бетон средних и высоких марок не должен быть щебенистым. Щебенистым может быть бетон марки 100, 150. Обратите внимание на пластичность бетона! Если бетон очень жидкий, а вы не просили этого при заказе, то, скорее всего бетонную смесь излишне разбавили водой. Это может говорить о недогрузе бетона на заводе. Так же бетонная смесь должна быть однородной! Ни каких расслоений на щебень и цементное молочко быть недолжно. В противном случае это может говорить об излишнем расходе специальных добавок (очень часто их используют для экономии цемента). Такой бетон произведен не по ГОСТам. При заказе бетона всегда спрашивайте, на каких инертных материалах работает завод, на цементе какого производителя, есть ли лаборатория на предприятии.
Производитель должен быть один и в паспорте и в ТТН. Посмотрите на время отгрузки (как правило, на современных заводах на ттн пишется время отгрузки). Во-вторых, чем выше марка бетона, тем больше содержание цемента. Это значит, что бетон средних и высоких марок не должен быть щебенистым. Щебенистым может быть бетон марки 100, 150. Обратите внимание на пластичность бетона! Если бетон очень жидкий, а вы не просили этого при заказе, то, скорее всего бетонную смесь излишне разбавили водой. Это может говорить о недогрузе бетона на заводе. Так же бетонная смесь должна быть однородной! Ни каких расслоений на щебень и цементное молочко быть недолжно. В противном случае это может говорить об излишнем расходе специальных добавок (очень часто их используют для экономии цемента). Такой бетон произведен не по ГОСТам. При заказе бетона всегда спрашивайте, на каких инертных материалах работает завод, на цементе какого производителя, есть ли лаборатория на предприятии.
Компания УралБетонКомплект работает более 8 лет на строительном рынке Екатеринбурга и Свердловской области. Произведенный бетон на нашем заводе проверяется опытными образцами. Лаборатория постоянно следит за инертными материалами. По Вашему желанию, мы можем проверить как уже готовые конструкции, так и бетон, который Вы собираетесь принимать. По всем возникающим вопросам звоните. Мы всегда готовы ответить на все Ваши вопросы. Мы дорожим своей репутацией.
Произведенный бетон на нашем заводе проверяется опытными образцами. Лаборатория постоянно следит за инертными материалами. По Вашему желанию, мы можем проверить как уже готовые конструкции, так и бетон, который Вы собираетесь принимать. По всем возникающим вопросам звоните. Мы всегда готовы ответить на все Ваши вопросы. Мы дорожим своей репутацией.
Определяющая модель пластичности бетона при многоосевом сжатии
https://doi.org/10.1016/j.engstruct.2021.113435Получить права и содержание .Модель описывает поведение бетона при общем многоосевом сжатии.
Особое внимание уделяется бетону при неравномерном пассивном удержании.
Рассмотрены проблемы численной реализации модели.
Точность модели подтверждается сравнением с тестовыми данными.
Abstract
Конструктивные элементы с замкнутым бетоном становятся все более популярными в гражданском строительстве из-за их превосходной прочности и пластичности. В этих конструктивных элементах бетон подвергается вызванным расширением (пассивным) боковым сжимающим напряжениям от ограничивающего устройства (например,г., стальная трубка). Существующие исследования привели к теоретическим моделям, которые точно предсказывают поведение напряжения и деформации бетона при равномерном ограничении (например, бетон в круглых стальных трубах при концентрическом осевом сжатии), но теоретические модели с аналогичной способностью не были созданы для более распространенной ситуации. бетона при неравномерном удержании (например, бетон в прямоугольных стальных трубах). В этой статье представлена трехмерная (3D) определяющая модель пластичности, которая позволяет точно прогнозировать поведение бетона при различных условиях локализации.В предлагаемой модели хорошо зарекомендовавшая себя открытая поверхность прочности с соответствующими открытыми поверхностями текучести сочетается с правилом упрочнения/размягчения, совместимым как с пластическим объемным уплотнением, так и с расширением.
В этих конструктивных элементах бетон подвергается вызванным расширением (пассивным) боковым сжимающим напряжениям от ограничивающего устройства (например,г., стальная трубка). Существующие исследования привели к теоретическим моделям, которые точно предсказывают поведение напряжения и деформации бетона при равномерном ограничении (например, бетон в круглых стальных трубах при концентрическом осевом сжатии), но теоретические модели с аналогичной способностью не были созданы для более распространенной ситуации. бетона при неравномерном удержании (например, бетон в прямоугольных стальных трубах). В этой статье представлена трехмерная (3D) определяющая модель пластичности, которая позволяет точно прогнозировать поведение бетона при различных условиях локализации.В предлагаемой модели хорошо зарекомендовавшая себя открытая поверхность прочности с соответствующими открытыми поверхностями текучести сочетается с правилом упрочнения/размягчения, совместимым как с пластическим объемным уплотнением, так и с расширением. Кроме того, предлагается новая потенциальная поверхность с треугольной девиаторной трассой, калиброванная с использованием имеющихся экспериментальных данных неравномерно ограниченного бетона. Объясняется реализация конститутивной модели в анализе методом конечных элементов с усовершенствованным алгоритмом возврата напряжения, подходящим для новой потенциальной поверхности.В то время как основное внимание в настоящей работе уделяется монотонной нагрузке с преобладанием сжатия, модель может быть объединена с теориями разрушения и повреждения, чтобы изобразить поведение бетона в условиях преобладания растяжения и циклических нагрузок. Производительность предложенной модели оценивается путем сравнения ее предсказаний с широким диапазоном экспериментальных данных, охватывающих однородные активные, однородные пассивные и неоднородные пассивные условия удержания, что демонстрирует возможности и высокую точность предложенной модели.
Кроме того, предлагается новая потенциальная поверхность с треугольной девиаторной трассой, калиброванная с использованием имеющихся экспериментальных данных неравномерно ограниченного бетона. Объясняется реализация конститутивной модели в анализе методом конечных элементов с усовершенствованным алгоритмом возврата напряжения, подходящим для новой потенциальной поверхности.В то время как основное внимание в настоящей работе уделяется монотонной нагрузке с преобладанием сжатия, модель может быть объединена с теориями разрушения и повреждения, чтобы изобразить поведение бетона в условиях преобладания растяжения и циклических нагрузок. Производительность предложенной модели оценивается путем сравнения ее предсказаний с широким диапазоном экспериментальных данных, охватывающих однородные активные, однородные пассивные и неоднородные пассивные условия удержания, что демонстрирует возможности и высокую точность предложенной модели.
Ключевые слова
Ключевые слова
Бетон
Бетон
Замкнутый бетон
Увеличенный бетон
Усложная модель
Конституционная модель
Рекомендуемая статьи Статьи (0)
Просмотреть полный текст © 2021 Опубликовано Fullvier Ltd.
Рекомендуемые статьи
Ссылки
Усовершенствованная модель пластичности при повреждении для прогнозирования циклического поведения простого бетона в условиях многоосного нагружения
Эллингвуд Б. Р. Оценка риска землетрясений строительных конструкций. Инженерия надежности и системная безопасность, 2001, 74(3): 251–262
Google Scholar
Сезен Х. Реагирование на сейсмические воздействия и моделирование железобетонных колонн зданий. Диссертация на докторскую степень. Беркли: Калифорнийский университет, Беркли, 2002 г.
Google Scholar
Элвуд К.Дж.Испытания на вибростенде и аналитические исследования обрушения железобетонных каркасов под действием силы тяжести. Диссертация на докторскую степень. Беркли: Калифорнийский университет, Беркли, 2004 г.
Google Scholar

Zhu L, Elwood KJ, Haukaas T. Классификация и оценка сейсмической безопасности существующих железобетонных колонн. Журнал структурной инженерии, 2007 г., 133 (9): 1316–1330
Google Scholar
Хазелтон С.Б., Гуле С.А., Митрани-Райзер Дж., Бек Дж.Л., Дейрляйн Г.Г., Портер К.А., Стюарт Дж.П., Тачироглу Э. Оценка сейсмических характеристик соответствующего нормам железобетонного здания с моментной рамой. Беркли, Калифорния: Тихоокеанский научно-исследовательский центр землетрясений, 2008 г.
Google Scholar
Явари С. Испытания на вибростенде железобетонных каркасов с несейсмической деталировкой. Диссертация на докторскую степень.Ванкувер: Университет Британской Колумбии, 2011 г.
Google Scholar
Элмер В., Тачироглу Э., МакМайкл Л. Повышение динамической прочности простого бетона за счет пластичности с высокой скоростью деформации с расширением при сдвиге. Международный журнал ударной техники, 2012, 45: 1–15
Международный журнал ударной техники, 2012, 45: 1–15
Google Scholar
Адиби М., Марефат М.С., Аллахвирдизаде Р. Нелинейное моделирование циклической реакции железобетонных соединений балки-колонны, армированных гладкими стержнями.Вестник сейсмостойкого строительства, 2018, 16(11): 5529–5556
Google Scholar
Азади Какаванд М. Р., Аллахвирдизаде Р. Усовершенствованные эмпирические модели для прогнозирования способности осадки менее пластичных железобетонных колонн с изгибными, сдвиговыми или осевыми режимами разрушения. Границы строительства и строительства, 2019, 13(5): 1251–1270
Google Scholar
Фарахманд Х., Азади Какаванд М.Р., Тавуси Тафреши С., Хафиз П.Влияние механических и геометрических параметров на сдвиговые и осевые разрушения колонн в железобетонных каркасах. Ciência e Natura, 2015, 37(6–1): 247–259
Google Scholar

Азади Какаванд М. Р. Предельное состояние материалов. Руководство. Беркли: Калифорнийский университет, Беркли, 2012 г.
Google Scholar
Аллахвирдизаде Р, Ханмохаммади М, Марефат М С.Вероятностное сравнительное исследование введенных сейсмических расчетов и критериев оценки, основанных на характеристиках. Инженерные сооружения, 2017, 151: 206–220
Google Scholar
Аллахвирдизаде Р., Голипур Ю. Оценка надежности прогнозируемых структурных характеристик с использованием нелинейного статического анализа. Вестник сейсмостойкого строительства, 2017, 15(5): 2129–2148
Google Scholar
Кент, округ Колумбия, Парк Р. Изгибные элементы с закрытым бетоном. Журнал структурного отдела, 1971, 97(7): 1969–1990
Google Scholar
Popovics S. Численный подход к полной кривой напряжения-деформации бетона. Исследования цемента и бетона, 1973, 3(5): 583–599
Численный подход к полной кривой напряжения-деформации бетона. Исследования цемента и бетона, 1973, 3(5): 583–599
Google Scholar
Мандер Дж. Б., Пристли М. Дж. Н., Парк Р. Теоретическая модель напряжения-деформации для замкнутого бетона.Журнал структурной инженерии, 1988, 114 (8): 1804–1826
Google Scholar
Скотт Б. Д. Напряженно-деформационное поведение бетона, ограниченного перекрывающимися обручами при низких и высоких коэффициентах деформации. Диссертация на докторскую степень. Лулео: Технологический университет Лулео, 1989
Google Scholar
Чжоу С., Рабчук Т., Чжуан X. Моделирование фазового поля квазистатического и динамического распространения трещин: реализация Comsol и тематические исследования.Достижения в инженерном программном обеспечении, 2018, 122: 31–49
Google Scholar

Чжоу С., Чжуан С., Рабчук Т. Подход к моделированию фазового поля распространения трещин в пороупругих средах. Инженерная геология, 2018, 240: 189–203
Google Scholar
Чжоу С., Чжуан Х., Чжу Х., Рабчук Т. Моделирование фазового поля распространения трещин, ветвления и слияния в горных породах.Теоретическая и прикладная механика разрушения, 2018, 96: 174–192
Google Scholar
Чжоу С., Чжуан С., Рабчук Т. Моделирование фазового поля динамического растрескивания под действием жидкости в пористой среде. Компьютерные методы в прикладной механике и технике, 2019, 350: 169–198
MathSciNet МАТЕМАТИКА Google Scholar
Zhou S, Zhuang X, Rabczuk T. Моделирование фазового поля хрупких трещин сжатия-сдвига в породоподобных материалах: новая движущая сила и гибридная формулировка.Компьютерные методы в прикладной механике и технике, 2019, 355: 729–752
MathSciNet МАТЕМАТИКА Google Scholar
Willam K J. Конструктивная модель трехосного поведения бетона. В: Семинар IABSE по трехосной бетонной конструкции. Цюрих, 1975, 19: 1–30
Google Scholar
Mazars J, Pijaudier-Cabot G. Теория повреждений континуума — Применение к бетону.Журнал инженерной механики, 1989, 115 (2): 345–365
Google Scholar
Pramono E, Willam K. Неявная интеграция составных поверхностей текучести с углами. Инженерные расчеты, 1989, 6(3): 186–197
Google Scholar
Etse G, Willam K. Формулировка энергии разрушения для неупругого поведения простого бетона. Журнал инженерной механики, 1994, 120 (9): 1983–2011
МАТЕМАТИКА Google Scholar
Пивонка П. Конструктивное моделирование трехосно нагруженного бетона с учетом больших сжимающих напряжений: Приложение к испытаниям анкерных болтов на выдергивание. Диссертация на докторскую степень. Вена: Венский технический университет, 2001 г.
Диссертация на докторскую степень. Вена: Венский технический университет, 2001 г.
Google Scholar
Tao X, Phillips DV. Упрощенная модель изотропного повреждения бетона в двухосных напряженных состояниях. Цементно-бетонные композиты, 2005, 27(6): 716–726
Google Scholar
Grassl P, Jirâsek M. Модель пластических повреждений при разрушении бетона. Международный журнал твердых тел и конструкций, 2006 г., 43 (22–23): 7166–7196
МАТЕМАТИКА Google Scholar
Папаниколау В. К., Каппос А. Дж. Конститутивная модель пластичности, чувствительная к ограничению, для бетона при трехосном сжатии. Международный журнал твердых тел и конструкций, 2007 г., 44 (21): 7021–7048
МАТЕМАТИКА Google Scholar
Хогнестад Э. Исследование комбинированного изгиба и осевой нагрузки в железобетонных элементах. Технический отчет. Университет Иллинойса в Урбане Шампейн, 1951 г.
Технический отчет. Университет Иллинойса в Урбане Шампейн, 1951 г.
Google Scholar
Thorenfeldt E. Механические свойства высокопрочного бетона и применение в дизайне. В: Материалы симпозиума, Использование высокопрочного бетона. Норвегия, 1987 г.
Цай В.Т. Одноосное сжатие бетона.Журнал структурной инженерии, 1988, 114 (9): 2133–2136
Google Scholar
Рой Х, Созен М А. Пластичность бетона. Специальные публикации ACI, 1965, 12: 213–235
Google Scholar
Park R, Paulay T. Железобетонные конструкции. John Wiley & Sons, 1975.
Парк Р., Пристли М.Дж.Н., Гилл В.Д. Пластичность квадратных бетонных колонн.Журнал структурного отдела, 1982, 108(4): 929–950
Google Scholar
Шейх С.А., Узумери С. М. Аналитическая модель удержания бетона в связных колоннах. Журнал структурного отдела, 1982, 108(12): 2703–2722
М. Аналитическая модель удержания бетона в связных колоннах. Журнал структурного отдела, 1982, 108(12): 2703–2722
Google Scholar
Йонг Ю. К., Нур М. Г., Нави Э. Г. Поведение поперечно ограниченного высокопрочного бетона при осевых нагрузках. Журнал структурной инженерии, 1988, 114 (2): 332–351
Google Scholar
Эсмаили А., Сяо Ю. Сейсмическое поведение колонн моста, подверженных различным схемам нагрузки. Калифорния: Тихоокеанский исследовательский центр по инженерным исследованиям землетрясений, Калифорнийский университет, 2002 г.
Бичанич Н., Зенкевич О. К. Конструктивная модель бетона при динамической нагрузке. Землетрясение и структурная динамика, 1983, 11 (5): 689–710
Google Scholar
Перзина П. Фундаментальные проблемы вязкопластичности.Успехи прикладной механики, 1966, 9: 243–377
. Google Scholar
Google Scholar
Суарис В., Шах С. П. Конструктивная модель динамического нагружения бетона. Журнал структурной инженерии, 1985, 111 (3): 563–576
Google Scholar
Рабчук Т., Эйбл Дж. Моделирование динамического разрушения бетона бессеточными методами. Международный журнал ударной техники, 2006 г., 32 (11): 1878–1897
Google Scholar
Sima J F, Roca P, Molins C. Циклическая конститутивная модель для бетона. Инженерные сооружения, 2008, 30(3): 695–706
Google Scholar
He W, Wu Y F, Liew K M. Конструктивная модель, основанная на энергии разрушения, для анализа железобетонных конструкций при циклической нагрузке. Компьютерные методы в прикладной механике и технике, 2008, 197(51–52): 4745–4762
МАТЕМАТИКА Google Scholar

Тасними А.А., Лавасани Х.Х. Одноосный определяющий закон для конструкционных бетонных элементов при монотонных и циклических нагрузках. Scientia Iranica, 2011, 18(2): 150–162
Google Scholar
Брекколотти М., Бонфигли М. Ф., Д’Алессандро А., Матерацци А. Л. Конструктивное моделирование простого бетона, подвергаемого циклическому одноосному сжатию. Строительство и строительные материалы, 2015, 94: 172–180
Google Scholar
Мохаррами М., Кутроманос И. Трехосная определяющая модель бетона при циклической нагрузке. Журнал структурной инженерии, 2016, 142(7): 04016039
Google Scholar
Huguet M, Erlicher S, Kotronis P, Voldoire F. Результирующая нелинейная определяющая модель напряжения для железобетонных панелей с трещинами. Инженерная механика разрушения, 2017. С. 176. С. 375–405
. Google Scholar
Google Scholar
Рабчук Т., Беличко Т. Частицы трещин: упрощенный бессеточный метод для произвольно развивающихся трещин. Международный журнал численных методов в технике, 2004 г., 61 (13): 2316–2343
МАТЕМАТИКА Google Scholar
Рабчук Т., Белычко Т. Трехмерный бессеточный метод больших деформаций для произвольно развивающихся трещин. Компьютерные методы в прикладной механике и технике, 2007, 196(29–30): 2777–2799
MathSciNet МАТЕМАТИКА Google Scholar
Рабчук Т., Зи Г., Бордас С., Нгуен-Суан Х. Геометрически нелинейный трехмерный когезионный метод трещин для железобетонных конструкций. Инженерная механика разрушения, 2008, 75(16): 4740–4758
Google Scholar
Рабчук Т., Зи Г., Бордас С., Нгуен-Суан Х. Простой и надежный трехмерный метод крекинг-частиц без обогащения. Компьютерные методы в прикладной механике и технике, 2010, 199(37–40): 2437–2455
Компьютерные методы в прикладной механике и технике, 2010, 199(37–40): 2437–2455
МАТЕМАТИКА Google Scholar
Рабчук Т., Рен Х. Формулировка перидинамики для квазистатического разрушения и контакта в породе. Инженерная геология, 2017, 225: 42–48
Google Scholar
Ren H, Zhuang X, Cai Y, Rabczuk T. Перидинамика двух горизонтов. Международный журнал численных методов в инженерии, 2016 г., 108 (12): 1451–1476
MathSciNet Google Scholar
Баднава Х, Мсех М А, Этемади Э, Рабчук Т. h — адаптивная термомеханическая модель фазового поля разрушения. Конечные элементы в анализе и проектировании, 2018, 138: 31–47
Google Scholar
Zhang Y, Zhuang X. Элементы растрескивания: встроенный подход с самораспространяющимся сильным разрывом для квазихрупкого разрушения.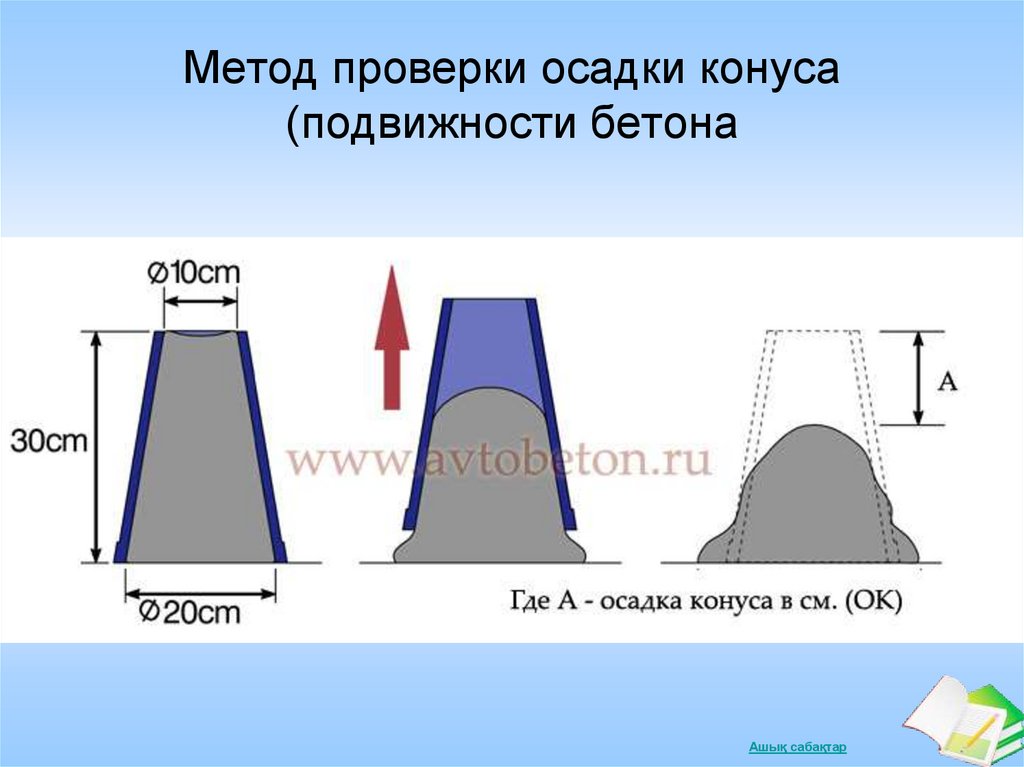 Конечные элементы в анализе и проектировании, 2018, 144: 84–100
Конечные элементы в анализе и проектировании, 2018, 144: 84–100
MathSciNet Google Scholar
Zhang Y, Zhuang X. Метод элементов трещинообразования при динамическом хрупком разрушении. Теоретическая и прикладная механика разрушения, 2019, 102: 1–9
Google Scholar
Чжан Ю., Лакнер Р., Цеймл М., Манг Х. А. Подход с сильным разрывом, встроенным в стандартную формулировку SOS: формулировка элемента, стратегия отслеживания трещин на основе энергии и проверки. Компьютерные методы в прикладной механике и технике, 2015, 287: 335–366
MathSciNet МАТЕМАТИКА Google Scholar
Lee J, Fenves GL. Модель пластического повреждения при циклическом нагружении бетонных конструкций. Журнал инженерной механики, 1998, 124 (8): 892–900
Google Scholar

Grassl P, Xenos D, Nyström U, Rempling R, Gylltoft K. CDPM2: Подход пластичности повреждений к моделированию разрушения бетона. Международный журнал твердых тел и конструкций, 2013, 50(24): 3805–3816
Google Scholar
Зрейд И., Калиске М. Модель микроплоскости бетона с улучшенной пластичностью и повреждением градиента. Журнал вычислительной механики, 2018, 62(5): 1239–1257
MathSciNet МАТЕМАТИКА Google Scholar
Унтереггер Д., Фукс Б., Хофштеттер Г. Модель пластичности повреждений для различных типов неповрежденных горных пород. Международный журнал горной механики и горных наук, 2015 г., 80: 402–411
Google Scholar
Оллер С. Модель непрерывного повреждения фрикционных материалов. Диссертация на докторскую степень. Барселона: Технический университет Каталонии, 1988 г. (на испанском языке)
Google Scholar
Валентини Б. Трехмерная определяющая модель бетона и ее применение для крупномасштабного анализа методом конечных элементов. Диссертация на докторскую степень. Инсбрук: Университет Инсбрука, 2011 г.
Google Scholar
Гопаларатнам В.С., Шах С.П. Реакция мягкого бетона на размягчение при прямом растяжении. Труды журнала ACI, 1985, 82 (3): 310–323
Google Scholar
Карсан И. Д., Йирса Дж. О. Поведение бетона при сжимающих нагрузках. Журнал структурного отдела, 1969, 95: 2543–2563
Google Scholar
Ван Миер Дж. Г. М. Деформационное размягчение бетона в условиях многоосной нагрузки.Диссертация на докторскую степень. Лозанна: Технический университет Эйндховена, 1984 г.
Google Scholar
Taerwe L, Matthys S. Fib Model Code for Concrete Structures 2010. Ernst & Sohn, Wiley, 2013
Ernst & Sohn, Wiley, 2013
Kupfer H, Hilsdorf H K, Rusch H. Поведение бетона при двухосных нагрузках. Труды журнала ACI, 1969, 66 (8): 656–666
Google Scholar
Имран И., Пантазопулу С. Дж. Экспериментальное исследование простого бетона под трехосным напряжением. Журнал материалов ACI, 1996, 93 (6): 589–601
Google Scholar
Reinhardt HW, Cornelissen HAW, Hordijk DA. Испытания на растяжение и анализ разрушения бетона. Журнал структурной инженерии, 1986, 112 (11): 2462–2477
Google Scholar
ABAQUS v6.14 Документация.Dassault Systèmes Simulia Corporation, 2014
Азади Какаванд М. Р., Нойнер М., Шретер М., Хофштеттер Г. Трехмерная континуальная КЭ-модель для прогнозирования нелинейного отклика и режимов отказа RC-рам в анализе начального положения. Вестник сейсмостойкого строительства, 2018, 16(10): 4893–4917
Вестник сейсмостойкого строительства, 2018, 16(10): 4893–4917
Google Scholar
Азади Какаванд М. Р., Тачироглу Э., Хофстеттер Э. Прогнозирование нелинейной реакции и характера повреждений голых и заполненных железобетонных каркасов с использованием трехмерных моделей конечных элементов.В: Материалы 16-й конференции D-A-CH по сейсмостойкому проектированию и динамике конструкций (DA-CH 2019). Инсбрук: Университет Инсбрука, 2019
Google Scholar
Азади Какаванд М. Р., Сезен Х., Тачироглу Э. База данных прямоугольных столбцов. DesignSafe-CI, 2019
Азади Какаванд М. Р., Сезен Х., Тачироглу Э. База данных круговых столбцов. DesignSafe-CI, 2019
%PDF-1.5 % 1731 0 объект эндообъект внешняя ссылка 1731 301 0000000016 00000 н 0000008761 00000 н 0000006316 00000 н 0000008945 00000 н 0000009077 00000 н 0000009114 00000 н 0000009453 00000 н 0000009574 00000 н 0000009600 00000 н 0000009626 00000 н 0000009652 00000 н 0000009860 00000 н 0000010555 00000 н 0000010769 00000 н 0000011387 00000 н 0000012598 00000 н 0000013819 00000 н 0000014626 00000 н 0000015490 00000 н 0000016420 00000 н 0000017336 00000 н 0000018539 00000 н 0000018695 00000 н 0000019099 00000 н 0000019295 00000 н 0000019351 00000 н 0000020337 00000 н 0000021358 00000 н 0000022341 00000 н 0000023054 00000 н 0000069410 00000 н 0000126143 00000 н 0000151118 00000 н 0000151336 00000 н 0000151532 00000 н 0000151606 00000 н 0000151695 00000 н 0000151805 00000 н 0000151987 00000 н 0000152043 00000 н 0000152167 00000 н 0000152261 00000 н 0000152439 00000 н 0000152495 00000 н 0000152592 00000 н 0000152719 00000 н 0000152814 00000 н 0000152870 00000 н 0000153027 00000 н 0000153083 00000 н 0000153173 00000 н 0000153265 00000 н 0000153422 00000 н 0000153478 00000 н 0000153601 00000 н 0000153735 00000 н 0000153888 00000 н 0000153944 00000 н 0000154066 00000 н 0000154203 00000 н 0000154357 00000 н 0000154412 00000 н 0000154540 00000 н 0000154618 00000 н 0000154771 00000 н 0000154826 00000 н 0000154972 00000 н 0000155110 00000 н 0000155256 00000 н 0000155311 00000 н 0000155401 00000 н 0000155497 00000 н 0000155596 00000 н 0000155651 00000 н 0000155751 00000 н 0000155806 00000 н 0000155908 00000 н 0000155963 00000 н 0000156063 00000 н 0000156117 00000 н 0000156212 00000 н 0000156265 00000 н 0000156367 00000 н 0000156420 00000 н 0000156473 00000 н 0000156577 00000 н 0000156632 00000 н 0000156687 00000 н 0000156742 00000 н 0000156830 00000 н 0000156923 00000 н 0000157074 00000 н 0000157129 00000 н 0000157257 00000 н 0000157390 00000 н 0000157445 00000 н 0000157541 00000 н 0000157623 00000 н 0000157678 00000 н 0000157772 00000 н 0000157827 00000 н 0000157925 00000 н 0000157980 00000 н 0000158035 00000 н 0000158090 00000 н 0000158174 00000 н 0000158273 00000 н 0000158328 00000 н 0000158433 00000 н 0000158488 00000 н 0000158543 00000 н 0000158598 00000 н 0000158698 00000 н 0000158753 00000 н 0000158857 00000 н 0000158912 00000 н 0000159022 00000 н 0000159077 00000 н 0000159188 00000 н 0000159243 00000 н 0000159298 00000 н 0000159353 00000 н 0000159443 00000 н 0000159530 00000 н 0000159585 00000 н 0000159693 00000 н 0000159748 00000 н 0000159803 00000 н 0000159858 00000 н 0000160008 00000 н 0000160063 00000 н 0000160160 00000 н 0000160248 00000 н 0000160417 00000 н 0000160472 00000 н 0000160570 00000 н 0000160658 00000 н 0000160713 00000 н 0000160813 00000 н 0000160868 00000 н 0000160970 00000 н 0000161025 00000 н 0000161129 00000 н 0000161184 00000 н 0000161301 00000 н 0000161356 00000 н 0000161472 00000 н 0000161527 00000 н 0000161582 00000 н 0000161637 00000 н 0000161737 00000 н 0000161792 00000 н 0000161893 00000 н 0000161948 00000 н 0000162053 00000 н 0000162108 00000 н 0000162225 00000 н 0000162280 00000 н 0000162396 00000 н 0000162451 00000 н 0000162506 00000 н 0000162561 00000 н 0000162649 00000 н 0000162736 00000 н 0000162791 00000 н 0000162895 00000 н 0000162950 00000 н 0000163060 00000 н 0000163115 00000 н 0000163225 00000 н 0000163280 00000 н 0000163335 00000 н 0000163390 00000 н 0000163509 00000 н 0000163587 00000 н 0000163730 00000 н 0000163786 00000 н 0000163869 00000 н 0000163947 00000 н 0000164002 00000 н 0000164143 00000 н 0000164199 00000 н 0000164283 00000 н 0000164437 00000 н 0000164493 00000 н 0000164591 00000 н 0000164690 00000 н 0000164835 00000 н 0000164891 00000 н 0000164997 00000 н 0000165095 00000 н 0000165232 00000 н 0000165288 00000 н 0000165372 00000 н 0000165515 00000 н 0000165571 00000 н 0000165663 00000 н 0000165755 00000 н 0000165856 00000 н 0000165911 00000 н 0000166020 00000 н 0000166075 00000 н 0000166170 00000 н 0000166225 00000 н 0000166324 00000 н 0000166379 00000 н 0000166434 00000 н 0000166489 00000 н 0000166544 00000 н 0000166600 00000 н 0000166656 00000 н 0000166712 00000 н 0000166768 00000 н 0000166824 00000 н 0000166880 00000 н 0000166935 00000 н 0000167079 00000 н 0000167135 00000 н 0000167219 00000 н 0000167275 00000 н 0000167331 00000 н 0000167421 00000 н 0000167510 00000 н 0000167566 00000 н 0000167622 00000 н 0000167678 00000 н 0000167761 00000 н 0000167839 00000 н 0000167894 00000 н 0000168035 00000 н 0000168090 00000 н 0000168174 00000 н 0000168317 00000 н 0000168372 00000 н 0000168456 00000 н 0000168558 00000 н 0000168613 00000 н 0000168722 00000 н 0000168777 00000 н 0000168872 00000 н 0000168927 00000 н 0000169025 00000 н 0000169080 00000 н 0000169135 00000 н 0000169190 00000 н 0000169245 00000 н 0000169300 00000 н 0000169380 00000 н 0000169461 00000 н 0000169608 00000 н 0000169664 00000 н 0000169745 00000 н 0000169824 00000 н 0000169880 00000 н 0000169982 00000 н 0000170038 00000 н 0000170144 00000 н 0000170200 00000 н 0000170320 00000 н 0000170376 00000 н 0000170480 00000 н 0000170536 00000 н 0000170643 00000 н 0000170699 00000 н 0000170755 00000 н 0000170811 00000 н 0000170867 00000 н 0000170923 00000 н 0000171004 00000 н 0000171083 00000 н 0000171139 00000 н 0000171248 00000 н 0000171304 00000 н 0000171409 00000 н 0000171465 00000 н 0000171576 00000 н 0000171632 00000 н 0000171730 00000 н 0000171786 00000 н 0000171909 00000 н 0000171965 00000 н 0000172055 00000 н 0000172111 00000 н 0000172215 00000 н 0000172271 00000 н 0000172378 00000 н 0000172434 00000 н 0000172490 00000 н 0000172546 00000 н 0000172654 00000 н 0000172710 00000 н 0000172766 00000 н 0000172822 00000 н 0000172963 00000 н 0000173019 00000 н 0000173075 00000 н 0000173131 00000 н 0000173237 00000 н 0000173293 00000 н 0000173349 00000 н 0000173405 00000 н трейлер ]>> startxref 0 %%EOF 1733 0 объект>поток xX{lS?gn\8#1NB`k@BIҖG @x RJBZm]Ƕ>T-RFU!UCۤmZw\;ls;ﻖ &
Предельный анализ и пластичность бетона — 3-е издание
Содержание
ВВЕДЕНИЕ
Теория пластической пластичности
Конституционные уравнения
Экстремума Принципы для жестких пластиковых материалов
Решение задач пластиковых пластиковых
Армированные бетонные конструкции
Условия выхода
Бетон
Условия выхода для армированных дисков
Условия выхода для плит
Укрепление Усилитель
Теория Из простых бетона
Статические условия
Геометрические условия
Виртуальная работа
Конституционные уравнения
Теория плоского напряжения для кулоновских материалов
Применения
Диски
Статические условия
Геометрические условия
Виртуальная работа
Конститутивные уравнения
Точные решения для изотропных дисков
Прочность армированных дисков
Общая теория решений с нижней границей
Модели распорок и связей
Стены сдвига
Однородные армирующие решения
Расчет в соответствии с теорией упругости
Балки
Балки на изгиб 9052 1 Балки при сдвиге
Балки при кручении
Комбинированный изгиб, сдвиг и кручение
Плиты
Статические условия
Геометрические условия
Виртуальная работа, граничные условия
Определяющие уравнения
Точные решения для изотропных плит
Верхние решения Нижние границы для изотропных плит1
Ортотропные плиты
Аналитические оптимальные арматурные решения
Численные методы
мембранное действие
пробивая ножницы плиты
Введение
Внутренние нагрузки или столбцы
Край и угловые нагрузки
Выводящих замечаний
Сдвиг в суставах
Введение
Анализ суставов по теории пластиковых
Различные типы соединений
Прочность соединения арматурных стержней
Введение
Механизм локального разрушения
Механизмы разрушения
Анализ механизмов разрушения
Оценка прочности анкера и соединения
Влияние поперечного давления и опорной реакции
Влияние Tra nsverse Армирование
Заключительные замечания
ПОВРЕЖДЕНИЕ И ПЛАСТИЧНОСТЬ ПОВЕДЕНИЯ БЕТОНА
Европейский конгресс по вычислительным методам в прикладных науках и технике ECCOMAS 2004 P. Нейттаанмяки, Т. Росси, С. Коротов, Э. Ошате, Ж. Перио и Д. Кнёрцер (ред.) Ювяскюля, 24–28 июля 2004 г. УЩЕРБ И < strong>ПЛАСТИЧНОСТЬ ДЛЯ БЕТОНА ПОВЕДЕНИЕ Людовик Джейсон *,o , Жиль Пижодье-Кабо * Антонио Уэрта † и Шахрох Гавамиан o * GeM – Institut de Recherche en Genie Civil et Mécanique Ecole Centrale de Nantes – Université de Nantes – CNRS 1, rue de la Noé – BP – F44300 Nantes, France e-mail: Ludovic.Jason@ec-nantes.fr, Gilles.Pijaudier-Cabot@ec-nantes.fr † Laboratori de Càlcul Numèric Departament de Matemàtica Aplicada III Universitat Politècnica de Catalunya, Jordi Girona 1-3 E-08034 Barcelona, Spain e-mail: Антонио .Huerta@upc.es o EDF Recherche et Développement 1, avenue du Général de Gaulle F
Нейттаанмяки, Т. Росси, С. Коротов, Э. Ошате, Ж. Перио и Д. Кнёрцер (ред.) Ювяскюля, 24–28 июля 2004 г. УЩЕРБ И < strong>ПЛАСТИЧНОСТЬ ДЛЯ БЕТОНА ПОВЕДЕНИЕ Людовик Джейсон *,o , Жиль Пижодье-Кабо * Антонио Уэрта † и Шахрох Гавамиан o * GeM – Institut de Recherche en Genie Civil et Mécanique Ecole Centrale de Nantes – Université de Nantes – CNRS 1, rue de la Noé – BP – F44300 Nantes, France e-mail: Ludovic.Jason@ec-nantes.fr, Gilles.Pijaudier-Cabot@ec-nantes.fr † Laboratori de Càlcul Numèric Departament de Matemàtica Aplicada III Universitat Politècnica de Catalunya, Jordi Girona 1-3 E-08034 Barcelona, Spain e-mail: Антонио .Huerta@upc.es o EDF Recherche et Développement 1, avenue du Général de Gaulle F
Clamart Cedex e-mail: Shahrokh.Ghavamian@edf.fr Ключевые слова: Повреждение, пластичность, модель, бетон Аннотация. Модели упругого повреждения или определяющие законы упругой пластичности не вполне достаточны для описания поведения бетона.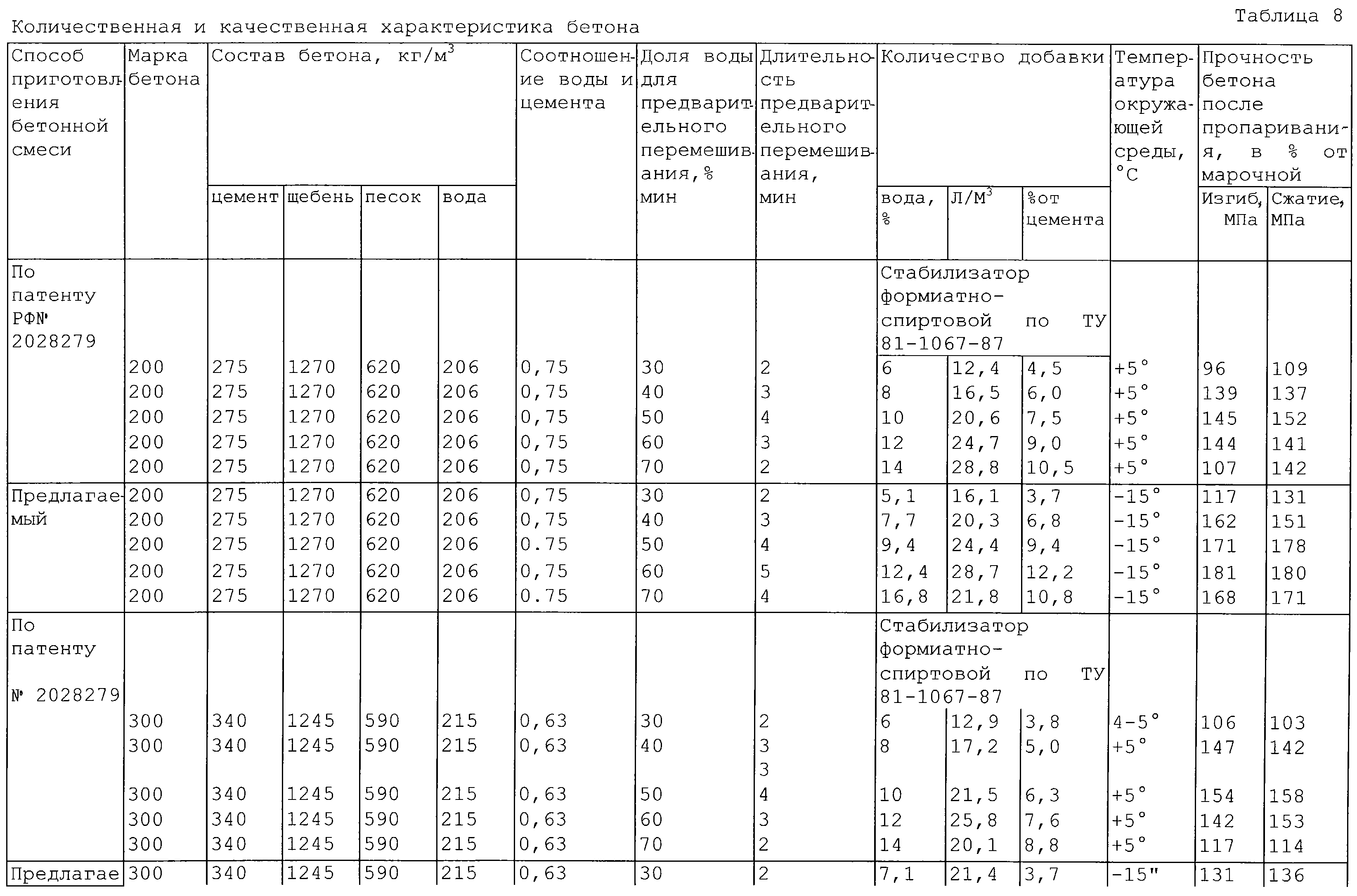 Они действительно не могут воспроизвести наклоны разгрузки при циклических нагрузках, которые экспериментально определяют величину повреждения материала. Таким образом, когда рассматриваются связанные эффекты, особенно в гидромеханических задачах, способность численной модели воспроизводить поведение разгрузки имеет важное значение, поскольку требуется точное значение повреждения. В этом вкладе предлагается комбинированная формулировка «пластмасса-повреждение». Он применяется на простом нагружении растяжением – сжатием для оценки способности закона моделировать элементарные ситуации.Затем рассматриваются два конструкционных применения в виде композитной стальной железобетонной трубы и репрезентативного конструкционного объема здания контейнмента для атомных электростанций. 1
Они действительно не могут воспроизвести наклоны разгрузки при циклических нагрузках, которые экспериментально определяют величину повреждения материала. Таким образом, когда рассматриваются связанные эффекты, особенно в гидромеханических задачах, способность численной модели воспроизводить поведение разгрузки имеет важное значение, поскольку требуется точное значение повреждения. В этом вкладе предлагается комбинированная формулировка «пластмасса-повреждение». Он применяется на простом нагружении растяжением – сжатием для оценки способности закона моделировать элементарные ситуации.Затем рассматриваются два конструкционных применения в виде композитной стальной железобетонной трубы и репрезентативного конструкционного объема здания контейнмента для атомных электростанций. 1
12.9.2 Определение пластичности
Определение классической пластичности металла
Классическая модель пластичности металла позволяет определить предел текучести и неупругое течение металла при относительно низких температурах, когда нагружение относительно монотонно и эффекты ползучести несущественны. Для получения дополнительной информации см. «Классическая пластичность металлов», раздел 22.2.1 Руководства пользователя Abaqus Analysis.
Для получения дополнительной информации см. «Классическая пластичность металлов», раздел 22.2.1 Руководства пользователя Abaqus Analysis.
Использование модели изотропного упрочнения для определения классической пластичности металла
Модель изотропного упрочнения полезна для случаев, связанных с большой пластической деформацией, или для случаев, когда деформация в каждой точке по существу имеет одно и то же направление в пространстве деформаций на протяжении всего анализа.
Для определения модели изотропного упрочнения:
В строке меню диалогового окна Edit Material выберите .
(Информацию об отображении диалогового окна «Редактировать материал » см. в разделе «Создание или редактирование материала», раздел 12.7.1.) Изотропный .
Включите Используйте данные, зависящие от скорости деформации , если вы хотите ввести тестовые данные, показывающие значения предела текучести в зависимости от эквивалентной пластической деформации при различных скоростях эквивалентной пластической деформации.

Столбец Rate появляется в таблице Data .
В качестве альтернативы, если вы хотите определить зависимость скорости деформации с использованием коэффициентов предела текучести, вы должны выбрать из меню. Дополнительные сведения см. в разделе «Определение доходности, зависящей от нормы, с помощью коэффициентов предела текучести». Справочную информацию о зависимости от скорости см. в разделе «Доходность в зависимости от скорости», раздел 22.2.3 Руководства пользователя Abaqus Analysis.
Включить Используйте данные, зависящие от температуры, , чтобы определить данные поведения, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Чтобы определить данные поведения, которые зависят от переменных поля, щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля.
Введите следующие данные в таблицу Data :
Предел текучести
Напряжение, при котором начинается предел текучести.

Скорость
Эквивалентная скорость пластической деформации, для которой применяется кривая напряжения-деформации.
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.При желании используйте меню для ввода дополнительных данных. Подробнее см. в следующих разделах:
Нажмите OK , чтобы создать материал и закрыть диалоговое окно «Редактировать материал».Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (дополнительную информацию см. в разделе «Просмотр и изменение поведения материала», раздел 12.7.2).
Использование линейной кинематической модели циклического упрочнения для определения классической пластичности металла
Использование линейной кинематической модели для определения постоянной скорости циклического упрочнения. См. «Модели для металлов, подвергающихся циклическому нагружению», Раздел 22.2.2 Руководства пользователя Abaqus Analysis для получения дополнительной информации.
См. «Модели для металлов, подвергающихся циклическому нагружению», Раздел 22.2.2 Руководства пользователя Abaqus Analysis для получения дополнительной информации.
Чтобы определить модель линейного кинематического упрочнения:
В строке меню диалогового окна Edit Material выберите .
(Информацию об отображении диалогового окна Edit Material см. в разделе «Создание или редактирование материала», раздел 12.7.1.)
Щелкните стрелку справа от поля Hardening и выберите Кинематика .
Включить Используйте данные, зависящие от температуры, , чтобы определить данные поведения, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Введите следующие данные в таблицу Data :
Предел текучести
Напряжение, при котором начинается предел текучести.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.
Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.При желании используйте меню для ввода дополнительных данных. Подробнее см. в следующих разделах:
Нажмите OK , чтобы создать материал и закрыть диалоговое окно «Редактировать материал». Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (см. «Просмотр и изменение поведения материала», Раздел 12.7.2, для получения дополнительной информации).
Использование модели упрочнения Джонсона-Кука для определения классической пластичности металлов
Модель пластичности Джонсона-Кука особенно подходит для моделирования деформации металлов с высокой скоростью деформации. Эта модель представляет собой особый тип пластичности Мизеса, включающий аналитические формы закона упрочнения и зависимости от скорости. Он обычно используется в динамическом анализе адиабатических переходных процессов. Для получения дополнительной информации см. «Пластичность Джонсона-Кука», раздел 22.2.7 Руководства пользователя Abaqus Analysis.
Для получения дополнительной информации см. «Пластичность Джонсона-Кука», раздел 22.2.7 Руководства пользователя Abaqus Analysis.
Чтобы определить модель упрочнения Джонсона-Кука:
В строке меню диалогового окна Edit Material выберите .
(Информацию об отображении диалогового окна «Редактировать материал » см. в разделе «Создание или редактирование материала», раздел 12.7.1.) Джонсон-Кук .
Введите следующие данные в таблицу Data :
A, B, n и m
Параметры материала, измеренные при температуре перехода или ниже.
Температура плавления
Температура плавления, выше которой материал плавится и ведет себя как жидкость.
Температура перехода
Температура перехода, . Температурная зависимость выражения предела текучести при или ниже температуры перехода отсутствует.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.
Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.При желании используйте меню для ввода дополнительных данных. Подробнее см. в следующих разделах:
Нажмите OK , чтобы создать материал и закрыть диалоговое окно «Редактировать материал». Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (см. «Просмотр и изменение поведения материала», Раздел 12.7.2, для получения дополнительной информации).
Задание пользовательской подпрограммы UHARD для определения классической пластичности металла
Пользовательская подпрограмма UHARD позволяет определить размер поверхности текучести и параметры упрочнения для моделей изотропной пластичности или комбинированного упрочнения.
Чтобы определить классическую пластичность металла с помощью пользовательской подпрограммы UHARD:
В строке меню диалогового окна Edit Material выберите .

(Информацию об отображении диалогового окна Edit Material см. в разделе «Создание или редактирование материала», Раздел 12.7.1.)
Щелкните стрелку справа от поля Усиление и выберите Пользователь .
В таблице Data введите количество Hardening Properties , необходимых в качестве данных в пользовательской подпрограмме UHARD.
Щелкните OK , чтобы создать материал и закрыть диалоговое окно Edit Material . Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (см. «Просмотр и изменение поведения материала», Раздел 12.7.2, для получения дополнительной информации).
Использование модели нелинейного изотропного/кинематического циклического упрочнения для определения классической пластичности металла
Закон эволюции этой модели состоит из двух компонентов: поверхность в пространстве напряжений через подпорку, .
Компонент изотропного упрочнения, который описывает изменение эквивалентного напряжения, определяющего размер поверхности текучести, в зависимости от пластической деформации.
Компонент кинематического упрочнения можно определить, выбрав Комбинированный из списка параметров Упрочнение в диалоговом окне Редактировать материал и введя необходимые данные.
Компонент изотропного упрочнения можно определить, выбрав в меню Циклическое упрочнение и введя данные в появившемся редакторе подопций .
Для получения дополнительной информации о циклическом упрочнении см. «Модели для металлов, подвергающихся циклическому нагружению», раздел 22.2.2 Руководства пользователя Abaqus Analysis.
Чтобы определить модель нелинейного изотропного/кинематического упрочнения:
В строке меню диалогового окна Edit Material выберите .
(Информацию об отображении диалогового окна «Редактировать материал » см.
 в разделе «Создание или редактирование материала», раздел 12.7.1.) Комбинированный .
в разделе «Создание или редактирование материала», раздел 12.7.1.) Комбинированный .Щелкните стрелку справа от поля Тип данных и укажите, как вы хотите определить компонент кинематического упрочнения модели: первый полупериод эксперимента с однонаправленным растяжением или сжатием.
Выберите Параметры , чтобы указать параметры кинематического упрочнения и напрямую.
Выберите Стабилизированный , чтобы предоставить данные напряжения-деформации, полученные из стабилизированного цикла образца, который подвергается симметричным циклам деформации.
Чтобы указать количество обратных напряжений для включения в модель, щелкните стрелки справа от поля Количество обратных напряжений . Количество обратных напряжений по умолчанию равно 1. Максимально допустимое количество обратных напряжений равно 10.
Если вы выбрали Параметры из списка параметров Тип данных , в таблице появятся дополнительные столбцы для указания кинематических параметров упрочнения для нескольких обратных напряжений.
 .
.Включить Используйте данные, зависящие от температуры, , чтобы определить данные поведения, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Чтобы определить данные поведения, которые зависят от переменных поля, щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля.
Если вы выбрали Стабилизированный из списка опций Тип данных , вы можете включить Использовать данные, зависящие от диапазона деформации .Эта опция полезна, если формы кривых напряжения-деформации значительно различаются для разных диапазонов деформации.
В таблицу Данные введите данные, относящиеся к вашему выбору Тип данных (не все из следующих параметров будут применяться):
Предел текучести
Напряжение, при котором начинается предел текучести.

Предел текучести при нулевой пластической деформации
Предел текучести при нулевой пластической деформации, .
Параметр кинематической жесткости C1
Параметр кинематической жесткости, .
Гамма 1
Параметр кинематического упрочнения, .
Параметры кинематического упрочнения C k и гамма k
Параметры кинематического упрочнения и для нескольких обратных напряжений.
Поле n
Предопределенные переменные поля.
Диапазон деформации
Диапазон деформации, при котором получается кривая напряжения-деформации.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.Чтобы определить компонент изотропного упрочнения модели, выберите в меню Циклическое упрочнение и введите необходимые данные в появившемся редакторе подопций .
 Дополнительные сведения см. в разделе «Определение компонента изотропного упрочнения нелинейной модели изотропного/кинематического упрочнения».
Дополнительные сведения см. в разделе «Определение компонента изотропного упрочнения нелинейной модели изотропного/кинематического упрочнения».При желании используйте другие опции меню для ввода дополнительных данных. Подробнее см. в следующих разделах:
Нажмите OK , чтобы создать материал и закрыть диалоговое окно «Редактировать материал». Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (дополнительную информацию см. в разделе «Просмотр и изменение поведения материала», раздел 12.7.2).
Определение компонента изотропного упрочнения нелинейной модели изотропного/кинематического упрочнения
Редактор подопций позволяет определить эволюцию области упругости для модели нелинейного изотропного/кинематического упрочнения.Для получения дополнительной информации см. следующие разделы:
Для определения компонента изотропного упрочнения:
Создайте модель материала, как описано в разделе «Использование нелинейной модели изотропного/кинематического циклического упрочнения для определения классической пластичности металла».

В меню диалогового окна Edit Material выберите .
Появится редактор подопций .
Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Чтобы определить данные, которые зависят от переменных поля, щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля.
Укажите, как вы хотите определить компонент изотропного упрочнения:
Включить Используйте параметры , если вы хотите ввести параметры материала экспоненциального закона.
Выключить Используйте параметры , если вы хотите определить изменение размера поверхности текучести как функцию эквивалентной пластической деформации в табличной форме.
Если вы включили Используйте параметры , введите следующие данные в таблицу Данные :
Эквивалентное напряжение
Эквивалентное напряжение, определяющее диапазон упругой деформации при нулевом размере пластической деформации.

Q-бесконечность
Параметр изотропного упрочнения, .
Параметр упрочнения b
Параметр изотропного упрочнения, b .
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.Если вы отключили Используйте параметры , введите следующие данные в таблицу Данные :
Эквивалентное напряжение
Эквивалентное напряжение, определяющее размер диапазона упругости.
Эквивалентная пластическая деформация
Эквивалентная пластическая деформация.
Поле n
Предопределенные переменные поля.
Вам может потребоваться развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см.
 в разделе «Ввод табличных данных», раздел 3.2.7.
в разделе «Ввод табличных данных», раздел 3.2.7.Щелкните OK , чтобы вернуться в диалоговое окно Edit Material .
Определение предела текучести в зависимости от предела текучести с коэффициентами предела текучести
Abaqus позволяет точно определить поведение текучести материала, когда предел текучести зависит от скорости деформации, а ожидаемая скорость деформации значительна.Зависимость от скорости деформации можно задать двумя способами:
. Введите кривые упрочнения при различных скоростях деформации напрямую, как описано в следующих разделах:
. Определите коэффициенты предела текучести, чтобы указать зависимость от скорости независимо, как описано в процедуре. ниже.
Чтобы определить предел текучести с использованием коэффициентов напряжения:
Создайте модель материала, как описано в одном из следующих разделов:
В меню диалогового окна Edit Material выберите Rate Зависимый .

Появится редактор подопций .
Щелкните стрелку справа от поля Упрочнение и выберите метод определения зависимостей упрочнения:
Выберите Степенной закон , чтобы определить коэффициенты предела текучести с помощью закона перенапряжения Купера-Саймондса.
Выберите Табличный , чтобы ввести коэффициенты предела текучести непосредственно в табличной форме в зависимости от эквивалентных скоростей пластической деформации.
Выберите Johnson-Cook , чтобы использовать аналитическую форму Johnson-Cook для определения R .
Если применимо, включите Использовать данные, зависящие от температуры , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Если применимо, щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.

Если вы выбрали Power Law из списка параметров Hardening , введите следующие данные в таблицу Data :
Field n
9
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.Если вы выбрали Коэффициент текучести из списка параметров Закалка , введите следующие данные в таблицу Данные :
Эквивалентная скорость пластической деформации
Эквивалентная скорость пластической деформации (или абсолютное значение скорости осевой пластической деформации при одноосном сжатии для модели разрушаемой пены).
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.
в разделе «Ввод табличных данных», раздел 3.2.7.Если вы выбрали Johnson-Cook из списка опций Hardening , введите следующие данные в таблицу Data : и полевые переменные.
Нулевая точка эпсилон
Постоянная материала, не зависящая от переменных температуры и поля.
Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.
Щелкните OK , чтобы вернуться в диалоговое окно Edit Material .
Определение анизотропной текучести и ползучести
Abaqus предлагает модель анизотропной текучести и ползучести для материалов, демонстрирующих различное поведение текучести или ползучести в разных направлениях.Вы можете определить анизотропную текучесть или ползучесть, задав отношения напряжений, которые применяются в потенциальной функции Хилла. Для получения дополнительной информации см. раздел «Анизотропная текучесть/ползучесть», раздел 22.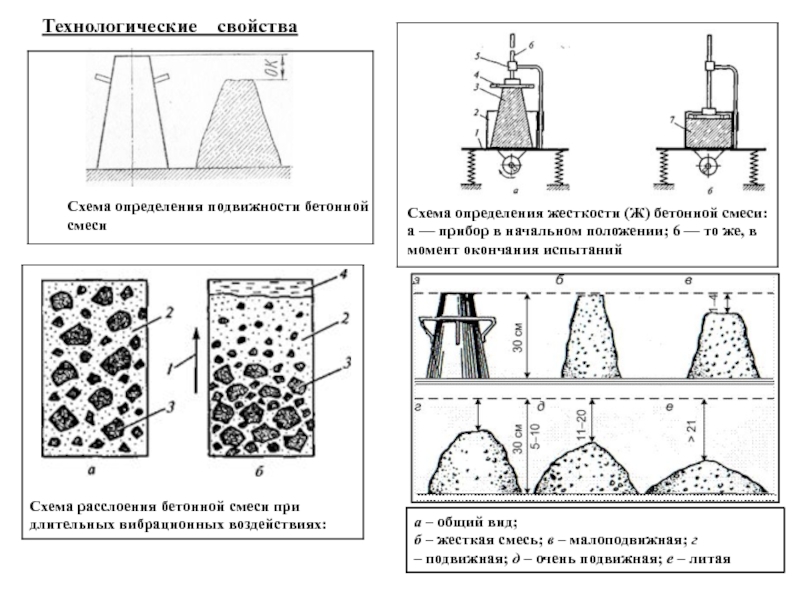 2.6 Руководства пользователя Abaqus Analysis.
2.6 Руководства пользователя Abaqus Analysis.
Для определения анизотропной текучести или ползучести:
Создайте модель материала, как описано в одном из следующих разделов.
Появится редактор подопций .
Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Введите следующие данные в таблицу Data :
R11, R22, R33, R12, R13 и R23
Коэффициент текучести или напряжения ползучести.
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.
Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.Щелкните OK , чтобы вернуться в диалоговое окно «Редактировать материал «.
Использование определяющей модели Oak Ridge National Laboratory (ORNL) в расчетах пластичности и ползучести (1981).Конститутивная теория не связана с не зависящей от скорости реакцией пластичности и зависящей от скорости реакцией ползучести, каждая из которых подчиняется отдельному конститутивному закону. Для получения дополнительной информации см. раздел «ORNL — Конститутивная модель Окриджской национальной лаборатории», раздел 22.2.12 Руководства пользователя Abaqus Analysis, и «Конститутивную теорию ORNL», раздел 4.3.8 Руководства по теории Abaqus.
Чтобы задать определяющую модель, разработанную Окриджской национальной лабораторией:
Создайте модель материала, как описано в одном из следующих разделов: или .

Появится редактор подопций .
В поле Коэффициенты насыщения для кинематического сдвига введите значение параметра A, равного коэффициентам насыщения для кинематического сдвига, вызванного деформацией ползучести. Этот параметр определяется уравнением (15) раздела 4.3.3-3 ядерного стандарта. Значение по умолчанию – 0,3. Установите A=0.0, чтобы использовать версию Стандарта 1986 года.
В поле Скорость кинематического смещения относительно деформации ползучести введите значение параметра H, равного скорости кинематического смещения относительно деформации ползучести.Этот параметр определяется уравнением (7) раздела 4.3.2–1 ядерного стандарта. Установите H=0.0, чтобы использовать версию Стандарта 1986 года. Если этот параметр опущен, Abaqus определяет значение H в соответствии с разделами 4.3.3–3 редакции Стандарта 1981 года.
При желании включите Вызов процедуры сброса , чтобы вызвать дополнительную процедуру сброса, описанную в разделе 4.
 3.5 стандарта для ядерной энергетики.
3.5 стандарта для ядерной энергетики.Щелкните OK , чтобы вернуться в диалоговое окно Edit Material .
Определение температуры отжига упругопластического материала
Когда температура точки материала превышает температуру отжига, Abaqus предполагает, что точка материала теряет память закалки. Вы можете указать температуру отжига и, при желании, определить ее в терминах полевых переменных. Дополнительную информацию см. в разделе «Отжиг или плавление», раздел 22.2.5 Руководства пользователя Abaqus Analysis.
Чтобы задать температуру отжига:
Создайте модель материала, как описано в одном из следующих разделов.
Появится редактор подопций .
Щелкайте по стрелкам справа от поля Число переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависит температура отжига.
Введите в таблицу Data следующие данные:
Температура отжига
Значение температуры отжига, .

Поле n
Предопределенные переменные поля.
Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.Щелкните OK , чтобы вернуться в диалоговое окно «Редактировать материал «.
Определение пластичности крышки
Abaqus позволяет определять параметры поверхности текучести для упругопластических материалов, использующих модифицированную модель пластичности Друкера-Прагера\Кэпа. Дополнительную информацию см. в разделе «Модифицированная модель Друкера-Прагера/Кэпа», раздел 22.3.2 Руководства пользователя Abaqus Analysis.
Задание поведения пластичности покрышки
Модифицированную модель пластичности Друкера-Прагера/Кэпа можно использовать для моделирования геологических материалов, текучесть которых зависит от давления. Добавление поверхности текучести колпачка помогает контролировать дилатацию объема, когда материал поддается сдвигу, и обеспечивает механизм неупругого отверждения для представления пластического уплотнения.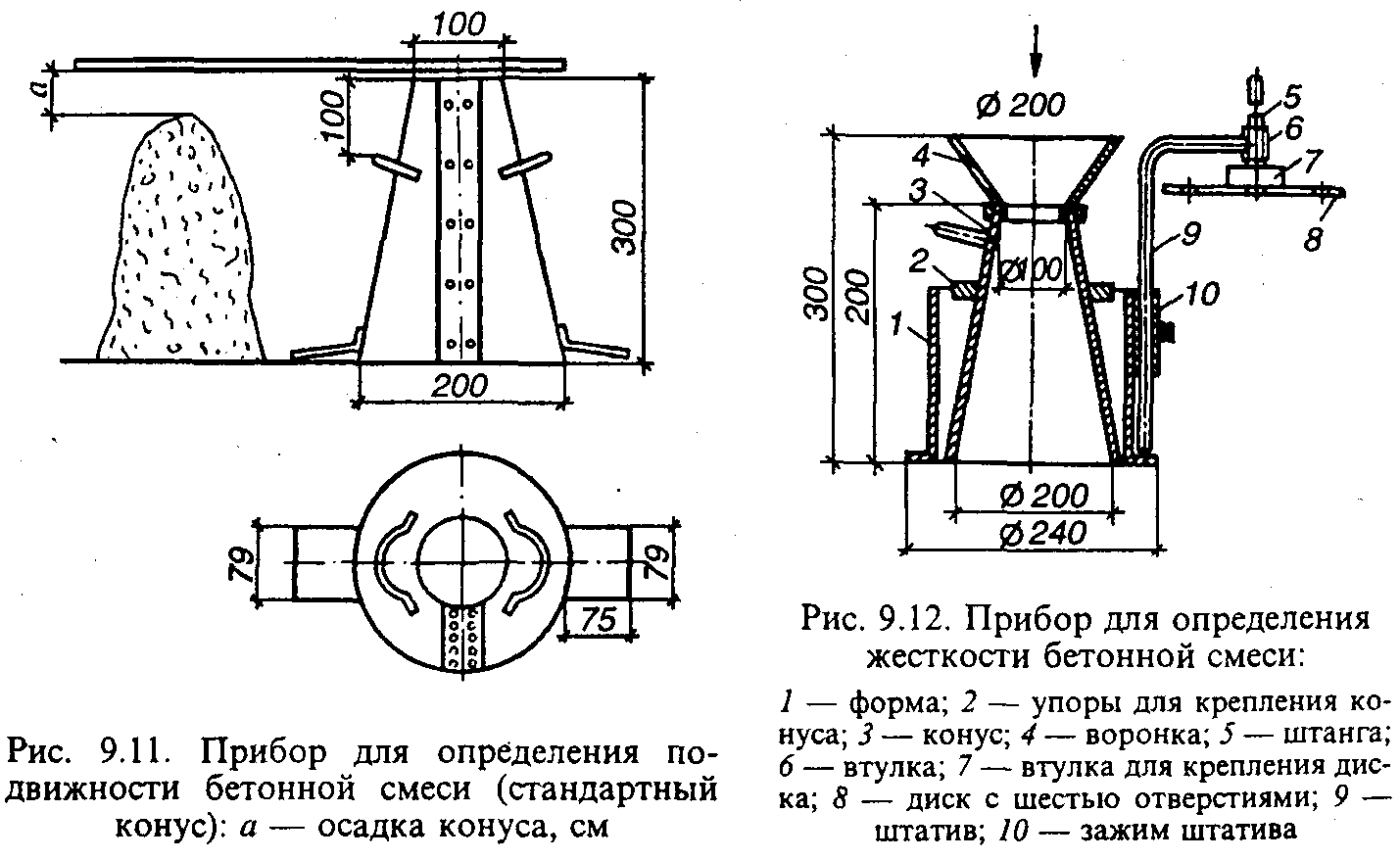 Вы также можете определить неупругое зависящее от времени поведение (ползучесть) в сочетании с пластическим поведением в анализе Abaqus/Standard.
Вы также можете определить неупругое зависящее от времени поведение (ползучесть) в сочетании с пластическим поведением в анализе Abaqus/Standard.
Для получения дополнительной информации о пластичности крышки см. «Модифицированная модель Друкера-Прагера/Кэпа», раздел 22.3.2 Руководства пользователя Abaqus Analysis.
Для определения пластичности крышки:
В строке меню диалогового окна Edit Material выберите .
(Информацию об отображении диалогового окна «Редактировать материал» см. в разделе «Создание или редактирование материала», раздел 12.7.1.)
Включить Использовать данные, зависящие от температуры .
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
в таблице данных .
 p – q самолет (Abaqus/Explicit).(Единицы ФЗ 2 .)
p – q самолет (Abaqus/Explicit).(Единицы ФЗ 2 .)Угол трения
Угол трения материала, , в плоскости p – t (Abaqus/Standard) или в плоскости q 8 p (Абакус/Эксплицит). Введите значение в градусах.
Эксцентриситет крышки
Параметр эксцентриситета крышки, R . Его значение должно быть больше нуля (обычно ).
Init Yld Surf Pos
Исходное положение поверхности текучести крышки, .
Переход Surf Rad
Параметр радиуса поверхности перехода, . Его значение должно быть небольшим числом по сравнению с единицей. Если вы оставите это поле пустым, значение по умолчанию равно 0,0 (т. е. поверхность перехода отсутствует). Если вы включаете свойства ползучести в модель материала, вы должны установить их равными нулю.
Отношение напряжения течения
Отношение напряжения течения при трехосном растяжении к напряжению течения при трехосном сжатии, K .
 Значение K должно быть таким, чтобы .Если оставить это поле пустым или ввести значение 0,0, Abaqus по умолчанию использует значение 1,0. Если вы включаете свойства ползучести в модель материала, вы должны установить K равным 1,0. Этот параметр применяется только к анализам Abaqus/Standard.
Значение K должно быть таким, чтобы .Если оставить это поле пустым или ввести значение 0,0, Abaqus по умолчанию использует значение 1,0. Если вы включаете свойства ползучести в модель материала, вы должны установить K равным 1,0. Этот параметр применяется только к анализам Abaqus/Standard.Поле n
Предопределенные переменные поля.
Для определения упрочняющей части модели пластичности крышки выберите в меню. Подробные инструкции см. в разделе «Определение параметров упрочнения для модели пластичности колпачка».
Если вы хотите указать поведение ползучести крышки, выберите один из следующих вариантов в меню:
Выберите, чтобы выбрать механизм когезионной ползучести, который соответствует типу пластичности, активной в пластичности разрушения при сдвиге.
Выберите, чтобы выбрать механизм консолидации, соответствующий типу пластичности, активной в области пластичности шапки.

Щелкните OK , чтобы создать материал и закрыть диалоговое окно Edit Material . Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (дополнительную информацию см. в разделе «Просмотр и изменение поведения материала», раздел 12.7.2).
Определение параметров упрочнения для модели пластичности крышки при желании функция температуры и других предопределенных полевых переменных. Диапазон значений, для которого вы определяете, должен быть достаточным для включения всех значений эффективного напряжения давления, которому будет подвергаться материал во время анализа.
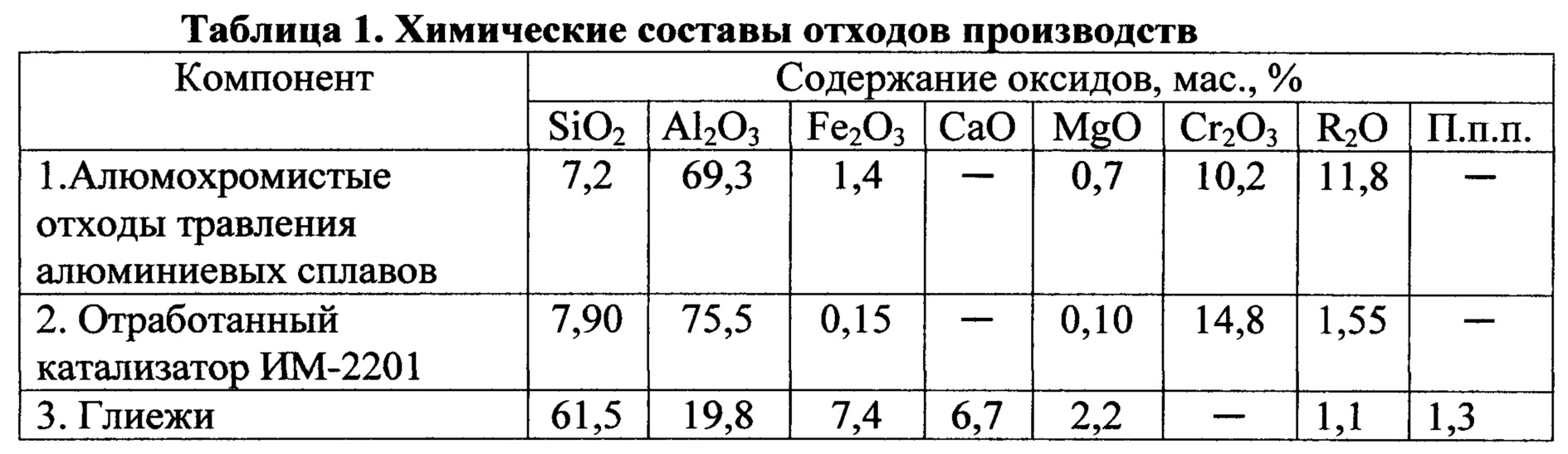
Дополнительную информацию см. в разделе «Модифицированная модель Друкера-Прагера/Кэпа», раздел 22.3.2 Руководства пользователя Abaqus Analysis.
Для определения упрочнения крышки:
Создайте модель материала, как описано в разделе «Задание поведения пластичности крышки».
В меню диалогового окна Edit Material выберите Cap Hardening .
Появится редактор подопций .
Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
В таблицу Данные введите следующие данные:
Предел текучести
Предел текучести при гидростатическом давлении.
 (Исходное табличное значение должно быть больше нуля, и значения должны увеличиваться с увеличением объемной неупругой деформации.)
(Исходное табличное значение должно быть больше нуля, и значения должны увеличиваться с увеличением объемной неупругой деформации.)Vol Plas Strain
Абсолютное значение соответствующей объемной неупругой деформации.
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.Щелкните OK , чтобы вернуться в диалоговое окно «Редактировать материал «.
Определение параметров ползучести для модели пластичности шапки
Модель ползучести шапки имеет два возможных механизма, которые активны в разных областях нагружения: один представляет собой механизм сцепления, который соответствует типу пластичности, действующей при сдвиге-разрушении. области пластичности, а другой представляет собой механизм консолидации, который соответствует типу пластичности, действующей в области пластичности шапки.
Для получения дополнительной информации см. «Формула ползучести» в «Модифицированная модель Друкера-Прагера/Кэпа», Раздел 22.3.2 Руководства пользователя Abaqus Analysis.
Для определения ползучести колпачка:
Создайте модель материала, как описано в разделе «Задание поведения пластичности колпачка».
В меню диалогового окна Edit Material выберите либо Cap Creep Cohesion , либо Cap Creep Consolidation . (Подробную информацию о двух механизмах ползучести см. в разделе «Формулировка ползучести» в «Модифицированной модели Друкера-Прагера/Кэпа», раздел 22.3.2 Руководства пользователя Abaqus Analysis.)
Появится Редактор подопций .
Щелкните стрелку справа от поля Закон и выберите вариант закона ползучести по вашему выбору:
Выберите Деформация , чтобы выбрать степенной закон деформационного упрочнения.
Выберите Время , чтобы выбрать степенной закон временного упрочнения
Выберите SinghM , чтобы выбрать закон типа Сингха-Митчелла.

Выберите User , чтобы задать закон ползучести с помощью пользовательской подпрограммы CREEP.
Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Если выбран параметр Деформация или Время закон ползучести, введите следующие данные в таблицу Данные :
A, n и m
9008 CreПоле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Для получения подробной информации о том, как вводить данные, см. «Ввод табличных данных», Раздел 3.2.7.
Для получения подробной информации о том, как вводить данные, см. «Ввод табличных данных», Раздел 3.2.7.Если вы выбрали вариант закона ползучести SinghM , введите следующие данные в таблицу Data :
A, alpha, m и t1
, и .
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Для получения подробной информации о том, как вводить данные, см. «Ввод табличных данных», Раздел 3.2.7.Щелкните OK , чтобы вернуться в диалоговое окно «Редактировать материал «.
Определение пластичности чугуна
Модель пластичности чугуна описывает механическое поведение серого чугуна, материала, микроструктура которого состоит из чешуек графита в стальной матрице. Определение модели включает пластический коэффициент Пуассона и информацию об упрочнении при сжатии и растяжении. См. «Пластичность чугуна», раздел 22.2.10 Руководства пользователя Abaqus Analysis для получения дополнительной информации.
См. «Пластичность чугуна», раздел 22.2.10 Руководства пользователя Abaqus Analysis для получения дополнительной информации.
Для определения пластичности чугуна
В строке меню диалогового окна Редактировать материал выберите .
(Информацию об отображении диалогового окна «Редактировать материал » см. в разделе «Создание или редактирование материала», раздел 12.7.1.)
Включить Использовать данные, зависящие от температуры , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Введите в таблицу Data следующие данные:
Пластический коэффициент Пуассона
Значение пластического «коэффициента Пуассона», , где .
 (Безразмерный.) Значение по умолчанию — .
(Безразмерный.) Значение по умолчанию — .Температура
Температура, .
Поле n
Предопределенные переменные поля.
Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.
Откройте вкладку Compression Hardening и выполните следующие действия:
Включите Используйте зависящие от температуры данные для определения данных, зависящих от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Введите следующие данные в таблицу Data :
Sigmac
Предел текучести при сжатии, .
Epsilonc
Абсолютное значение соответствующей пластической деформации.
 (Первое введенное табличное значение всегда должно быть нулевым.)
(Первое введенное табличное значение всегда должно быть нулевым.)Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.
Откройте вкладку Упрочнение растяжением и выполните следующие действия:
Включите Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Введите в таблицу Data следующие данные:
Sigmat
Предел текучести при одноосном растяжении, .

Эпсилон
Соответствующая пластическая деформация.(Первое введенное табличное значение всегда должно быть нулем.)
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.
Щелкните OK , чтобы создать материал и закрыть диалоговое окно Edit Material . Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (см. «Просмотр и изменение поведения материала», Раздел 12.7.2, для получения дополнительной информации).
Определение пластичности глины
Модель пластичности глины позволяет указать пластическую часть поведения материала для упруго-пластичных материалов, использующих расширенную модель пластичности Кам-глины. Для получения более подробной информации см. «Модель пластичности критического состояния (глины)», раздел 22.3.4 Руководства пользователя Abaqus Analysis.
Для получения более подробной информации см. «Модель пластичности критического состояния (глины)», раздел 22.3.4 Руководства пользователя Abaqus Analysis.
Определение поведения пластичности глины
Модель пластичности глины Abaqus/Standard описывает неупругую реакцию несвязных грунтов.Эта модель обеспечивает разумное соответствие экспериментально наблюдаемому поведению насыщенных глин. Вы можете определить поведение неупругого материала с помощью функции текучести, которая зависит от трех инвариантов напряжения, связанного предположения о течении для определения скорости пластической деформации и теории деформационного упрочнения, которая изменяет размер поверхности текучести в соответствии с неупругой объемной деформацией.
Для получения дополнительной информации см. «Модель пластичности критического состояния (глины)», раздел 22.3.4 Руководства пользователя Abaqus Analysis.
Для определения пластичности глины
В строке меню диалогового окна Edit Material выберите .

(Информацию об отображении диалогового окна Edit Material см. в разделе «Создание или редактирование материала», раздел 12.7.1.)
Щелкните стрелку справа от поля Hardening и выберите Форма закона упрочнения на ваш выбор:
См. «Закон упрочнения» в «Модели пластичности критического состояния (глины)», Раздел 22.3.4 Руководства пользователя Abaqus Analysis для получения дополнительной информации.Если вы выбрали форму закона упрочнения Экспоненциальный , у вас есть возможность ввести значение для Intercept . Этот параметр соответствует точке пересечения линии первичной консолидации с осью коэффициента пустотности на графике коэффициента пустотности в зависимости от логарифма напряжения давления.
Если вы укажете значение для Intercept , Abaqus проигнорирует любое значение, указанное для начального размера поверхности текучести, , в таблице Data .
Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.

Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Если выбрана форма закона упрочнения Экспоненциальный , введите в таблицу Data следующие данные:
Log Plas Bulk Mod
Логарифмический объемный модуль пластичности, (безразмерный).
Коэффициент напряжения
Коэффициент напряжения в критическом состоянии, M .
Начальный размер Yld Surf Size
Начальный размер поверхности текучести (единицы FL 2 ). Abaqus игнорирует этот элемент данных, если вы указали значение для Intercept .
Wet Yld Surf Size
Параметр, определяющий размер поверхности текучести на «мокрой» стороне критического состояния, . Если это значение опущено или установлено равным нулю, значение 1.
 предполагается 0.
предполагается 0.Отношение напряжения течения
Отношение напряжения течения при трехосном растяжении к напряжению течения при трехосном сжатии, K . . Если это значение оставлено пустым или установлено равным нулю, предполагается значение 1,0.
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Для получения подробной информации о том, как вводить данные, см. «Ввод табличных данных», Раздел 3.2.7.Если выбрана форма закона упрочнения Табличная , введите в таблицу Данные следующие данные:
Init Vol Plas Strain
Начальная объемная пластическая деформация, соответствующая .
Wet Yld Surf Size
Параметр, определяющий размер поверхности текучести на «мокрой» стороне критического состояния, .Если это значение опущено или установлено равным нулю, предполагается значение 1,0.

Отношение напряжения течения
Отношение напряжения течения при трехосном растяжении к напряжению течения при трехосном сжатии, K . . Если это значение оставлено пустым или установлено равным нулю, предполагается значение 1,0.
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Для получения подробной информации о том, как вводить данные, см. «Ввод табличных данных», Раздел 3.2.7.Если вы выбрали табличную форму закона упрочнения, выберите в меню кусочно-линейное упрочнение/размягчение поверхности текучести пластичности Cam-clay. Подробные инструкции см. в разделе «Определение затвердевания глины для модели пластичности глины».
Щелкните OK , чтобы создать материал и закрыть диалоговое окно Edit Material . Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (см.
 «Просмотр и изменение поведения материала», Раздел 12.7.2, для получения дополнительной информации).
«Просмотр и изменение поведения материала», Раздел 12.7.2, для получения дополнительной информации).
Определение упрочнения глины для модели пластичности глины
Редактор подопций позволяет определить кусочно-линейное упрочнение/размягчение поверхности текучести пластичности Cam-clay. Для получения дополнительной информации об этой форме закона упрочнения см. раздел «Кусочно-линейная форма» в «Модель пластичности критического состояния (глины)», раздел 22.3.4 Руководства пользователя Abaqus Analysis.
Определение затвердевания глины
Создайте модель материала, как описано в разделе «Определение поведения пластичности глины».
В меню диалогового окна Edit Material выберите Clay Hardening .
Появится редактор подопций .
Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.

Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
В таблицу Данные введите следующие данные:
Предел текучести
Значение напряжения гидростатического давления при текучести, .
Vol Plas Strain
Абсолютное значение соответствующей объемной пластической деформации.
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data .Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.Щелкните OK , чтобы вернуться в диалоговое окно «Редактировать материал «.
Определение пластичности бетона при повреждении
Модель пластичности бетона при повреждении предоставляет общие возможности для моделирования бетона и других квазихрупких материалов во всех типах конструкций.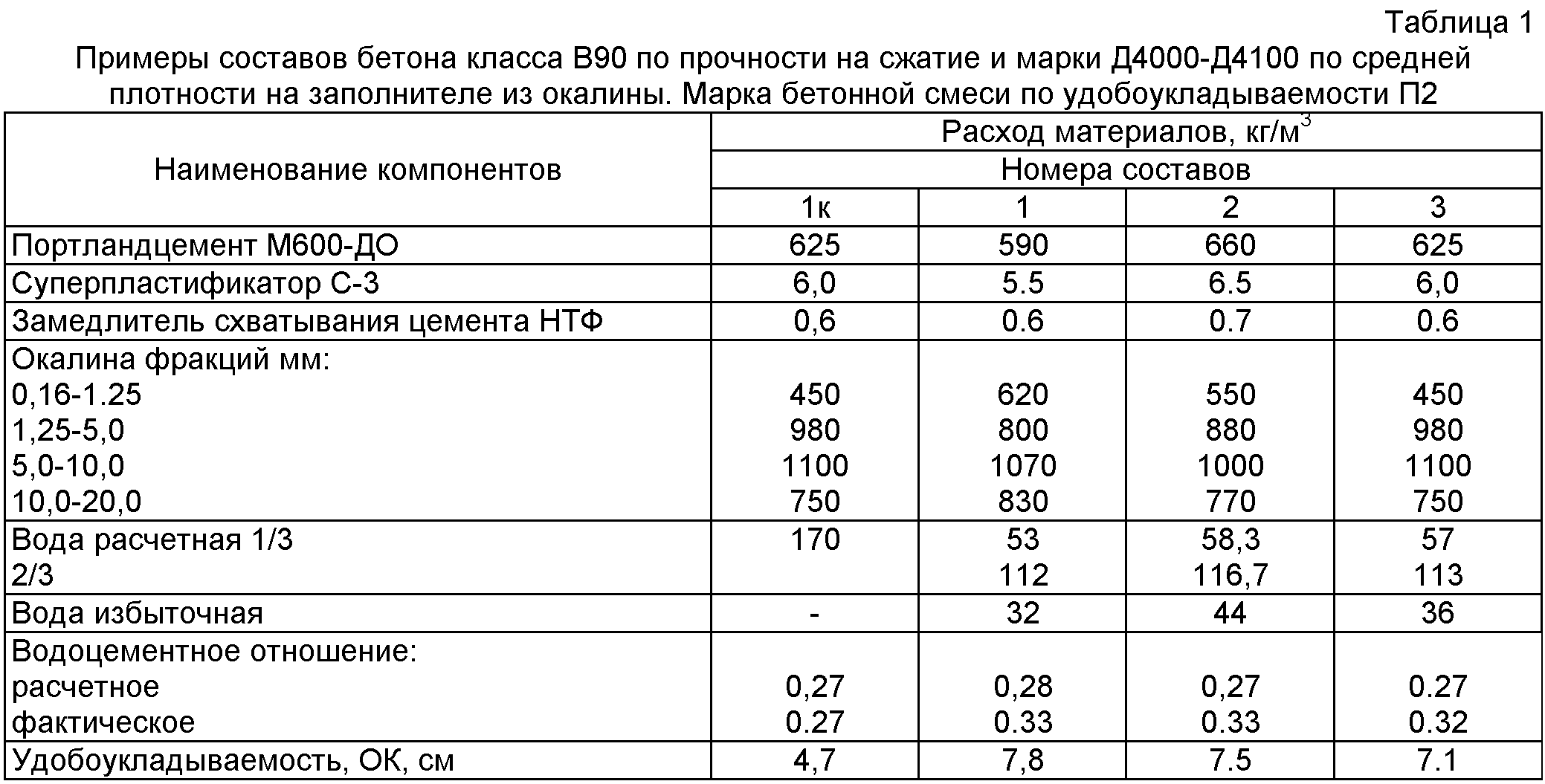 В этой модели используются понятия изотропной поврежденной упругости в сочетании с изотропной пластичностью при растяжении и сжатии для представления неупругого поведения бетона.Дополнительную информацию см. в разделе «Поврежденная пластичность бетона», раздел 22.6.3 Руководства пользователя Abaqus Analysis.
В этой модели используются понятия изотропной поврежденной упругости в сочетании с изотропной пластичностью при растяжении и сжатии для представления неупругого поведения бетона.Дополнительную информацию см. в разделе «Поврежденная пластичность бетона», раздел 22.6.3 Руководства пользователя Abaqus Analysis.
Определение модели пластичности бетона при повреждении
Модель пластичности бетона при повреждении основана на допущении скалярного (изотропного) повреждения и предназначена для приложений, в которых бетон подвергается произвольным условиям нагружения, включая циклическое нагружение. Модель учитывает ухудшение упругой жесткости, вызванное пластическим деформированием как при растяжении, так и при сжатии.Он также учитывает эффекты восстановления жесткости при циклических нагрузках.
Для получения дополнительной информации см. «Поврежденная пластичность бетона», раздел 22.6.3 Руководства пользователя Abaqus Analysis.
Для определения пластичности поврежденного бетона:
В строке меню диалогового окна Edit Material выберите .

(Информацию об отображении диалогового окна Edit Material см. в разделе «Создание или редактирование материала», Раздел 12.7.1.)
При необходимости щелкните вкладку Plasticity , чтобы отобразить страницу с вкладками Plasticity .
Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Введите в таблицу Данные следующие данные:
Угол расширения
Угол расширения, , в плоскости p – q . Введите значение в градусах.
Эксцентриситет
Эксцентриситет потока, . Эксцентриситет — это небольшое положительное число, определяющее скорость, с которой гиперболический потенциал потока приближается к своей асимптоте.
 Значение по умолчанию .
Значение по умолчанию .fb0/fc0
, отношение начального предела текучести равнодвухосного сжатия к начальному пределу текучести одноосного сжатия.Значение по умолчанию:
Параметр вязкости
Параметр вязкости, используемый для вязко-пластической регуляризации определяющих уравнений бетона в анализах Abaqus/Standard. Этот параметр игнорируется в Abaqus/Explicit. Значение по умолчанию равно . (Единицы .)
Поле n
Предопределенные переменные поля.
Щелкните вкладку Compressive Behavior , чтобы открыть страницу с закладками Compressive Behavior .(Информацию об упрочнении при сжатии см. в разделе «Определение поведения при сжатии» в разделе «Пластичность бетона при повреждении», раздел 22.6.3 Руководства пользователя Abaqus Analysis.)
Включить данные о напряжении являются функцией скорости деформации.
Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.

Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Введите следующие данные в таблицу Данные :
Предел текучести
Предел текучести при сжатии, . (Единицы .)
Неупругая деформация
Неупругая (раздавливающая) деформация, .
Скорость
Скорость неупругой (дробящей) деформации, .(Единицы .)
Поле n
Предопределенные переменные поля.
При желании выберите из меню указать повреждения в табличной форме. (Если вы опускаете данные о повреждениях, модель ведет себя как модель пластичности.) Подробности см. в разделе «Определение повреждений бетона при сжатии».
Щелкните вкладку Поведение при растяжении , чтобы отобразить страницу с вкладками Поведение при растяжении .
 (Информацию о жесткости при растяжении см. в разделе «Определение жесткости при растяжении» в разделе «Пластичность бетона при повреждении», раздел 22.6.3 Руководства пользователя Abaqus Analysis). вход в зависимость послеразрушающее напряжение/растрескивание-деформация.
(Информацию о жесткости при растяжении см. в разделе «Определение жесткости при растяжении» в разделе «Пластичность бетона при повреждении», раздел 22.6.3 Руководства пользователя Abaqus Analysis). вход в зависимость послеразрушающее напряжение/растрескивание-деформация.Выберите Смещение , чтобы определить поведение после растрескивания, введя отношение напряжения после разрушения/растрескивания-смещения.
Выберите GFI , чтобы определить поведение после образования трещин путем ввода напряжения разрушения и энергии разрушения.
Включить Использовать данные, зависящие от скорости деформации , если напряжение после образования трещины зависит от скорости деформации.
Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.

В таблицу Data введите данные, относящиеся к вашему типу , выбранному на шаге 13 (не все из следующих применимы):
Предел текучести
Перемещение из списка вариантов Тип , введите остаточное прямое напряжение после образования трещины, .(Единицы .)
Если вы выбрали GFI из списка опций Введите , введите напряжение отказа, . (Единицы .)
Деформация растрескивания
Деформация прямого растрескивания, .
Смещение
Прямое смещение трещинами, . (Единицы л.)
Энергия разрушения
Энергия разрушения, . (Единицы .)
Скорость
Если вы выбрали Деформация из списка опций Тип , введите скорость деформации при прямом растрескивании, .(Единицы .)
Если вы выбрали Displacement или GFI из списка вариантов Type , введите скорость смещения при прямом растрескивании, .
 (Единицы .)
(Единицы .)Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.При желании выберите из меню, чтобы указать повреждения в виде таблицы.(Если вы опускаете данные о повреждениях, модель ведет себя как модель пластичности.) Подробности см. в разделе «Определение повреждений бетона при растяжении».
Щелкните OK , чтобы создать материал и закрыть диалоговое окно Edit Material . Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (дополнительную информацию см. в разделе «Просмотр и изменение поведения материала», раздел 12.7.2).
Определение повреждения бетона при сжатии
Переменную повреждения при одноосном сжатии можно определить как табличную функцию неупругой (раздавливающей) деформации. Для получения дополнительной информации см. раздел «Определение повреждения и восстановления жесткости» в разделе «Пластичность бетона при повреждении», раздел 22.6.3 Руководства пользователя Abaqus Analysis.
Для получения дополнительной информации см. раздел «Определение повреждения и восстановления жесткости» в разделе «Пластичность бетона при повреждении», раздел 22.6.3 Руководства пользователя Abaqus Analysis.
Для определения повреждения при сжатии
Создайте модель материала, как описано в разделе «Определение модели пластичности поврежденного бетона».
В меню на вкладке Compression Behavior выберите Compression Damage .
Появится редактор подопций .
В поле Восстановление при растяжении введите значение коэффициента восстановления жесткости, который определяет степень восстановления жесткости при растяжении при изменении нагрузки от сжатия к растяжению.
Если , материал полностью восстанавливает жесткость при растяжении; если , восстановления жесткости не происходит. Промежуточные значения приводят к частичному восстановлению жесткости при растяжении. Значение по умолчанию — 0,0.

Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Введите в таблицу Данные следующие данные:
Параметр повреждения
Переменная повреждения при сжатии, .
Неупругая деформация
Неупругая (раздавливающая) деформация, .
Поле n
Предопределенные переменные поля.
Щелкните OK , чтобы вернуться в диалоговое окно Edit Material .
Определение повреждения бетона при растяжении
Переменную повреждения при одноосном растяжении можно определить как табличную функцию деформации при растрескивании или смещения при растрескивании. пластичность», раздел 22.6.3 Руководства пользователя Abaqus Analysis.
пластичность», раздел 22.6.3 Руководства пользователя Abaqus Analysis.
Для определения повреждения при растяжении
Создайте модель материала, как описано в разделе «Определение модели пластичности поврежденного бетона».
В меню на вкладке Поведение при растяжении выберите Повреждение при растяжении .
Появится редактор подопций .
Щелкните стрелку справа от поля Введите и выберите метод определения переменной повреждения при растяжении:
В поле Восстановление сжатия введите значение коэффициента восстановления жесткости который определяет величину жесткости на сжатие, которая восстанавливается при изменении нагрузки от растяжения к сжатию.
Если , материал полностью восстанавливает жесткость на сжатие; если , восстановления жесткости не происходит. Промежуточные значения приводят к частичному восстановлению жесткости на сжатие.
 Значение по умолчанию равно , что соответствует допущению о том, что по мере закрытия трещин на жесткость при сжатии не влияет повреждение при растяжении.
Значение по умолчанию равно , что соответствует допущению о том, что по мере закрытия трещин на жесткость при сжатии не влияет повреждение при растяжении.Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
В таблицу Data введите данные, относящиеся к вашему типу , выбранному на шаге 3 (не все из следующих будут применимы):
Параметр повреждения
Деформация растрескивания
Деформация прямого растрескивания, .
Смещение
Прямое смещение трещинами, . (Единицы л.)
Поле n
Предопределенные переменные поля.
Щелкните OK , чтобы вернуться в диалоговое окно Edit Material .

Определение смазанных трещин в бетоне
Модель смазанных трещин в бетоне можно использовать для определения свойств обычного бетона за пределами диапазона упругости в анализе Abaqus/Standard.Дополнительную информацию см. в разделе «Размытые трещины в бетоне», раздел 22.6.1 Руководства пользователя Abaqus Analysis.
Задание модели растрескивания бетона с размазыванием
Модель растрескивания бетона с размазыванием позволяет определить поведение бетона при относительно монотонных нагрузках при довольно низких всесторонних давлениях. Abaqus предполагает, что растрескивание является наиболее важным аспектом поведения, и представление растрескивания и поведения после растрескивания доминирует в моделировании. Дополнительную информацию см. в разделе «Размазанные трещины в бетоне», раздел 22.6.1 Руководства пользователя Abaqus Analysis.
Чтобы определить размазанные трещины в бетоне:
В строке меню диалогового окна Edit Material выберите .

(Информацию об отображении диалогового окна «Редактировать материал» см. в разделе «Создание или редактирование материала», раздел 12.7.1.)
Включить Использовать данные, зависящие от температуры .
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Введите следующие данные в таблицу Данные :
Напряжение сжатия
Абсолютное значение напряжения сжатия. (Единицы FL 2 .)
Пластическая деформация
Абсолютное значение пластической деформации. Первая точка напряжения-деформации, заданная для каждого значения переменной температуры и поля, должна быть при нулевой пластической деформации и будет определять начальный предел текучести для этой переменной температуры и поля.

Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.Выберите из меню, чтобы смоделировать поведение после разрушения для прямой деформации через трещины. Дополнительные сведения см. в разделе «Определение жесткости при растяжении для модели растрескивания бетона».
При желании выберите в меню, как будет уменьшаться сдвиговая жесткость по мере растрескивания бетона.Подробности см. в разделе «Определение удерживания сдвига для модели растрескивания бетона».
При желании выберите в меню форму поверхности разрушения. Дополнительные сведения см. в разделе «Определение формы поверхности разрушения для модели растрескивания бетона».
Щелкните OK , чтобы создать материал и закрыть диалоговое окно Edit Material .
 Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (см. «Просмотр и изменение поведения материала», Раздел 12.7.2, для получения дополнительной информации).
Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (см. «Просмотр и изменение поведения материала», Раздел 12.7.2, для получения дополнительной информации).
Определение жесткости при растяжении для модели растрескивания бетона с размытием
Можно смоделировать поведение после разрушения для прямой деформации через трещины с помощью усиления при растяжении, что позволяет определить поведение смягчения деформации для бетона с трещинами. Такое поведение также позволяет простым способом моделировать эффекты взаимодействия арматуры с бетоном.
Жесткость при растяжении можно указать с помощью соотношения напряжения и деформации после разрушения или с помощью критерия растрескивания энергии разрушения.Дополнительную информацию см. в разделе «Усиление жесткости при растяжении» в разделе «Размазанные трещины в бетоне», раздел 22.6.1 Руководства пользователя Abaqus Analysis.
Для модели растрескивания бетона требуется информация о жесткости при растяжении.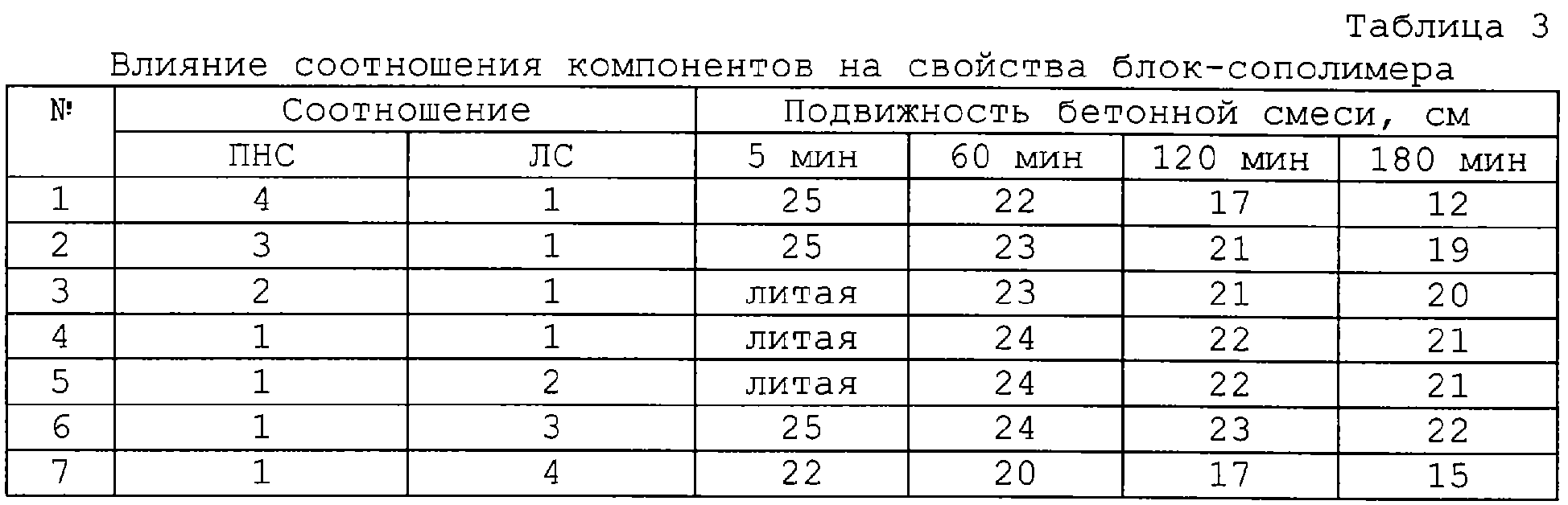
Для определения жесткости при растяжении:
Создайте модель материала, как описано в разделе «Задание модели растрескивания бетона».
В меню выберите Усиление натяжения .
Появится редактор подопций .
Щелкните стрелку справа от поля Введите и выберите метод определения поведения после образования трещин: .
Выберите Деформация , чтобы напрямую ввести зависимость напряжения-деформации после разрушения.
Включить Используйте зависящие от температуры данные для определения данных, зависящих от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
В таблицу Data введите данные, относящиеся к вашему типу , выбранному на шаге 3 (не все из следующих будут применимы):
Disp
прочность после растрескивания дает нулевое напряжение.
 (Единицы л.)
(Единицы л.)sigma/sigma_c
Отношение остаточного напряжения к напряжению при растрескивании.
epsilon-epsilon_c
Абсолютное значение прямой деформации за вычетом прямой деформации при растрескивании.
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Для получения подробной информации о том, как вводить данные, см. «Ввод табличных данных», Раздел 3.2.7.Щелкните OK , чтобы вернуться в диалоговое окно «Редактировать материал «.
Определение устойчивости к сдвигу для модели размазанного растрескивания бетона
По мере растрескивания бетона его жесткость при сдвиге уменьшается. Вы можете определить этот эффект, задав уменьшение модуля сдвига в зависимости от напряжения раскрытия трещины. Также можно указать приведенный модуль сдвига для закрытых трещин. См. раздел «Сохранение трещин при сдвиге» в разделе «Размазанные трещины в бетоне», раздел 22.6.1 Руководства пользователя Abaqus Analysis для получения дополнительной информации.
См. раздел «Сохранение трещин при сдвиге» в разделе «Размазанные трещины в бетоне», раздел 22.6.1 Руководства пользователя Abaqus Analysis для получения дополнительной информации.
Если вы не задаете сопротивление сдвигу для модели размазанного растрескивания бетона, Abaqus/Standard автоматически предполагает, что реакция на сдвиг не зависит от растрескивания (полное сохранение сдвига). Это допущение часто бывает разумным: во многих случаях общий отклик не сильно зависит от степени задержки сдвига.
Чтобы определить устойчивость к сдвигу:
Создайте модель материала, как описано в разделе «Указание модели растрескивания бетона с размытием».
В меню выберите Удержание при сдвиге .
Появится редактор подопций .
Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .

Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Введите следующие данные в таблицу Data :
Rho_close
Множитель, определяющий модуль сдвига закрытых трещин как часть модуля упругого сдвига бетона без трещин. Значение по умолчанию — 1,0.
Eps_max
Максимальное прямое напряжение поперек трещины, . Значение по умолчанию — очень большое число (полное сохранение сдвига).
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.Щелкните OK , чтобы вернуться в диалоговое окно «Редактировать материал «.
Определение формы поверхности разрушения для модели размазанного растрескивания бетона
Для определения формы поверхности разрушения можно указать коэффициенты разрушения. Если вы не задаете форму поверхности отказа, Abaqus использует значения по умолчанию, перечисленные ниже.
Если вы не задаете форму поверхности отказа, Abaqus использует значения по умолчанию, перечисленные ниже.
Чтобы указать коэффициенты отказов:
Создайте модель материала, как описано в разделе «Указание модели растрескивания бетона».
В меню выберите Коэффициенты отказов .
Появится редактор подопций .
Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Введите следующие данные в таблицу Данные :
Отношение 1
Отношение предельного напряжения при двухосном сжатии к предельному напряжению при одноосном сжатии.Значение по умолчанию — 1,16.

Отношение 2
Абсолютное значение отношения одноосного растягивающего напряжения при разрушении к одноосному сжимающему напряжению при разрушении. Значение по умолчанию — 0,09.
Отношение 3
Отношение величины главной составляющей пластической деформации при предельном напряжении при двухосном сжатии к пластической деформации при предельном напряжении при одноосном сжатии. Значение по умолчанию — 1,28.
Отношение 4
Отношение значения главного растягивающего напряжения при растрескивании в плоском напряжении, когда другая ненулевая составляющая главного напряжения равна предельному сжимающему напряжению, к напряжению растрескивания при одноосном растяжении.Значение по умолчанию – 1/3.
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.
в разделе «Ввод табличных данных», раздел 3.2.7.Щелкните OK , чтобы вернуться в диалоговое окно «Редактировать материал «.
Определение пластичности разрушаемой пены
Модель разрушаемой пены позволяет определять не только разрушаемую пену, которая обычно используется в качестве структур, поглощающих энергию, но также и другие разрушаемые материалы, отличные от пены.Дополнительную информацию см. в разделе «Модели пластичности разрушаемой пены», раздел 22.3.5 Руководства пользователя Abaqus Analysis.
Указание модели разрушаемой пены
Модель разрушаемой пены можно использовать для моделирования повышенной способности пеноматериала деформироваться при сжатии из-за процессов потери устойчивости клеточных стенок. Эта модель основана на предположении, что результирующая деформация не может быть восстановлена мгновенно и может быть идеализирована как пластическая для кратковременных событий.Дополнительную информацию см. в разделе «Модели пластичности разрушаемой пены», раздел 22.3.5 Руководства пользователя Abaqus Analysis.
в разделе «Модели пластичности разрушаемой пены», раздел 22.3.5 Руководства пользователя Abaqus Analysis.
Чтобы определить модель разрушаемой пены:
В строке меню диалогового окна Edit Material выберите .
(Информацию об отображении диалогового окна «Редактировать материал » см. в разделе «Создание или редактирование материала», раздел 12.7.1.) модель упрочнения:
Выберите Volumetric , чтобы указать модель, которая предполагает, что поверхность текучести контролируется пластической деформацией объемного уплотнения, которой подвергается материал.Объемное упрочнение — единственная модель, доступная для анализа Abaqus/Standard.
Выберите Изотропный , чтобы задать модель, в которой используется поверхность текучести, представляющая собой эллипс с центром в начале координат в плоскости напряжений p – q . Поверхность текучести развивается самоподобным образом, и эта эволюция определяется эквивалентной пластической деформацией.
 Эта модель доступна только для анализа Abaqus/Explicit.
Эта модель доступна только для анализа Abaqus/Explicit.
Включить Используйте зависящие от температуры данные для определения данных, зависящих от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
В таблицу Data введите данные, относящиеся к вашему выбору Закалка из шага 2 (не все из следующих применимы): , ; .Введите отношение начального предела текучести при одноосном сжатии к начальному пределу текучести при гидростатическом сжатии.
Коэффициент гидростатической текучести
Коэффициент текучести при гидростатической нагрузке, ; . Введите отношение предела текучести при гидростатическом растяжении к начальному пределу текучести при гидростатическом сжатии в виде положительного значения.
 Значение по умолчанию — 1,0.
Значение по умолчанию — 1,0.Коэффициент Пуассона для пластмасс
Коэффициент Пуассона для пластмасс, ; .
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.Выберите из меню, чтобы задать данные затвердевания для модели разрушаемой пены. Подробнее см. в разделе «Определение затвердевания разрушаемой пены».
При желании выберите в меню поведение материала в зависимости от скорости деформации. Подробности см. в разделе «Определение зависимости скорости для модели пластичности разрушаемой пены».
Щелкните OK , чтобы создать материал и закрыть диалоговое окно Edit Material . Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (дополнительную информацию см.
 в разделе «Просмотр и изменение поведения материала», раздел 12.7.2).
в разделе «Просмотр и изменение поведения материала», раздел 12.7.2).
Определение отверждения разрушаемой пены
Для завершения определения пластичности разрушаемой пены необходимо предоставить данные об отверждении разрушаемой пены.Дополнительную информацию см. в разделе «Модели пластичности разрушаемой пены», раздел 22.3.5 Руководства пользователя Abaqus Analysis.
Чтобы определить отверждение разрушаемой пены:
Создайте модель материала, как описано в разделе «Указание модели разрушаемой пены».
В меню выберите Дробленая пена для отверждения .
Появится редактор подопций .
Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.

Введите следующие данные в таблицу Data :
Предел текучести
Предел текучести при одноосном сжатии, представленный как положительное значение.
Объемная пластическая деформация
Абсолютное значение соответствующей пластической деформации.(Первое введенное табличное значение всегда должно быть нулем.)
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.Щелкните OK , чтобы вернуться в диалоговое окно «Редактировать материал «.
Определение зависимости скорости деформации для модели пластичности разрушаемой пены
По мере увеличения скорости деформации многие материалы демонстрируют увеличение предела текучести.Для многих разрушаемых вспененных материалов это увеличение предела текучести становится важным, когда скорость деформации находится в диапазоне 0,1–1 в секунду, и может быть очень важным, если скорость деформации находится в диапазоне 10–100 в секунду, как это обычно происходит в высокоэнергетические динамические события.
Дополнительную информацию о зависимости скорости деформации см. в разделах «Модели пластичности разрушаемой пены», раздел 22.3.5 Руководства пользователя Abaqus Analysis, и «Выход в зависимости от скорости», раздел 22.2.3 Руководства пользователя Abaqus Analysis.
Чтобы определить выход в зависимости от скорости:
Создайте модель материала, как описано в разделе «Указание модели дробимой пены».
В меню диалогового окна Edit Material выберите Rate Dependent .
Появится редактор подопций .
Щелкните стрелку справа от поля Упрочнение и выберите метод определения зависимостей упрочнения:
Выберите Степенной закон , чтобы определить коэффициенты предела текучести с помощью закона перенапряжения Купера-Саймондса.
Выберите Табличный , чтобы ввести коэффициенты предела текучести непосредственно в табличной форме в зависимости от эквивалентных скоростей пластической деформации.

Если применимо, включите Использовать данные, зависящие от температуры , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Если применимо, щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Если вы выбрали Power Law из списка параметров Hardening , введите следующие данные в таблицу Data :
Field n
9
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.Если вы выбрали Коэффициент текучести из списка параметров Закалка , введите следующие данные в таблицу Данные :
Эквивалентная скорость пластической деформации
Эквивалентная скорость пластической деформации (или абсолютное значение скорости осевой пластической деформации при одноосном сжатии для модели разрушаемой пены).

Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.Щелкните OK , чтобы вернуться в диалоговое окно «Редактировать материал «.
Определение пластичности Друкера-Прагера
Вы можете определить модель Друкера-Прагера для моделирования фрикционных материалов, которые обычно представляют собой зернистые грунты и горные породы и демонстрируют зависимость текучести от давления. Дополнительную информацию см. в разделе «Расширенные модели Друкера-Прагера», раздел 22.3.1 Руководства пользователя Abaqus Analysis.
Определение модели Друкера-Прагера
Расширенное семейство моделей пластичности Друкера-Прагера описывает поведение гранулированных материалов или полимеров, в которых поведение текучести зависит от эквивалентного напряжения давления.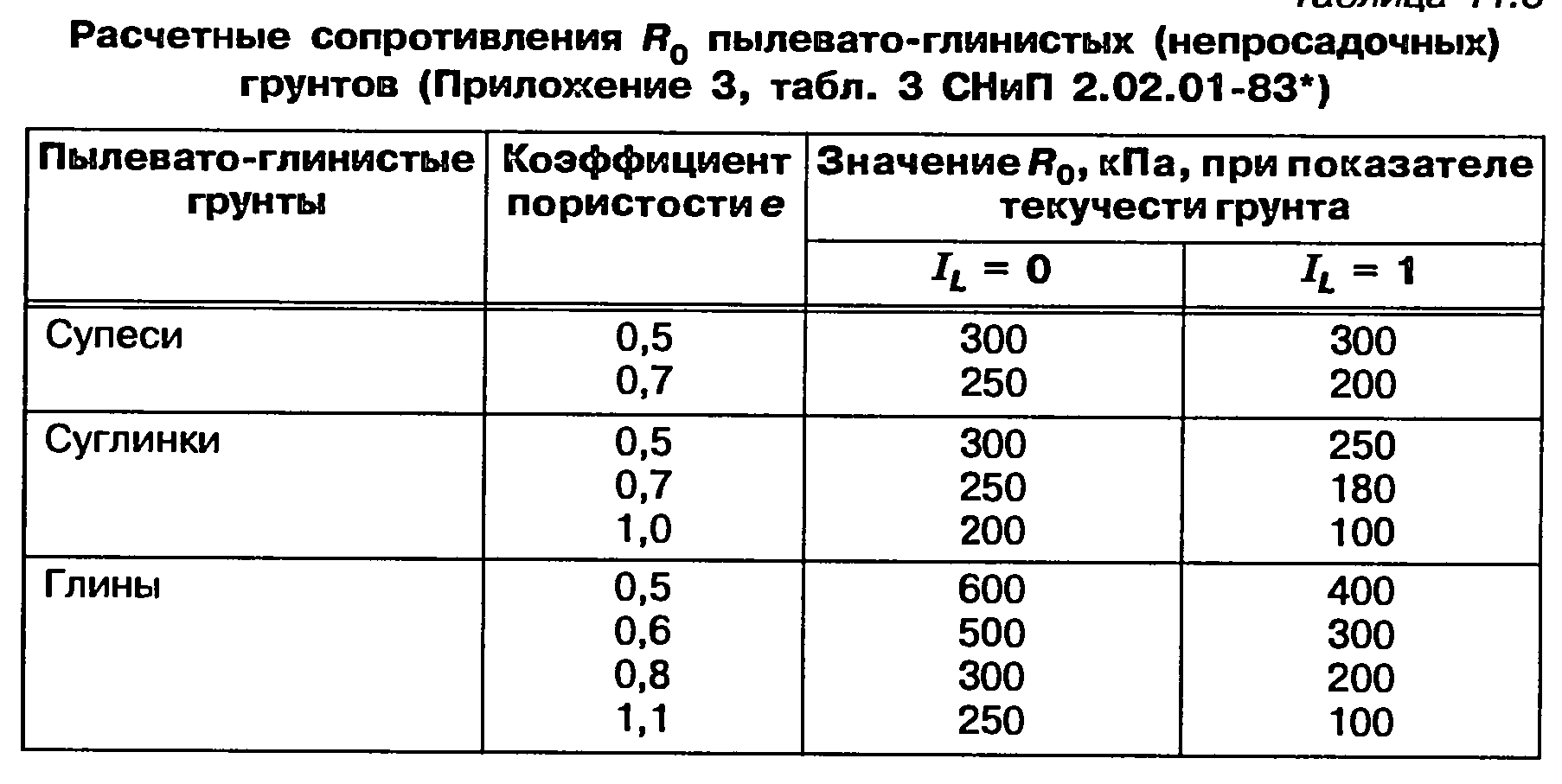 Неупругая деформация иногда может быть связана с механизмами трения, такими как скольжение частиц друг относительно друга. Дополнительную информацию см. в разделе «Расширенные модели Друкера-Прагера», раздел 22.3.1 Руководства пользователя Abaqus Analysis.
Неупругая деформация иногда может быть связана с механизмами трения, такими как скольжение частиц друг относительно друга. Дополнительную информацию см. в разделе «Расширенные модели Друкера-Прагера», раздел 22.3.1 Руководства пользователя Abaqus Analysis.
Чтобы определить модель пластичности Друкера-Прагера:
В строке меню диалогового окна Edit Material выберите .
(Информацию об отображении диалогового окна Edit Material см. в разделе «Создание или редактирование материала», Раздел 12.7.1.)
Щелкните стрелку справа от поля Критерий сдвига и укажите, какой критерий текучести вы хотите определить. Для получения дополнительной информации см. следующие разделы:
Если вы выполняете анализ Abaqus/Standard, введите значение для Эксцентриситет потенциала потока , .
Эксцентриситет — это небольшое положительное число, определяющее скорость, с которой потенциал гиперболического потока приближается к своей асимптоте.
 По умолчанию используется экспоненциальная модель, а если , то для гиперболической модели устанавливается соответствующий поток.Дополнительную информацию см. в разделе «Расширенные модели Друкера-Прагера», раздел 22.3.1 Руководства пользователя Abaqus Analysis.
По умолчанию используется экспоненциальная модель, а если , то для гиперболической модели устанавливается соответствующий поток.Дополнительную информацию см. в разделе «Расширенные модели Друкера-Прагера», раздел 22.3.1 Руководства пользователя Abaqus Analysis.Если вы выбрали Exponent Form из списка параметров Критерий сдвига , вы можете включить Use Suboption Triaxial Test Data , чтобы запросить, чтобы Abaqus вычислил константы материала из данных трехосных испытаний при различных уровнях всестороннего давления. . См. «Модель общего показателя» в «Расширенных моделях Друкера-Прагера», раздел 22.3.1 Руководства пользователя Abaqus Analysis для получения дополнительной информации.
Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.

В таблице Data введите данные, относящиеся к вашему выбору Критерий сдвига (не все из следующих будут применяться):
Угол трения
из вариантов критерия сдвига , введите угол трения материала, , в плоскости p – t .
Если вы выбрали Гиперболический из списка вариантов Критерий сдвига , введите угол трения материала, при высоком всестороннем давлении в плоскости p – q .
Введите значение в градусах.
Отношение напряжения течения
Отношение напряжения течения при трехосном растяжении к напряжению течения при трехосном сжатии, K . . Если вы оставите это поле пустым или введете значение 0,0, Abaqus использует значение по умолчанию, равное 1.0. Если вы планируете определить поведение ползучести, установите K на 1,0.
Угол расширения
Если вы выбрали Линейный из списка параметров Критерий сдвига , введите угол расширения , в плоскости p – t .

Если вы выбрали Hyperbolic или Exponent Form из списка параметров Критерий сдвига , введите угол расширения, , при высоком всестороннем давлении в плоскости p – q .
Введите значение в градусах.
Начальное растяжение
Начальная прочность на гидростатическое растяжение, . (Единицы FL 2 .)
b
Экспонента b . Чтобы обеспечить выпуклую поверхность текучести, .
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.Выберите из меню, чтобы указать данные упрочнения для модели Друкера-Прагера.Подробнее см. в разделе «Определение усиления Друкера-Прагера».
При желании выберите в меню данные о ползучести для модели Друкера-Прагера. Этот параметр действителен, только если вы выбрали Линейный из списка параметров Критерий сдвига и выполняете анализ Abaqus/Standard.
 Подробнее см. в разделе «Определение ползучести Друкера-Прагера».
Подробнее см. в разделе «Определение ползучести Друкера-Прагера».Если вы включили Использовать подопцию Данные трехосных испытаний на шаге 4, выберите в меню для ввода данных трехосных испытаний.Дополнительные сведения см. в разделе «Указание данных трехосного испытания для модели материала Друкера-Прагера».
Щелкните OK , чтобы создать материал и закрыть диалоговое окно Edit Material . Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (дополнительную информацию см. в разделе «Просмотр и изменение поведения материала», раздел 12.7.2).
Определение усиления по Друкеру-Прагеру
Используйте Редактор подопций , чтобы указать данные по усилению для модели Друкера-Прагера.Для получения дополнительной информации об укреплении Друкера-Прагера см. «Укрепление и зависимость от скорости» в «Расширенных моделях Друкера-Прагера», раздел 22. 3.1 Руководства пользователя Abaqus Analysis.
3.1 Руководства пользователя Abaqus Analysis.
Чтобы определить упрочнение Друкера-Прагера:
Создайте модель материала, как описано в разделе «Определение модели Друкера-Прагера».
В меню диалогового окна Edit Material выберите Drucker Prager Hardening .
Появится редактор подопций .
Выберите тип поведения закалки по вашему выбору.
Эволюция поверхности текучести с пластической деформацией описывается в терминах эквивалентного напряжения , которое можно выбрать в качестве одноосного предела текучести при сжатии , одноосного предела текучести при растяжении или при сдвиге (когезия ) предел текучести
Включите Используйте данные, зависящие от скорости деформации , если вы хотите ввести данные, показывающие значения предела текучести в зависимости от эквивалентной пластической деформации при различных скоростях эквивалентной пластической деформации.

Столбец Rate появляется в таблице Data .
В качестве альтернативы, если вы хотите определить зависимость скорости деформации с помощью коэффициентов предела текучести, вы должны выбрать в меню диалогового окна «Редактировать материал «. Дополнительные сведения см. в разделе «Определение доходности, зависящей от нормы, с помощью коэффициентов предела текучести». Справочную информацию о зависимости от скорости см. в разделе «Доходность в зависимости от скорости», раздел 22.2.3 Руководства пользователя Abaqus Analysis.
Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Введите следующие данные в таблицу Data :
Abs Plastic Strain
Абсолютное значение соответствующей пластической деформации.
 (Первое введенное табличное значение всегда должно быть нулевым.)
(Первое введенное табличное значение всегда должно быть нулевым.)Скорость
Эквивалентная скорость пластической деформации, для которой применяется эта кривая упрочнения.
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.Щелкните OK , чтобы вернуться в диалоговое окно «Редактировать материал «.
Определение ползучести Друкера-Прагера
Вы можете определить классическое «ползучее» поведение материалов, проявляющих пластичность, в соответствии с расширенными моделями Друкера-Прагера в анализе Abaqus/Standard. Поведение ползучести в таких материалах тесно связано с поведением пластичности (через определения потенциалов текучести при ползучести и определения данных испытаний), поэтому в определение материала необходимо включить как пластичность Друкера-Прагера, так и данные упрочнения Друкера-Прагера.
Вводимые данные о ползучести должны соответствовать типу поведения «Упрочнение» , который вы выбираете при определении упрочнения по Друкеру-Прагеру (подробности см. в разделе «Определение упрочнения по Друкеру-Прагеру»).
Для получения дополнительной информации см. раздел «Модели ползучести для линейной модели Друкера-Прагера» в разделе «Расширенные модели Друкера-Прагера», раздел 22.3.1 Руководства пользователя Abaqus Analysis.
Для определения ползучести Друкера-Прагера:
Создайте модель материала, как описано в разделе «Определение модели Друкера-Прагера».”
В меню диалогового окна Edit Material выберите Drucker Prager Creep .
Появится редактор подопций .
Щелкните стрелку справа от поля Закон и выберите вариант закона ползучести по вашему выбору:
Выберите Деформация , чтобы выбрать степенной закон деформационного упрочнения.

Выберите Время , чтобы выбрать степенной закон временного упрочнения
Выберите SinghM , чтобы выбрать закон типа Сингха-Митчелла.
Выберите User , чтобы задать закон ползучести с помощью пользовательской подпрограммы CREEP.
Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Если выбран параметр Деформация или Время закон ползучести, введите следующие данные в таблицу Данные :
A, n и m
9008 CreПоле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Для получения подробной информации о том, как вводить данные, см. «Ввод табличных данных», Раздел 3.2.7.
Если выбран вариант закона ползучести SinghM , введите следующие данные в таблицу Data :
A, alpha, m и t1
м .
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Для получения подробной информации о том, как вводить данные, см. «Ввод табличных данных», Раздел 3.2.7.Щелкните OK , чтобы вернуться в диалоговое окно «Редактировать материал «.
Задание данных трехосных испытаний для модели материала Друкера-Прагера
Abaqus может использовать данные трехосных испытаний для калибровки параметров материала, которые определяют форму экспоненты пластичности Друкера-Прагера.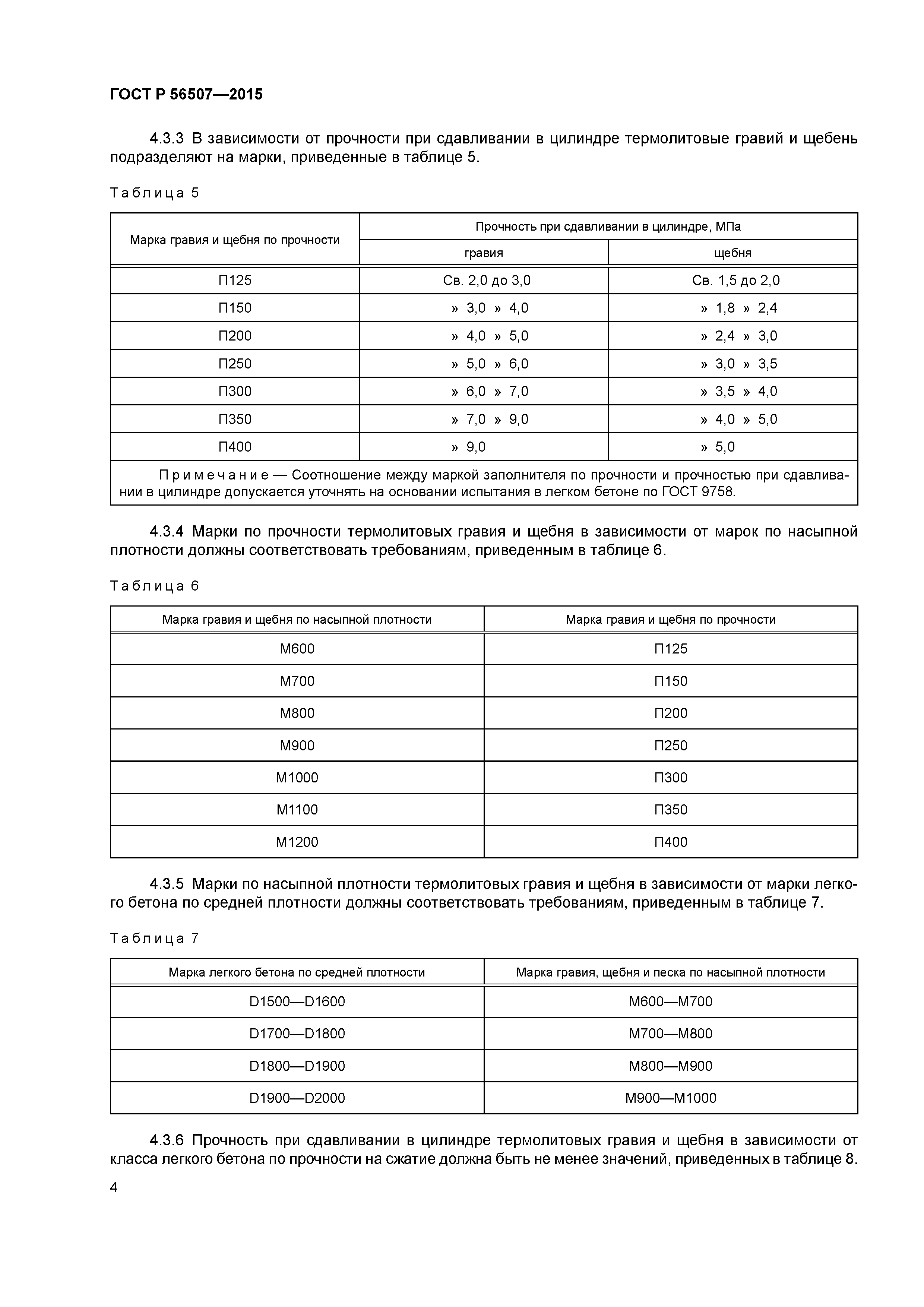 Для получения дополнительной информации см. «Модель общей экспоненты» в «Расширенных моделях Друкера-Прагера», раздел 22.3.1 Руководства пользователя Abaqus Analysis.
Для получения дополнительной информации см. «Модель общей экспоненты» в «Расширенных моделях Друкера-Прагера», раздел 22.3.1 Руководства пользователя Abaqus Analysis.
Для ввода данных трехосного испытания:
Создайте модель материала, как описано в разделе «Определение модели Друкера-Прагера».
В меню диалогового окна Edit Material выберите Triaxial Test Data .
Появится редактор подопций .
Введите значения для Константа материала a , Константа материала b и Константа материала pt , если они известны и зафиксированы на входном значении.Кроме того, вы можете оставить одно или несколько полей пустыми, если хотите, чтобы Abaqus откалибровал значения по данным трехосного теста.
Введите следующие данные в таблицу Data :
Всестороннее напряжение
Знак и величина всестороннего напряжения, .
Нагрузка Dirn Напряжение
Знак и величина напряжения в направлении нагрузки, .
Подробную информацию о том, как вводить данные, см. в разделе 3 «Ввод табличных данных».2.7.
Щелкните OK , чтобы вернуться в диалоговое окно «Редактировать материал «.
Определение пластичности Мора-Кулона
Модель пластичности Мора-Кулона можно использовать для инженерно-геологических приложений. В модели используется классический критерий текучести Мора-Колумба: прямая линия в меридиональной плоскости и неправильное шестиугольное сечение в девиаторной плоскости. Однако модель Abaqus Мора-Кулона имеет полностью гладкий потенциал потока вместо классической гексагональной пирамиды: потенциал потока представляет собой гиперболу в меридиональной плоскости и использует гладкий девиаторный участок, предложенный Ментреем и Уилламом.Дополнительную информацию см. в разделе «Пластичность Мора-Кулона», раздел 22.3.3 Руководства пользователя Abaqus Analysis.
Для определения пластичности Кулона-Мора
В строке меню диалогового окна Edit Material выберите .

(Информацию об отображении диалогового окна «Редактировать материал » см. в разделе «Создание или редактирование материала», раздел 12.7.1.) страница с вкладками.
Выберите о том, как вы хотите определить Deviatoric Excentricity , E :
9098 E :Выбор CALED CALUED по умолчанию , чтобы позволить ABAQUS рассчитать девиационному эксцентриситету, как, где находится угол трения MOHR-Coulomb , который вы указать в таблице Data .
Выберите Укажите и введите значение девиаторного эксцентриситета в соответствующем поле. Диапазон значений e может быть .
Введите значение для Меридиональный эксцентриситет , .
Меридиональный эксцентриситет — это небольшое положительное число, определяющее скорость, с которой потенциал потока приближается к своей асимптоте.
Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.

Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Внесите в таблицу Данные следующие данные:
Угол трения
Угол трения, , при высоком всестороннем давлении в p – плоскости. Введите значение в градусах.
Угол расширения
Угол расширения, , при высоком всестороннем давлении в p – плоскости. Введите значение в градусах.
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data .Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.Щелкните вкладку Cohesion , чтобы отобразить страницу с вкладками Cohesion .

Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Введите следующие данные в таблицу Data :
Abs Plastic Strain
Абсолютное значение соответствующей пластической деформации. (Первое введенное табличное значение всегда должно быть нулем.)
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Для получения подробной информации о том, как вводить данные, см. «Ввод табличных данных», Раздел 3.2.7.При необходимости включите Укажите отсечку по натяжению и щелкните вкладку Отсечка по натяжению , чтобы указать данные напряжения отсечки по натяжению, чтобы ограничить несущую способность модели материала вблизи области растяжения.

Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Введите следующие данные в таблицу Данные :
Напряжение отсечки при растяжении
Предел текучести при одноосном растяжении, .
Пластическая деформация при растяжении
Соответствующая пластическая деформация. (Первое введенное табличное значение всегда должно быть нулем.)
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data .Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3. 2.7.
2.7.Щелкните OK , чтобы создать материал и закрыть диалоговое окно Edit Material . Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (дополнительную информацию см. в разделе «Просмотр и изменение поведения материала», раздел 12.7.2).
Определение закона ползучести
Если вы выполняете анализ Abaqus/Standard, вы можете определить классическое девиаторное поведение ползучести металла, либо указав пользовательскую подпрограмму CREEP, либо задав параметры для некоторых простых законов ползучести.Дополнительную информацию см. в разделе «Пластичность, зависящая от скорости: ползучесть и набухание», раздел 22.2.4 Руководства пользователя Abaqus Analysis.
Для определения ползучести:
В строке меню диалогового окна Edit Material выберите .
(Информацию об отображении диалогового окна Edit Material см.
 в разделе «Создание или редактирование материала», Раздел 12.7.1.)
в разделе «Создание или редактирование материала», Раздел 12.7.1.)Щелкните стрелку справа от поля Law и выберите закон ползучести на ваш выбор.Дополнительную информацию см. в разделе «Поведение при ползучести» в разделе «Пластичность, зависящая от скорости: ползучесть и набухание», раздел 22.2.4 Руководства пользователя Abaqus Analysis.
Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Если вы выбрали затвердевание на деформацию или Закон , введите следующие данные в диаграмме Data Таблица:
Уминология энергетического законодательства
У.Н. (Единицы FLT.
 )
)Порядок эквивалентного напряжения
Порядок эквивалентного девиаторного напряжения, n .
Порядок времени
Общий порядок времени, м , для закона ползучести Time-Holdening , или порядок деформации, м , для закона ползучести Strain-Hardening .
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.Если выбран закон ползучести Hyperbolic-Sine , введите в таблицу Data следующие данные:(Единицы T 1 .)
Множитель по закону гиперболы
Множитель по закону гиперболического синуса, B . (Единицы F 1 L 2 .)
Эквивалентный порядок напряжения
Эквивалентный порядок напряжения, n
Энергия активации
5 (Единицы JM 1
Универсальная газовая постоянная
Универсальная газовая постоянная, R .
 (Единицы JM 1 1 .)
(Единицы JM 1 1 .)Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.При желании выберите из меню, чтобы реализовать правила ползучести, заданные конститутивной моделью Окриджской национальной лаборатории. Дополнительную информацию см. в разделе «Использование конститутивной модели Окриджской национальной лаборатории (ORNL) в расчетах пластичности и ползучести».
При необходимости выберите в меню, чтобы указать поведение анизотропной ползучести. Дополнительную информацию см. в разделе «Определение анизотропной текучести и ползучести».
Щелкните OK , чтобы создать материал и закрыть диалоговое окно Edit Material . Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (дополнительную информацию см.
 в разделе «Просмотр и изменение поведения материала», раздел 12.7.2).
в разделе «Просмотр и изменение поведения материала», раздел 12.7.2).
Определение набухания
Пользовательская подпрограмма CREEP («CREEP», раздел 1.1.1 Справочного руководства по пользовательским подпрограммам Abaqus) предоставляет очень общие возможности для реализации вязкопластических моделей, таких как модели ползучести и набухания. Однако вы также можете ввести данные о набухании в табличной форме. Дополнительную информацию см. в разделе «Поведение объемного набухания» в разделе «Пластичность, зависящая от скорости: ползучесть и набухание», раздел 22.2.4 Руководства пользователя Abaqus Analysis.
Определение модели объемного набухания
Как и законы ползучести, законы объемного набухания обычно сложны, и их удобнее всего задавать в пользовательской подпрограмме CREEP.Однако вы также можете ввести табличные данные о набухании в диалоговом окне Edit Material . Дополнительную информацию см. в разделе «Поведение объемного набухания» в разделе «Пластичность, зависящая от скорости: ползучесть и набухание», раздел 22.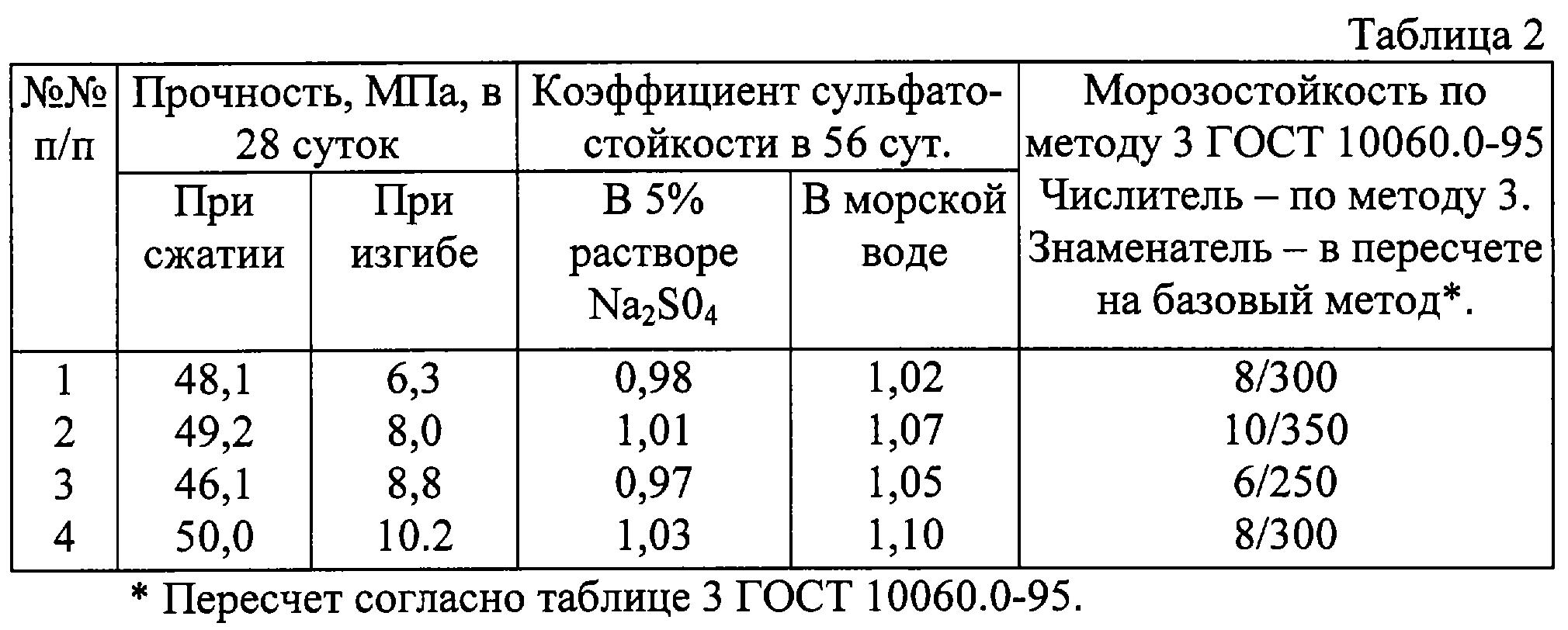 2.4 Руководства пользователя Abaqus Analysis.
2.4 Руководства пользователя Abaqus Analysis.
Чтобы определить набухание:
В строке меню диалогового окна Edit Material выберите .
(Информацию об отображении диалогового окна Edit Material см. в разделе «Создание или редактирование материала», Раздел 12.7.1.)
Щелкните стрелку справа от поля Law и выберите параметр для указания данных о набухании:
Выберите Input для ввода табличных данных в диалоговом окне Edit Material .
Выберите Определяемый пользователем , чтобы определить поведение набухания в пользовательской подпрограмме CREEP
Если вы выбрали Введите на шаге 2, включите Использовать данные, зависящие от температуры температура.
Столбец с меткой Temp появляется в таблице Data .
Если вы выбрали Ввод на шаге 2, щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.

Если вы выбрали Ввод на шаге 2, введите следующие данные в таблицу Данные :
Скорость деформации
Скорость деформации при объемном набухании.
Поле n
Предопределенные переменные поля.
При желании выберите Отношения в меню Подопции для определения анизотропного набухания. Подробнее см. в разделе «Определение анизотропного набухания».
Щелкните OK , чтобы создать материал и закрыть диалоговое окно Edit Material . Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (см. «Просмотр и изменение поведения материала», Раздел 12.7.2, для получения дополнительной информации).
Определение анизотропного набухания
В Редакторе подопций можно указать коэффициенты для определения скорости набухания в каждом направлении материала. Дополнительную информацию см. в разделе «Поведение объемного набухания» в разделе «Пластичность, зависящая от скорости: ползучесть и набухание», раздел 22.2.4 Руководства пользователя Abaqus Analysis.
Дополнительную информацию см. в разделе «Поведение объемного набухания» в разделе «Пластичность, зависящая от скорости: ползучесть и набухание», раздел 22.2.4 Руководства пользователя Abaqus Analysis.
Для определения анизотропного набухания
Создайте модель материала, как описано в разделе «Определение модели объемного набухания.”
В меню диалогового окна Edit Material выберите Ratios .
Появится редактор подопций .
Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Введите следующие данные в таблицу Data :
r11, r22 и r33
Коэффициенты анизотропного набухания, , , и .

Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.Щелкните OK , чтобы вернуться в диалоговое окно «Редактировать материал «.
Определение вязкостного компонента двухслойной модели вязкопластичности
Двухслойная модель вязкопластичности в Abaqus/Standard полезна для моделирования материалов, в которых наблюдаются существенные зависимости поведения от времени, а также пластичности. Для металлов это обычно происходит при повышенных температурах. Эта модель состоит из трех частей: упругой, пластичной и вязкой. Вы можете определить вязкостное поведение материала, выбрав закон ползучести и введя параметры вязкости.Для получения дополнительной информации см. «Двухслойная вязкопластичность», раздел 22. 2.11 Руководства пользователя Abaqus Analysis.
2.11 Руководства пользователя Abaqus Analysis.
Чтобы определить вязкость для двухслойной модели вязкопластичности:
В строке меню диалогового окна Edit Material выберите .
(Информацию об отображении диалогового окна Edit Material см. в разделе «Создание или редактирование материала», Раздел 12.7.1.)
Щелкните стрелку справа от поля Law и выберите Закон ползучести по вашему выбору:
Выберите Деформация , чтобы выбрать степенной закон упрочнения деформации.
Выберите Время , чтобы выбрать степенной закон временной жесткости.
Выберите User , чтобы определить закон ползучести с помощью пользовательской подпрограммы CREEP.

Включить Используйте данные, зависящие от температуры, , чтобы определить данные, зависящие от температуры.
Столбец с меткой Temp появляется в таблице Data .
Щелкните стрелки справа от поля Количество переменных поля , чтобы увеличить или уменьшить количество переменных поля, от которых зависят данные.
Если вы выбрали закон ползучести Strain-Hardening или Time-Holdening , введите следующие данные в таблицу Data :
A
9 Степенной закон (Единицы FLT.)
n
Порядок эквивалентного девиаторного напряжения, n .
м
Полное время или эквивалентный порядок деформации ползучести, м .
f
Дробь, f , определяющая отношение модуля упругости упруго-вязкой сети к полному (мгновенному) модулю.
Поле n
Предопределенные переменные поля.
Возможно, вам придется развернуть диалоговое окно, чтобы увидеть все столбцы в таблице Data . Для получения подробной информации о том, как вводить данные, см. «Ввод табличных данных», Раздел 3.2.7.
Если вы определяете закон ползучести с помощью пользовательской подпрограммы CREEP, введите в таблицу Data следующее: -вязкая сеть к полному (мгновенному) модулю.
Поле n
Предопределенные переменные поля.
Подробную информацию о том, как вводить данные, см. в разделе 3 «Ввод табличных данных».2.7.При необходимости выберите Potential в меню Suboptions для определения анизотропной вязкости. Дополнительные сведения см. в разделе «Определение анизотропной текучести и ползучести».
Щелкните OK , чтобы создать материал и закрыть диалоговое окно Edit Material . Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (см.
 «Просмотр и изменение поведения материала», Раздел 12.7.2, для получения дополнительной информации).
«Просмотр и изменение поведения материала», Раздел 12.7.2, для получения дополнительной информации).
Закон о повреждении путевой плиты на основе модели пластичности поврежденного бетона
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

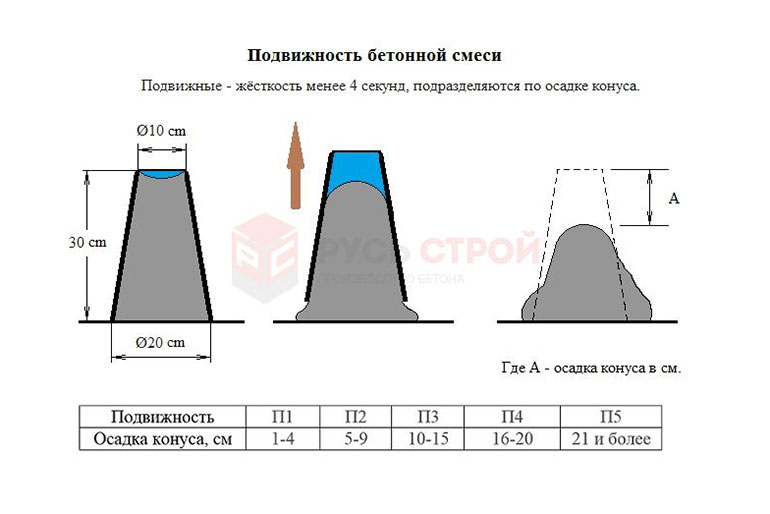 Обычное значение в/ц, как правило, 0,3—0,55. Для реакции гидратации достаточно в/ц менее 0,3, но смесь получается очень густой.
Обычное значение в/ц, как правило, 0,3—0,55. Для реакции гидратации достаточно в/ц менее 0,3, но смесь получается очень густой.
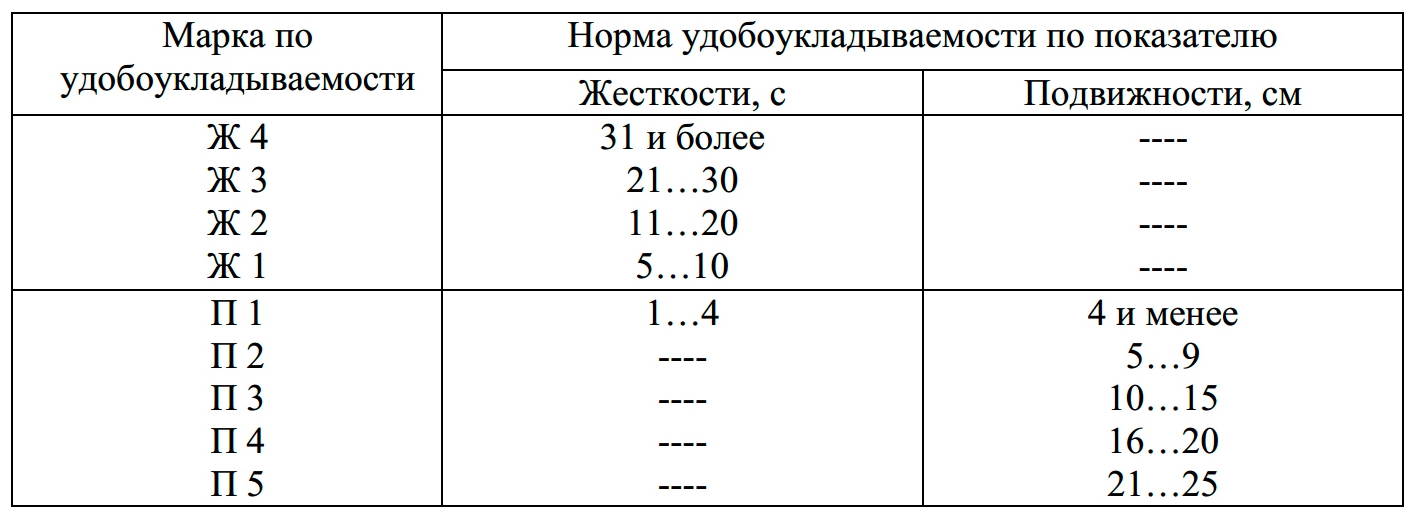
 м.)
м.)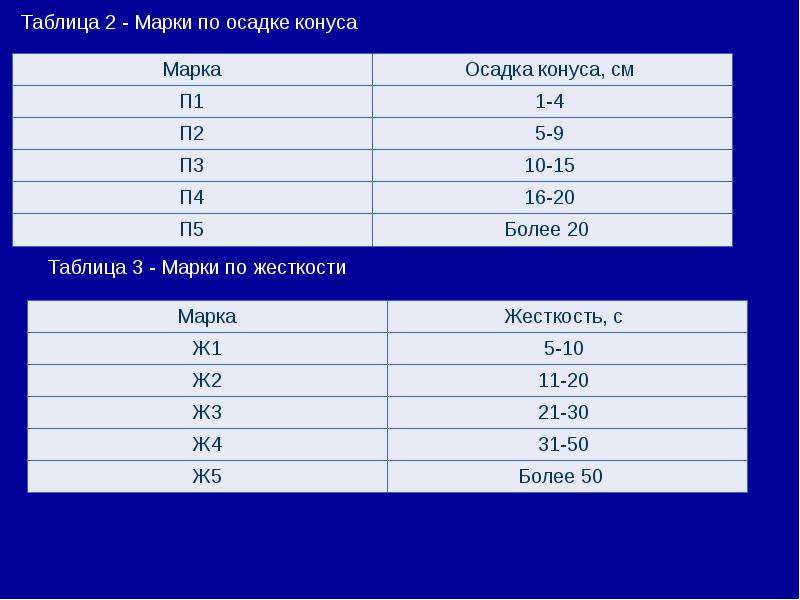 И это реальный способ существенно сэкономить средства.
И это реальный способ существенно сэкономить средства.



 При ненормируемом увеличении этих компонентов друг относительно друга, увеличивается удельная площадь заполнителей и снижается подвижность.
При ненормируемом увеличении этих компонентов друг относительно друга, увеличивается удельная площадь заполнителей и снижается подвижность.
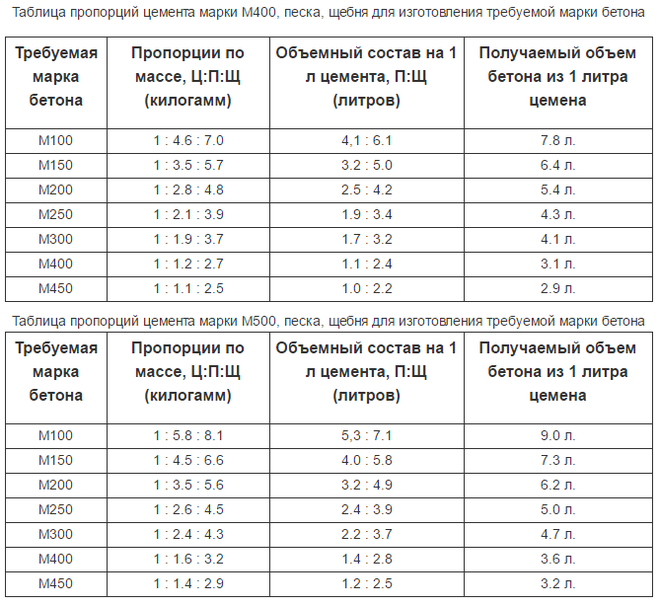 ). Эта смесь требует тщательного вибрирования при укладке и дополнительного физического труда при укладке на большой площади
). Эта смесь требует тщательного вибрирования при укладке и дополнительного физического труда при укладке на большой площади В связи с этим изготовление конструкций из жесткого или сверхжесткого бетона возможно исключительно в заводских условиях;
В связи с этим изготовление конструкций из жесткого или сверхжесткого бетона возможно исключительно в заводских условиях;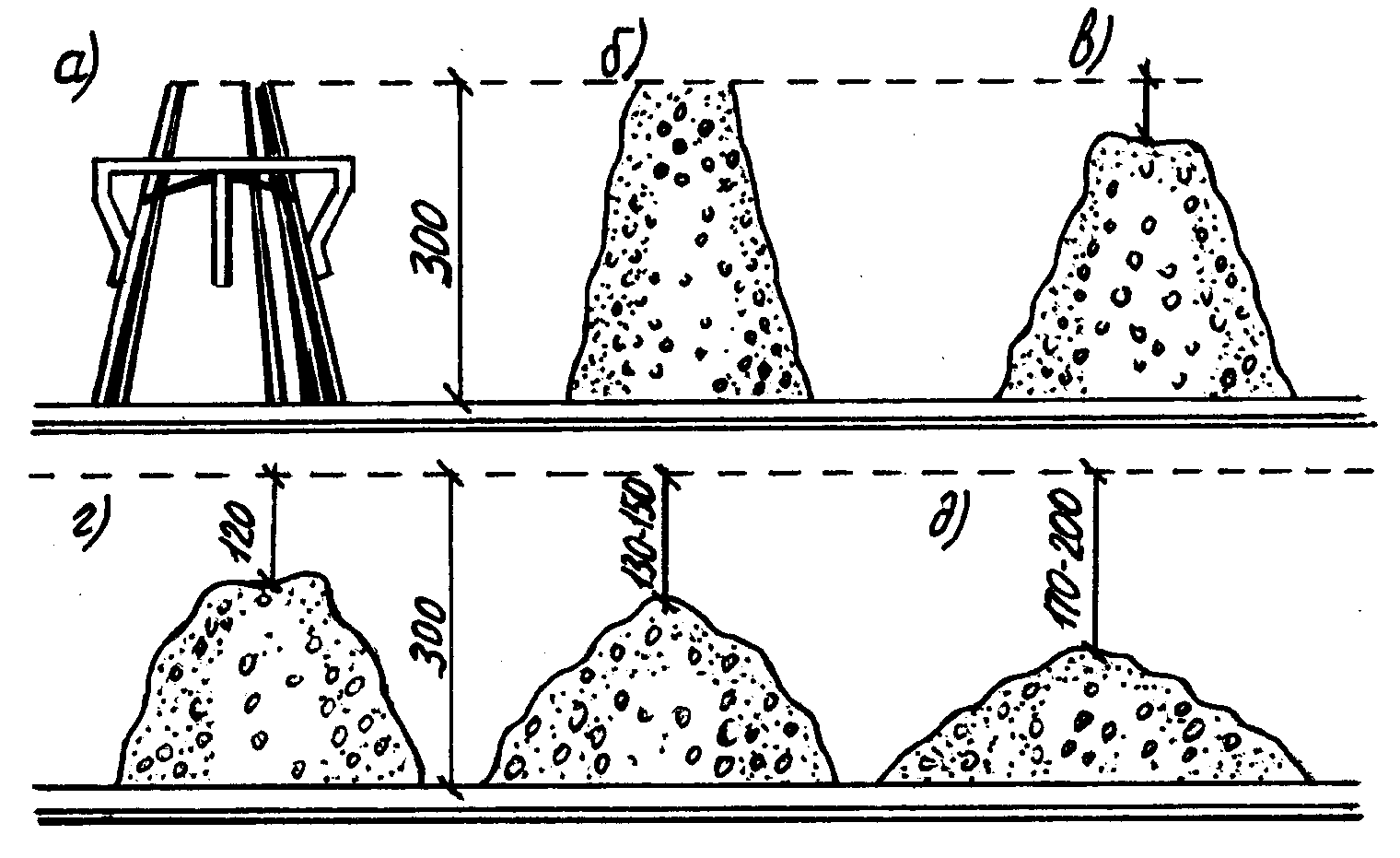
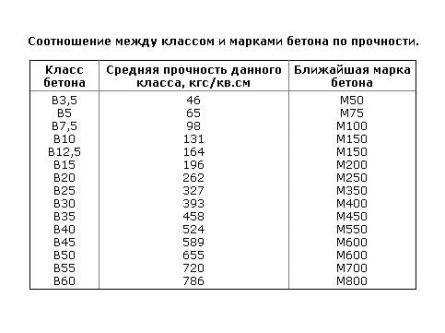
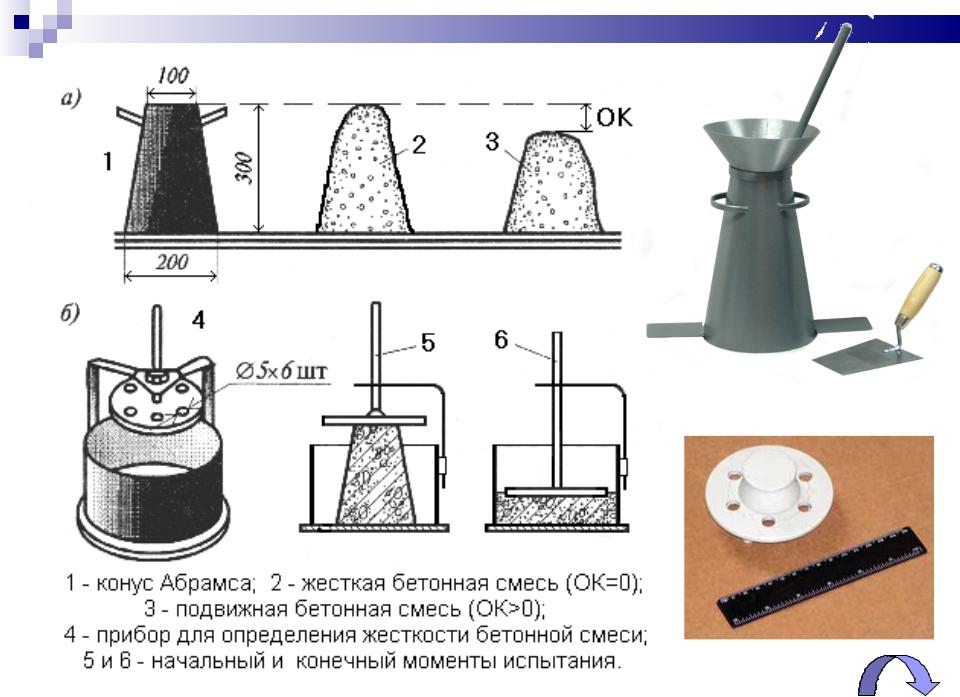 Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.
Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7. Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.
Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.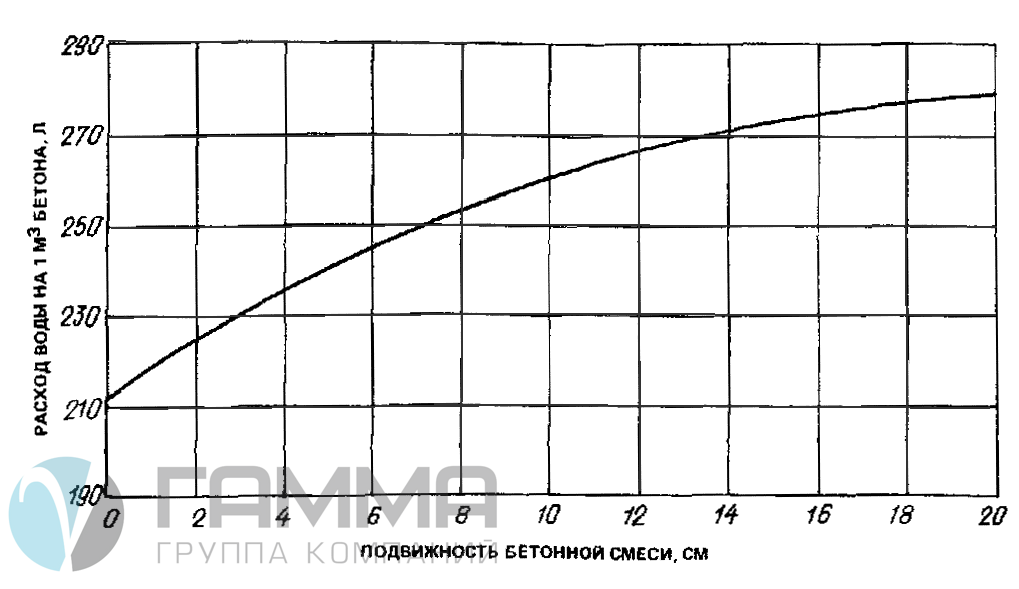
 в разделе «Создание или редактирование материала», раздел 12.7.1.) Комбинированный .
в разделе «Создание или редактирование материала», раздел 12.7.1.) Комбинированный . .
.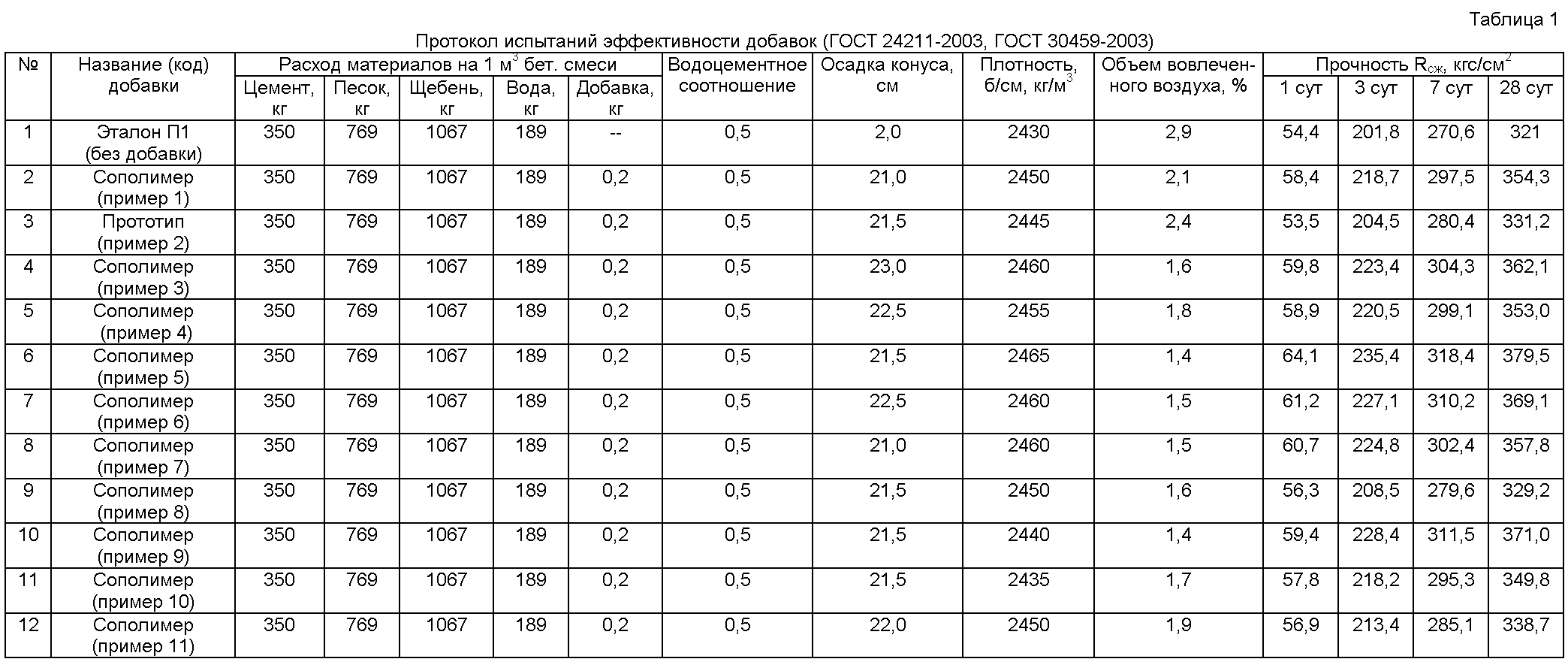
 Дополнительные сведения см. в разделе «Определение компонента изотропного упрочнения нелинейной модели изотропного/кинематического упрочнения».
Дополнительные сведения см. в разделе «Определение компонента изотропного упрочнения нелинейной модели изотропного/кинематического упрочнения».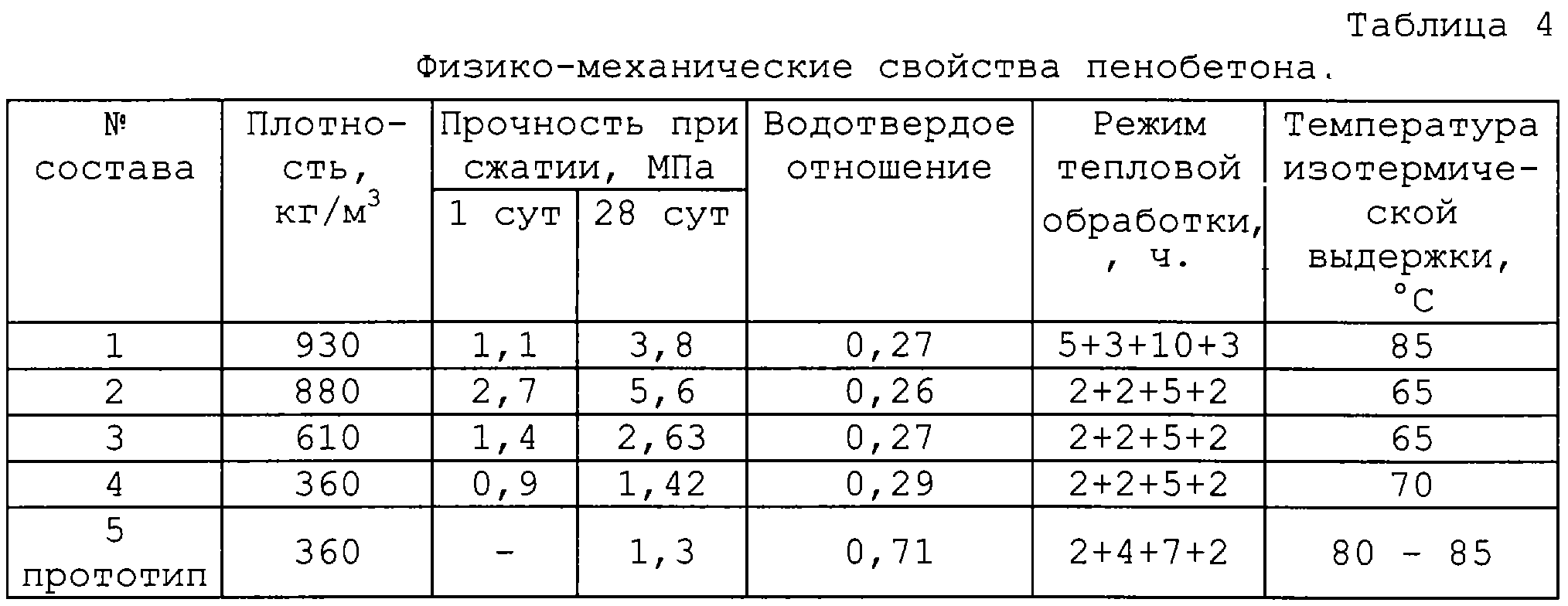

 в разделе «Ввод табличных данных», раздел 3.2.7.
в разделе «Ввод табличных данных», раздел 3.2.7.
 в разделе «Ввод табличных данных», раздел 3.2.7.
в разделе «Ввод табличных данных», раздел 3.2.7.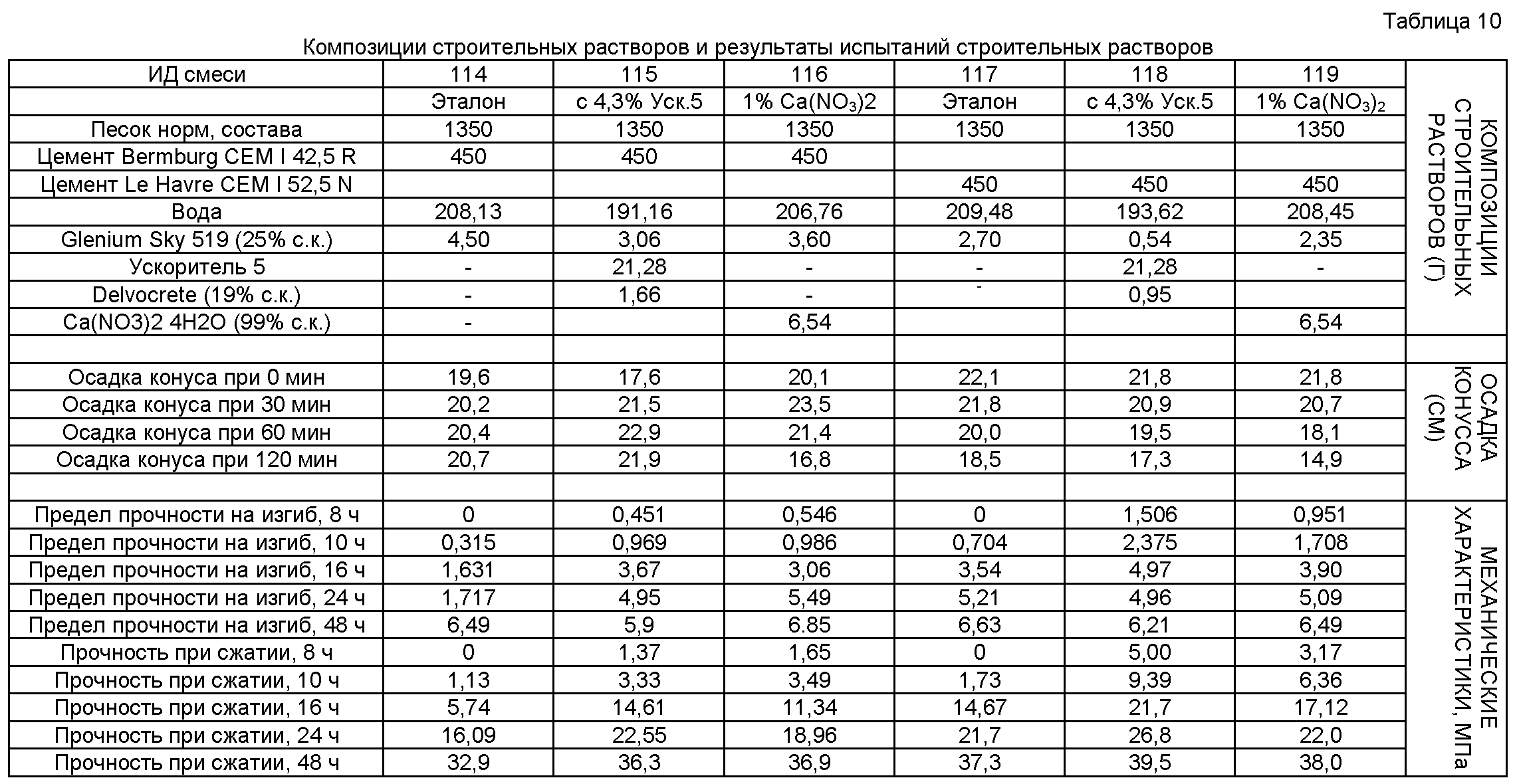 Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.
Подробную информацию о том, как вводить данные, см. в разделе «Ввод табличных данных», раздел 3.2.7.
 3.5 стандарта для ядерной энергетики.
3.5 стандарта для ядерной энергетики.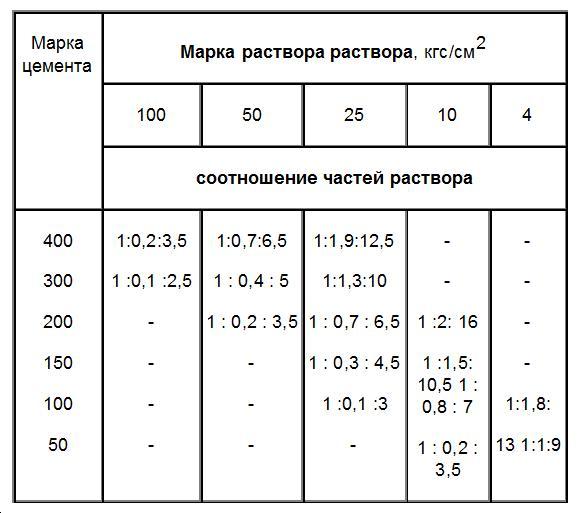
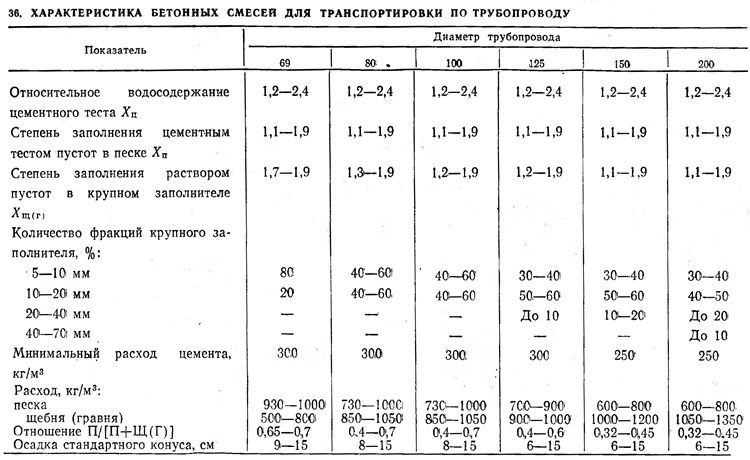 Значение K должно быть таким, чтобы .Если оставить это поле пустым или ввести значение 0,0, Abaqus по умолчанию использует значение 1,0. Если вы включаете свойства ползучести в модель материала, вы должны установить K равным 1,0. Этот параметр применяется только к анализам Abaqus/Standard.
Значение K должно быть таким, чтобы .Если оставить это поле пустым или ввести значение 0,0, Abaqus по умолчанию использует значение 1,0. Если вы включаете свойства ползучести в модель материала, вы должны установить K равным 1,0. Этот параметр применяется только к анализам Abaqus/Standard.
 (Исходное табличное значение должно быть больше нуля, и значения должны увеличиваться с увеличением объемной неупругой деформации.)
(Исходное табличное значение должно быть больше нуля, и значения должны увеличиваться с увеличением объемной неупругой деформации.)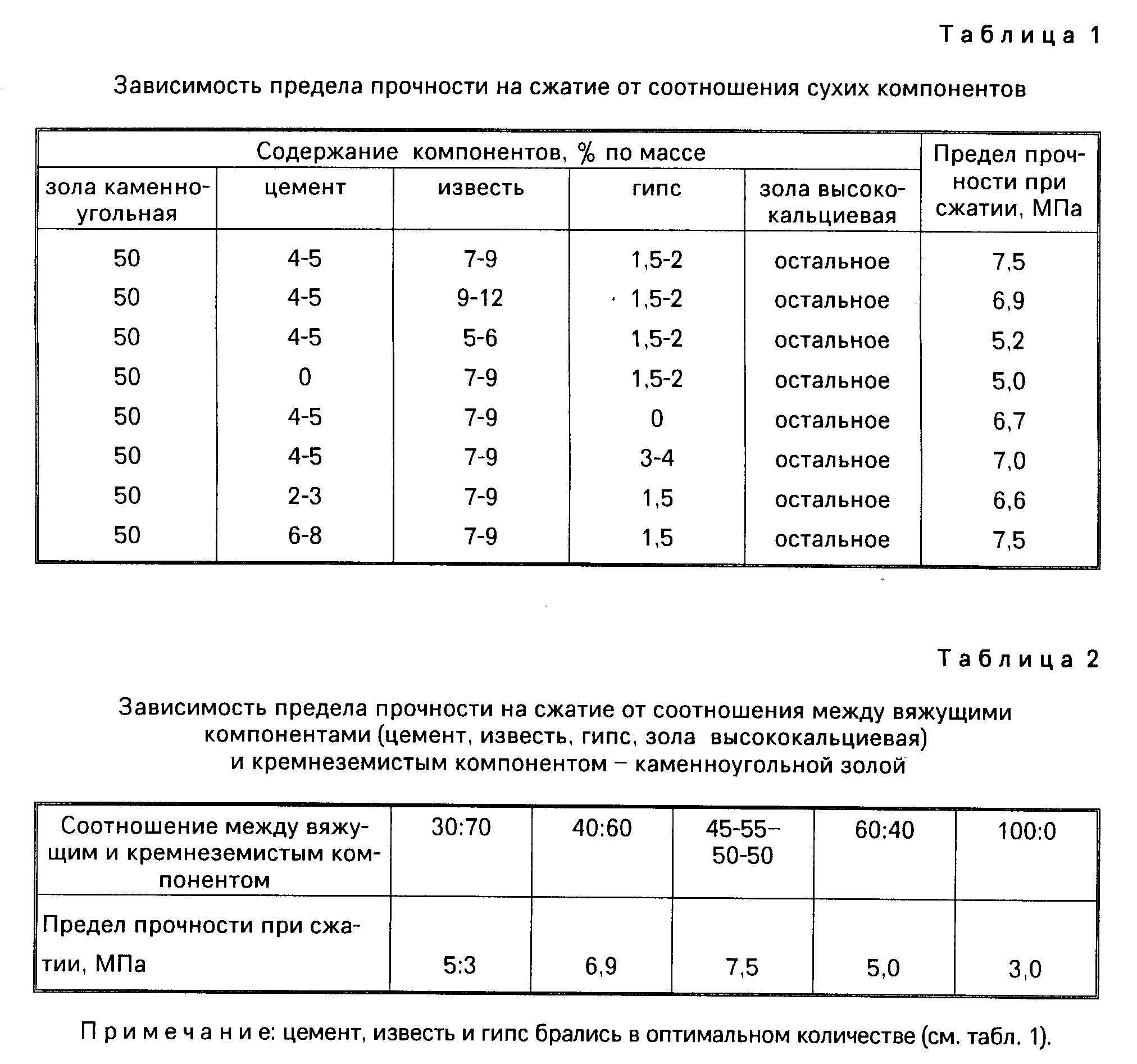
 Для получения подробной информации о том, как вводить данные, см. «Ввод табличных данных», Раздел 3.2.7.
Для получения подробной информации о том, как вводить данные, см. «Ввод табличных данных», Раздел 3.2.7.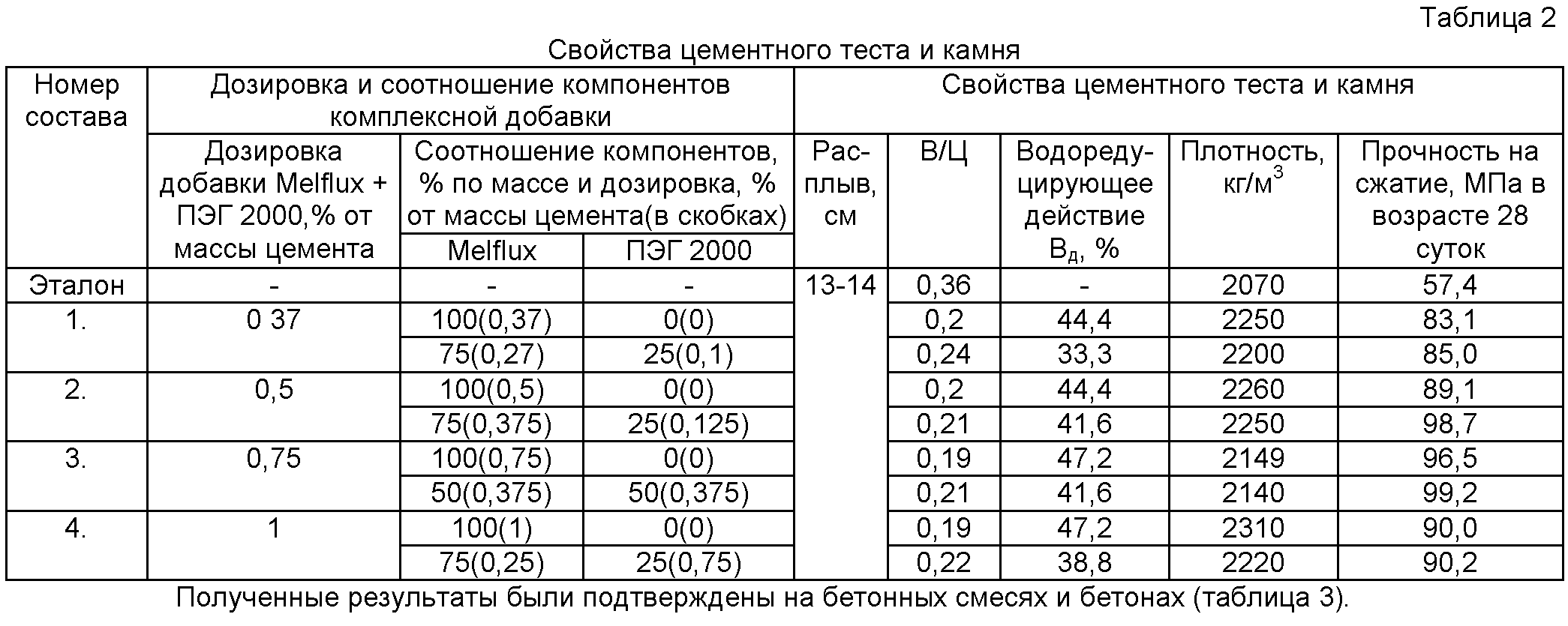 (Безразмерный.) Значение по умолчанию — .
(Безразмерный.) Значение по умолчанию — . (Первое введенное табличное значение всегда должно быть нулевым.)
(Первое введенное табличное значение всегда должно быть нулевым.)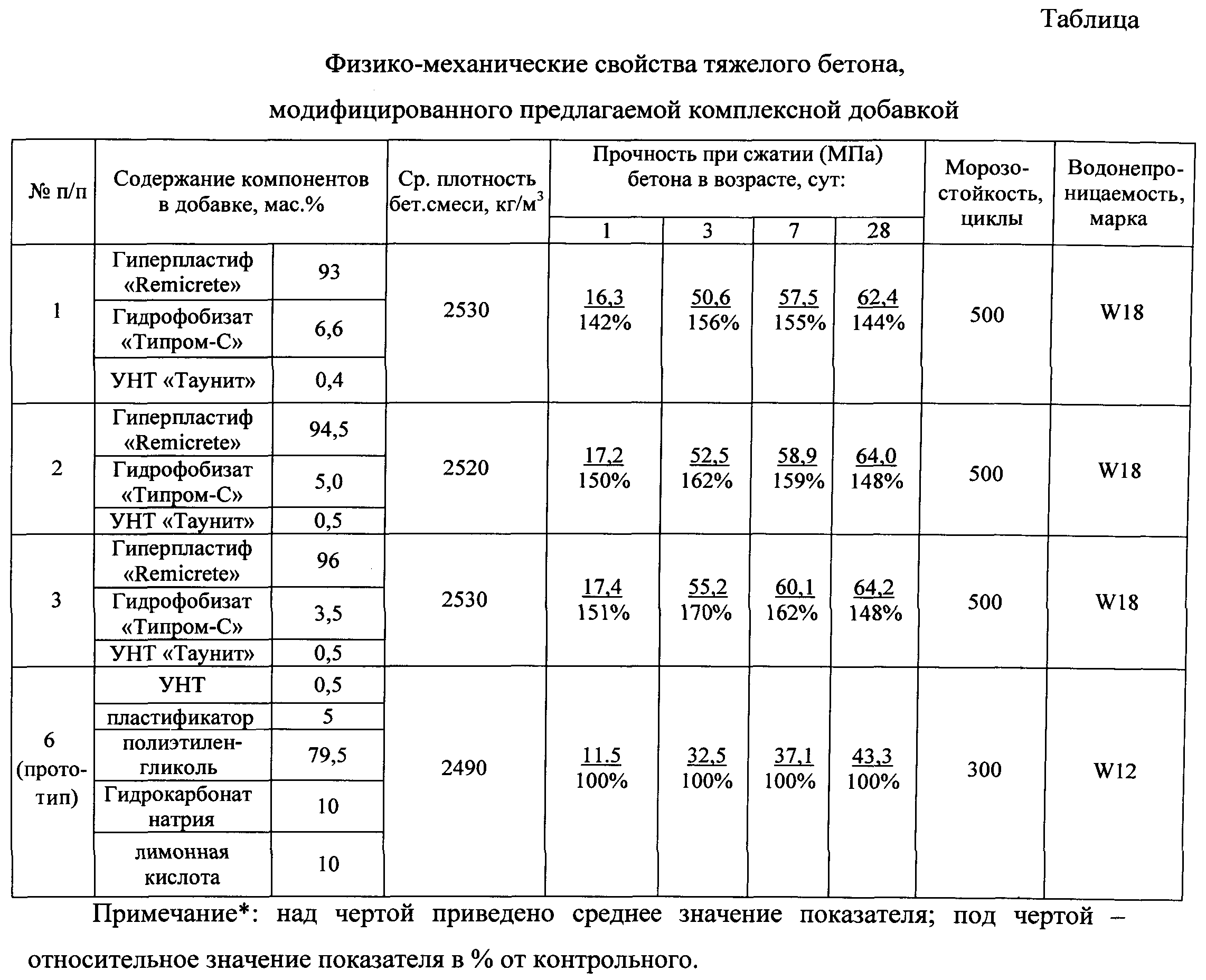
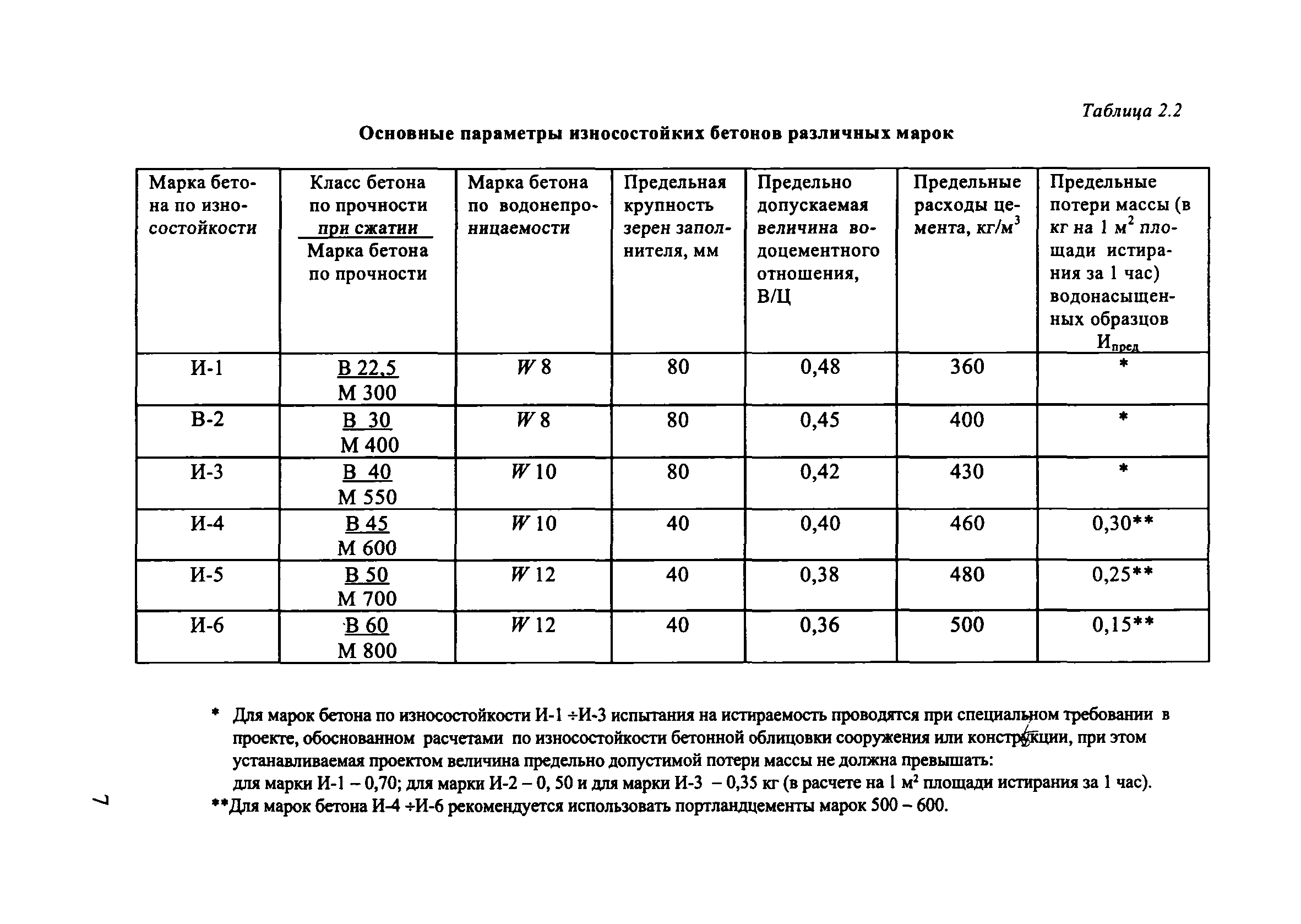
 предполагается 0.
предполагается 0.
 «Просмотр и изменение поведения материала», Раздел 12.7.2, для получения дополнительной информации).
«Просмотр и изменение поведения материала», Раздел 12.7.2, для получения дополнительной информации).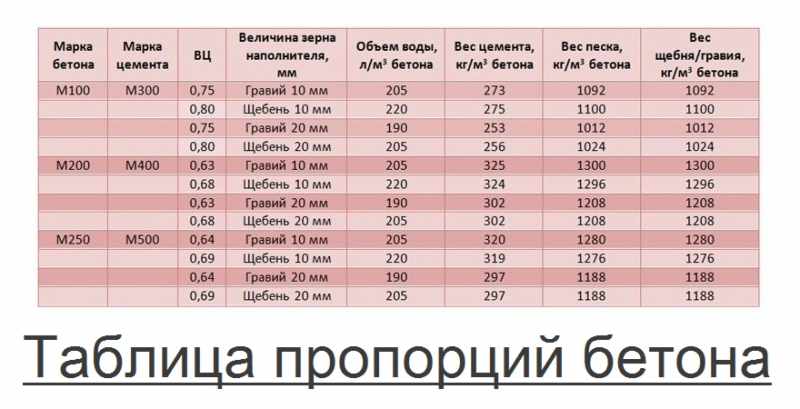
 Значение по умолчанию .
Значение по умолчанию .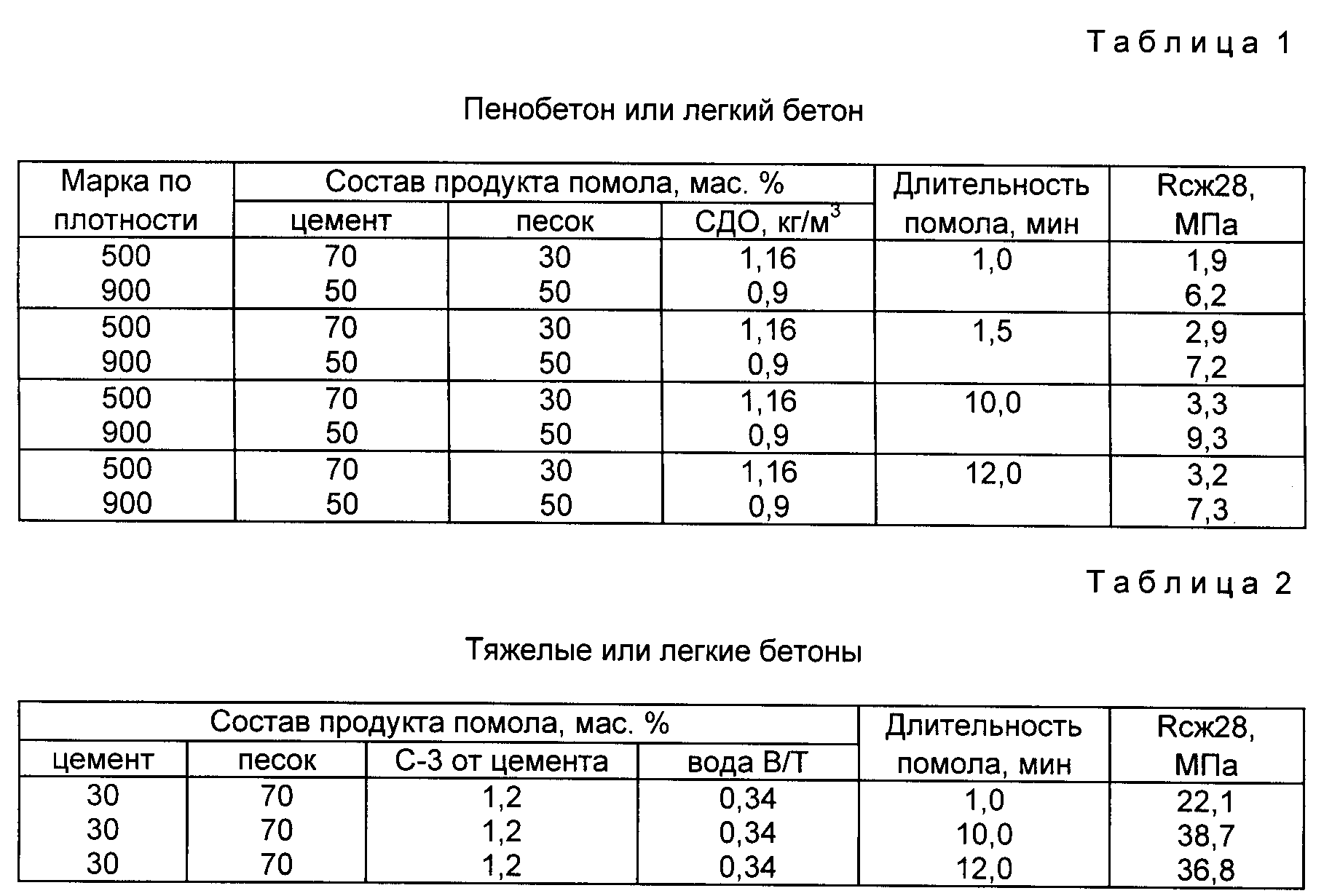
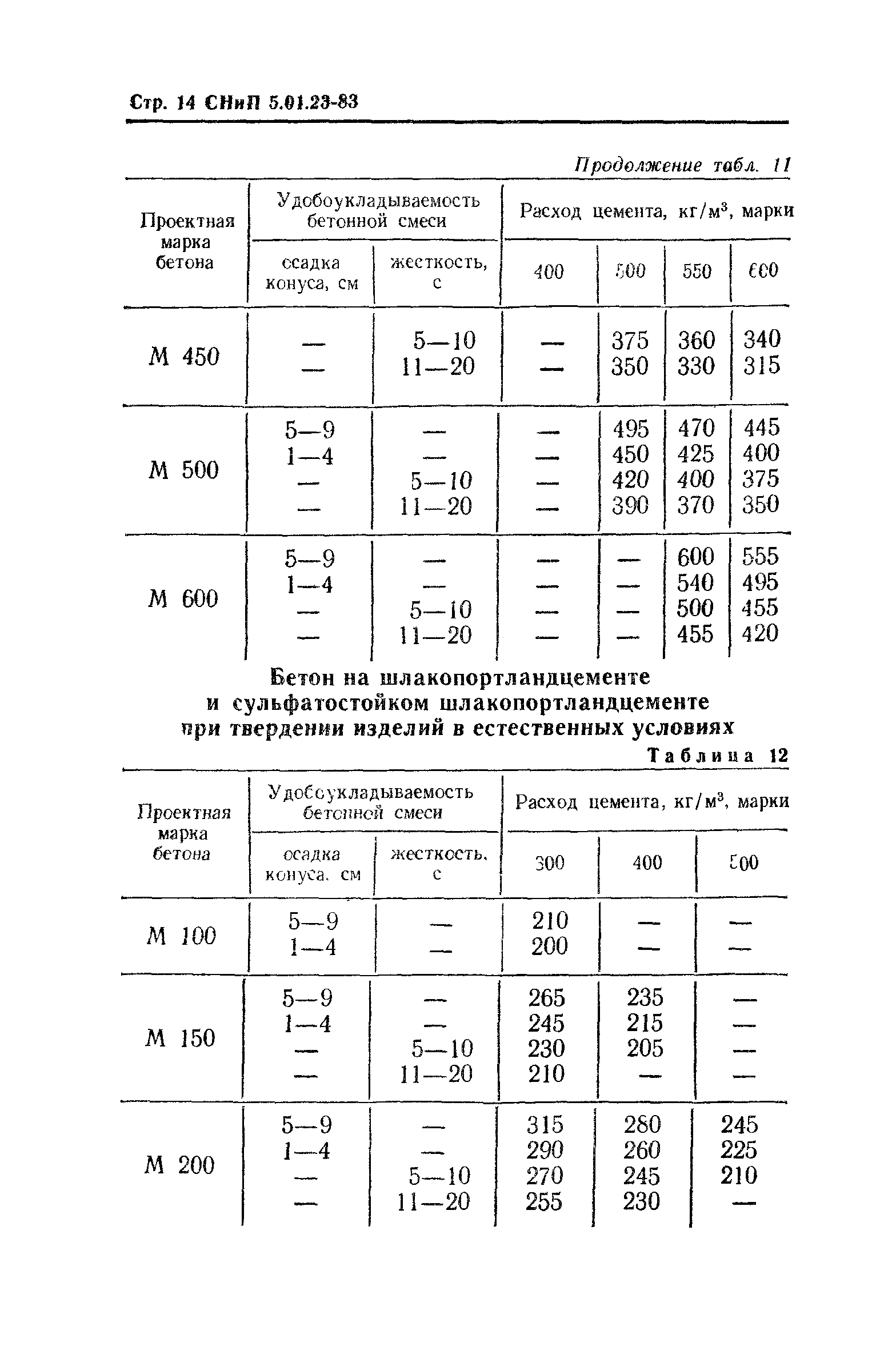 (Информацию о жесткости при растяжении см. в разделе «Определение жесткости при растяжении» в разделе «Пластичность бетона при повреждении», раздел 22.6.3 Руководства пользователя Abaqus Analysis). вход в зависимость послеразрушающее напряжение/растрескивание-деформация.
(Информацию о жесткости при растяжении см. в разделе «Определение жесткости при растяжении» в разделе «Пластичность бетона при повреждении», раздел 22.6.3 Руководства пользователя Abaqus Analysis). вход в зависимость послеразрушающее напряжение/растрескивание-деформация.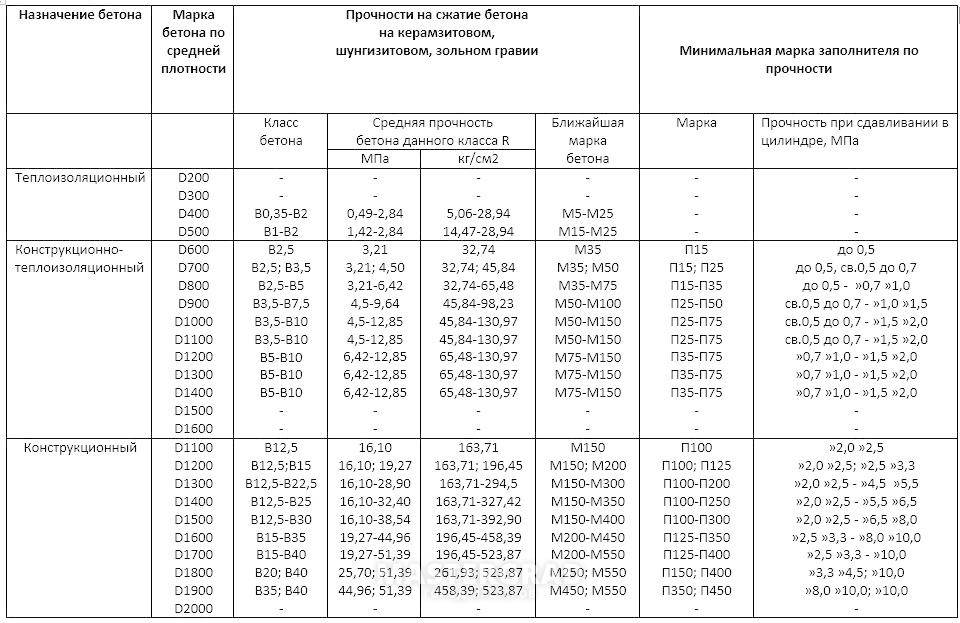
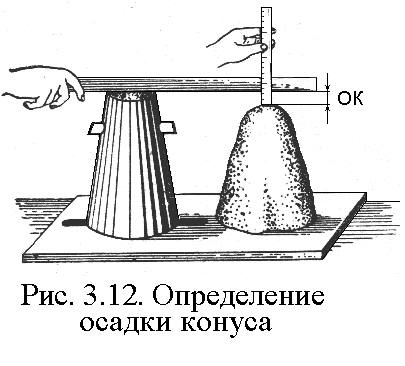 (Единицы .)
(Единицы .)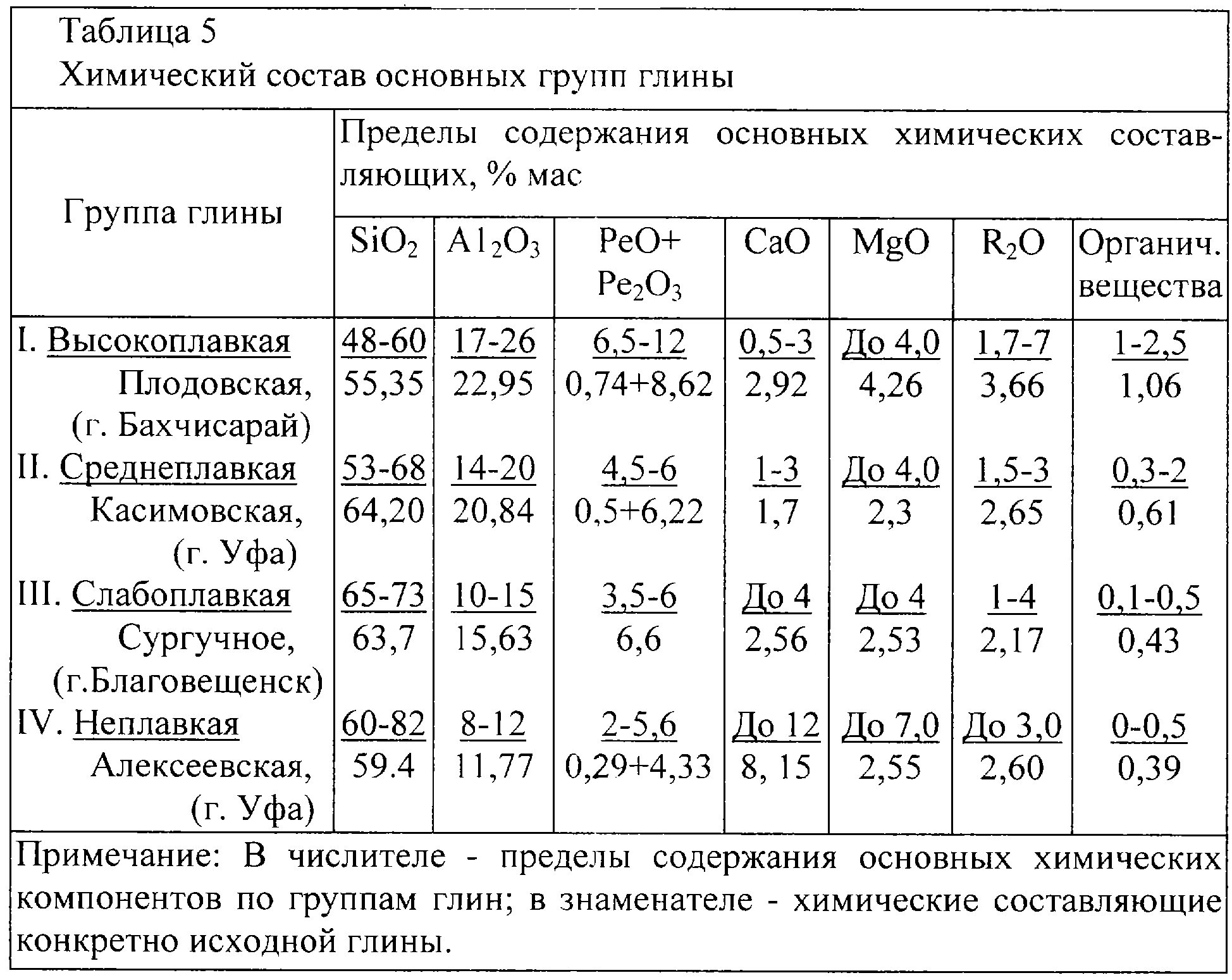
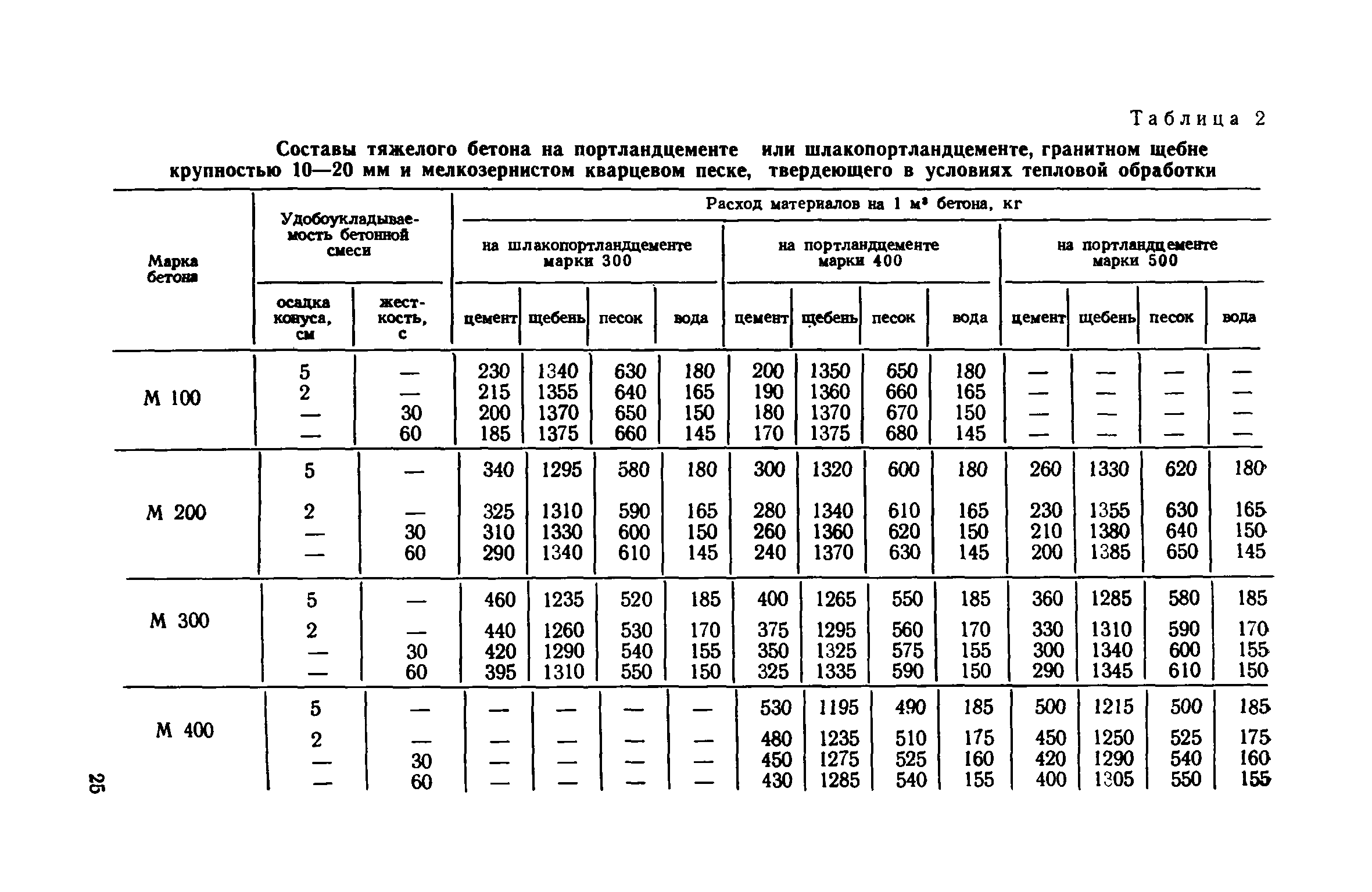 Значение по умолчанию равно , что соответствует допущению о том, что по мере закрытия трещин на жесткость при сжатии не влияет повреждение при растяжении.
Значение по умолчанию равно , что соответствует допущению о том, что по мере закрытия трещин на жесткость при сжатии не влияет повреждение при растяжении.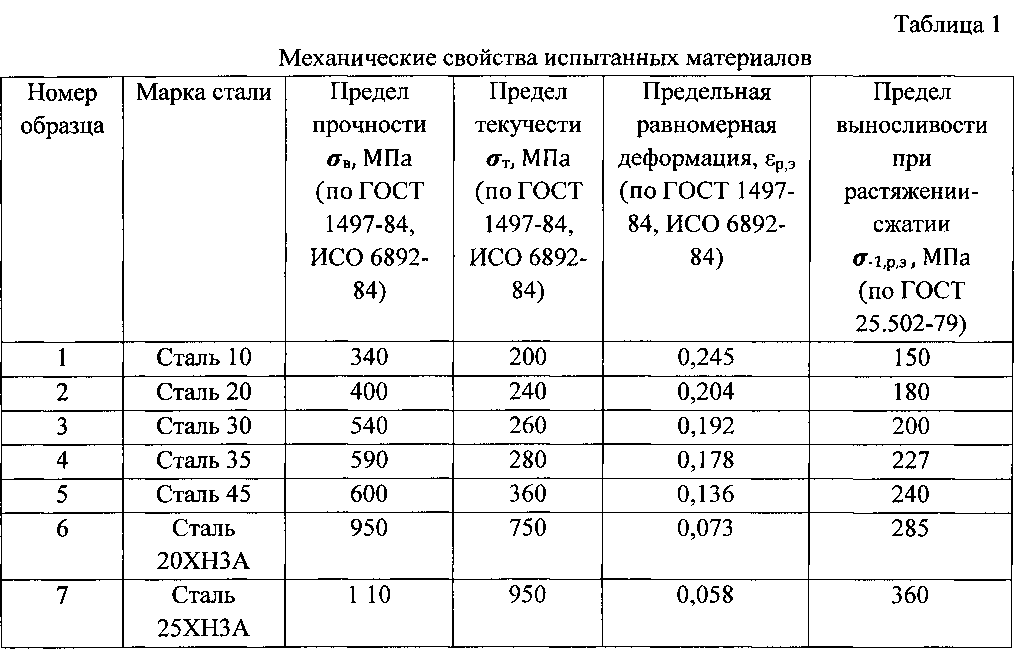
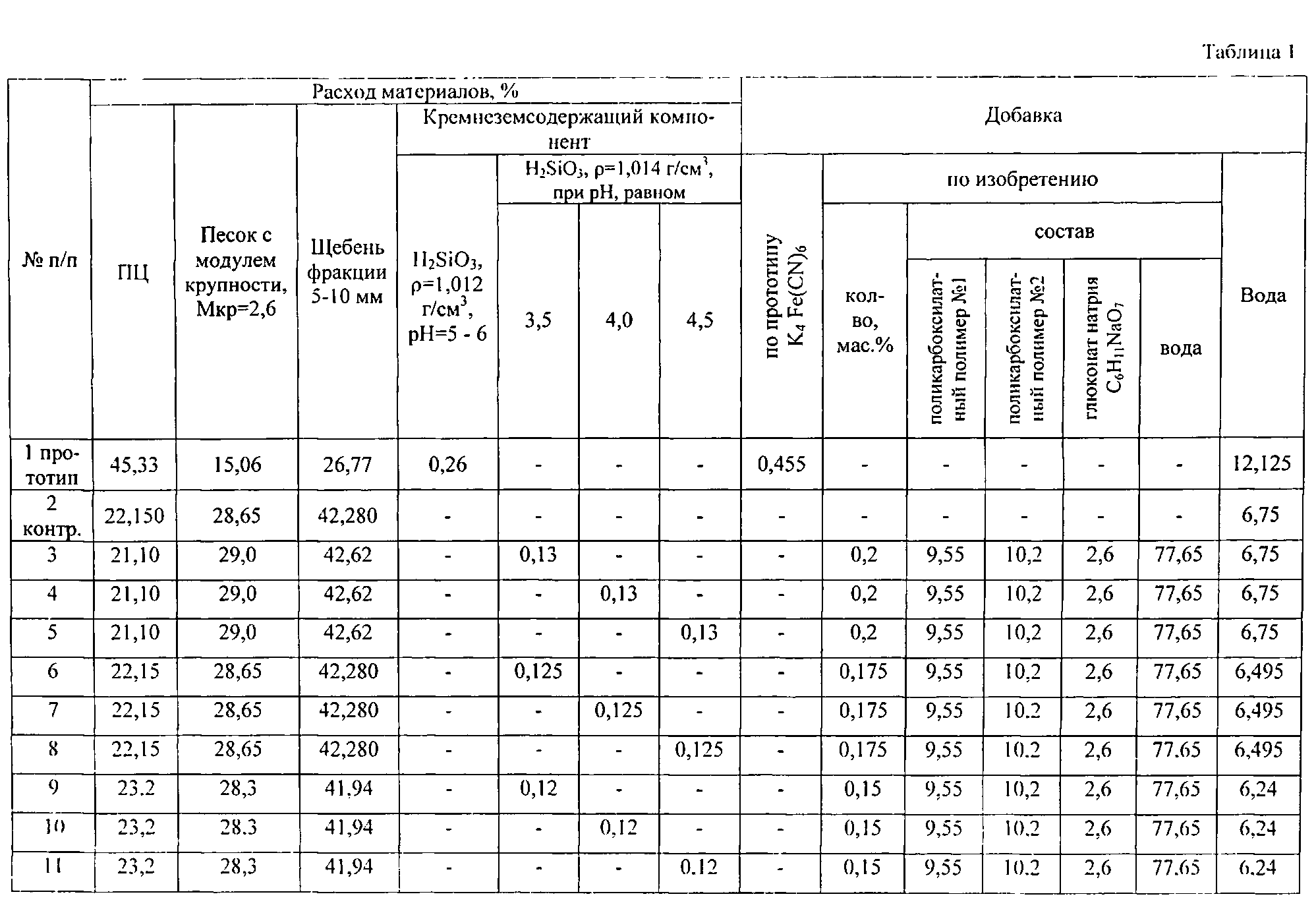
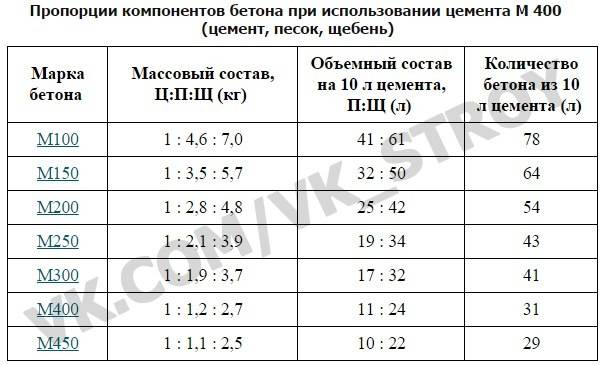
 Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (см. «Просмотр и изменение поведения материала», Раздел 12.7.2, для получения дополнительной информации).
Кроме того, вы можете выбрать другое поведение материала для определения из меню в диалоговом окне Edit Material (см. «Просмотр и изменение поведения материала», Раздел 12.7.2, для получения дополнительной информации). (Единицы л.)
(Единицы л.)
 в разделе «Ввод табличных данных», раздел 3.2.7.
в разделе «Ввод табличных данных», раздел 3.2.7. Эта модель доступна только для анализа Abaqus/Explicit.
Эта модель доступна только для анализа Abaqus/Explicit.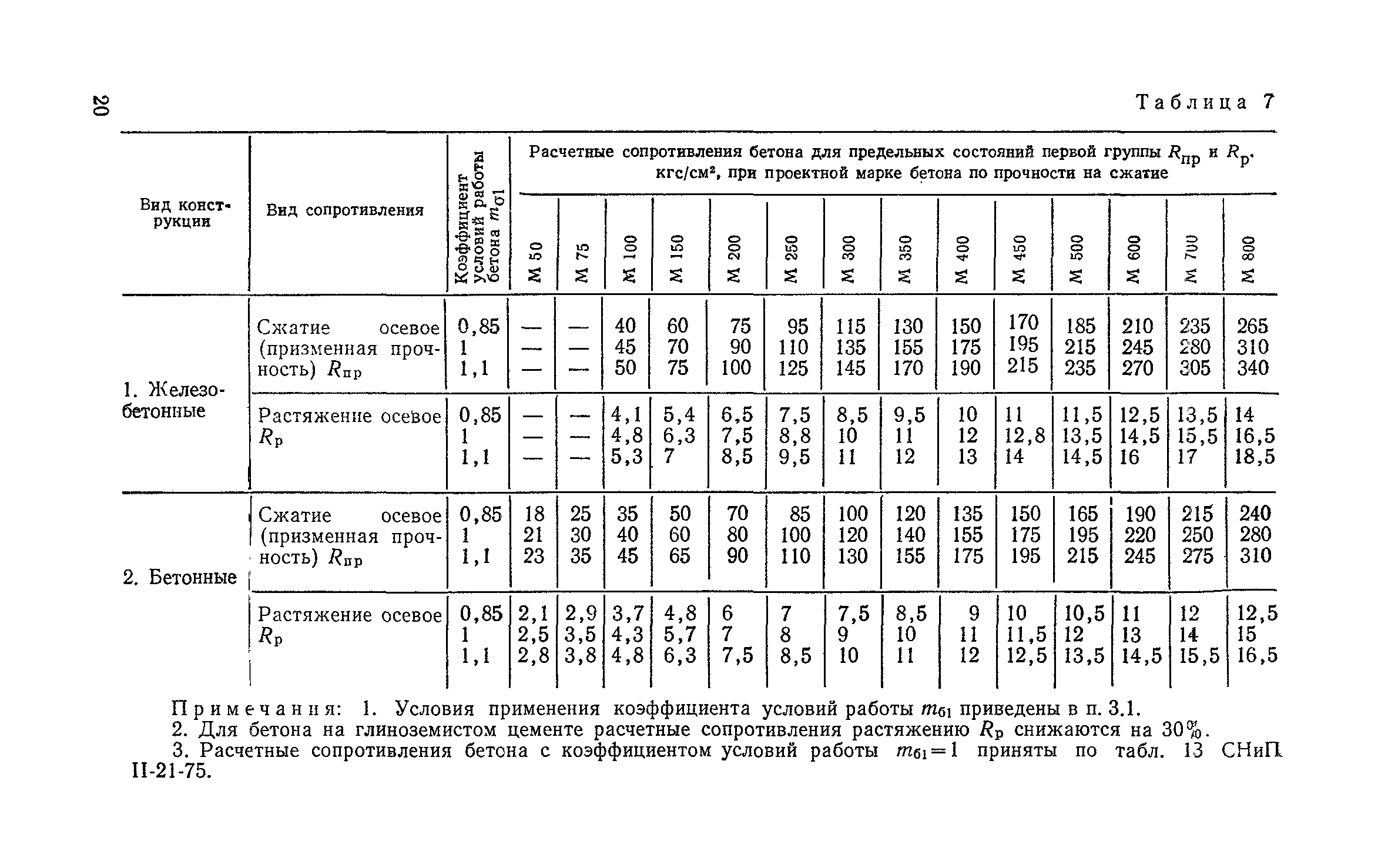 Значение по умолчанию — 1,0.
Значение по умолчанию — 1,0. в разделе «Просмотр и изменение поведения материала», раздел 12.7.2).
в разделе «Просмотр и изменение поведения материала», раздел 12.7.2).

 По умолчанию используется экспоненциальная модель, а если , то для гиперболической модели устанавливается соответствующий поток.Дополнительную информацию см. в разделе «Расширенные модели Друкера-Прагера», раздел 22.3.1 Руководства пользователя Abaqus Analysis.
По умолчанию используется экспоненциальная модель, а если , то для гиперболической модели устанавливается соответствующий поток.Дополнительную информацию см. в разделе «Расширенные модели Друкера-Прагера», раздел 22.3.1 Руководства пользователя Abaqus Analysis.
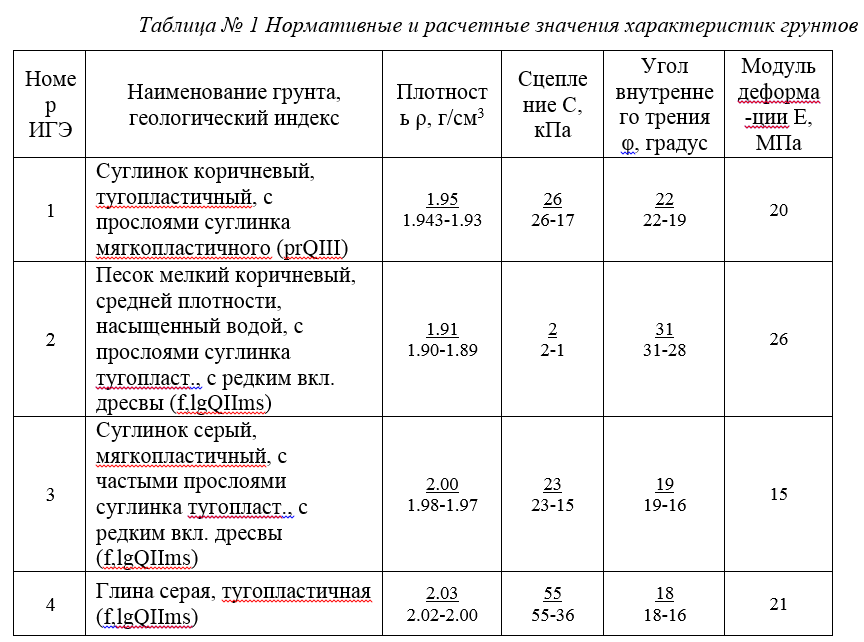
 Подробнее см. в разделе «Определение ползучести Друкера-Прагера».
Подробнее см. в разделе «Определение ползучести Друкера-Прагера».
 (Первое введенное табличное значение всегда должно быть нулевым.)
(Первое введенное табличное значение всегда должно быть нулевым.)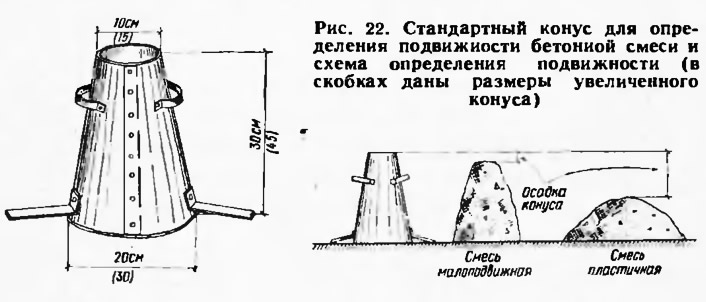
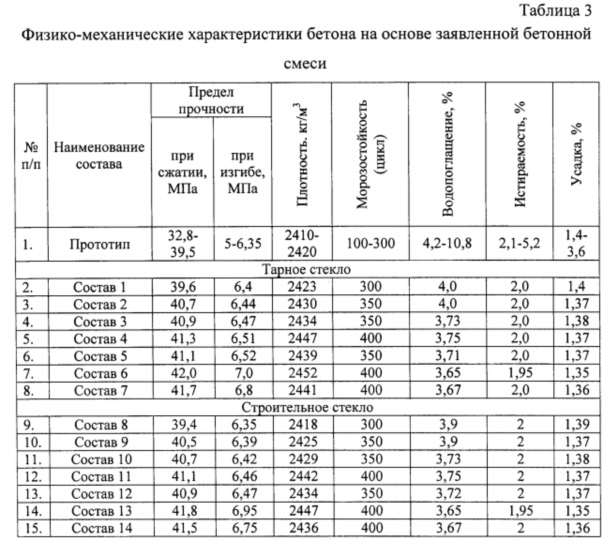

 в разделе «Создание или редактирование материала», Раздел 12.7.1.)
в разделе «Создание или редактирование материала», Раздел 12.7.1.) )
) (Единицы JM 1 1 .)
(Единицы JM 1 1 .) в разделе «Просмотр и изменение поведения материала», раздел 12.7.2).
в разделе «Просмотр и изменение поведения материала», раздел 12.7.2).


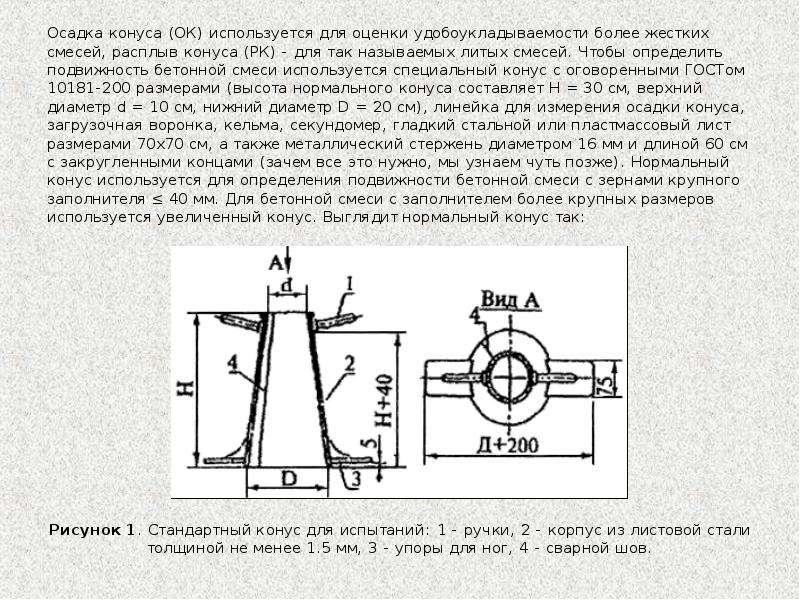
 «Просмотр и изменение поведения материала», Раздел 12.7.2, для получения дополнительной информации).
«Просмотр и изменение поведения материала», Раздел 12.7.2, для получения дополнительной информации). China Railway Design Group Co. Ltd, Тяньцзинь 300143, Китай
China Railway Design Group Co. Ltd, Тяньцзинь 300143, Китай Результаты показали, что критическая высота отслоения как для начального повреждения, так и для полного повреждения постепенно уменьшалась с увеличением длины отслоения.Когда отслоение дошло до второго и третьего анкерных карманов, критические высоты начальных повреждений, вызванных нагрузкой под легковым автомобилем, составили около 0,8 мм и 1,0 мм соответственно; при этом критические высоты под грузовым вагоном составляли около 0,5 мм и 0,8 мм соответственно. Как только высота отслоения превышала критическую высоту начального повреждения из-за развития повреждения плиты пути, общая жесткость конструкции пути на изгиб быстро уменьшалась, что приводило к быстрому увеличению вертикального смещения плиты. конец.Под нагрузкой легкового автомобиля, после того как расслоение дошло до третьего анкерного кармана и высота раскрепления составила более 1,0 мм, раствор СА образовал пустоту, а смещение торца плиты больше не увеличивалось. Под нагрузкой грузового вагона, когда расслоение дошло до третьего анкерного гнезда и высота раскрепления составила более 1,3 мм, вертикальное смещение торца плиты быстро увеличивалось с увеличением высоты раскрепления за счет формирование зоны вторичного повреждения.
Результаты показали, что критическая высота отслоения как для начального повреждения, так и для полного повреждения постепенно уменьшалась с увеличением длины отслоения.Когда отслоение дошло до второго и третьего анкерных карманов, критические высоты начальных повреждений, вызванных нагрузкой под легковым автомобилем, составили около 0,8 мм и 1,0 мм соответственно; при этом критические высоты под грузовым вагоном составляли около 0,5 мм и 0,8 мм соответственно. Как только высота отслоения превышала критическую высоту начального повреждения из-за развития повреждения плиты пути, общая жесткость конструкции пути на изгиб быстро уменьшалась, что приводило к быстрому увеличению вертикального смещения плиты. конец.Под нагрузкой легкового автомобиля, после того как расслоение дошло до третьего анкерного кармана и высота раскрепления составила более 1,0 мм, раствор СА образовал пустоту, а смещение торца плиты больше не увеличивалось. Под нагрузкой грузового вагона, когда расслоение дошло до третьего анкерного гнезда и высота раскрепления составила более 1,3 мм, вертикальное смещение торца плиты быстро увеличивалось с увеличением высоты раскрепления за счет формирование зоны вторичного повреждения.

 3969/j.issn.1001-8360.2019.03.015
3969/j.issn.1001-8360.2019.03.015 工程力学, 2015, (6): 124- 132
工程力学, 2015, (6): 124- 132  Journal of Engineering Mechanics, 1998, 124 (8): 892- 900
Journal of Engineering Mechanics, 1998, 124 (8): 892- 900  Railway Standard Design, 2013, (12): 50- 53
Railway Standard Design, 2013, (12): 50- 53 中国铁道科学, 2012, 33 (1): 6- 12
中国铁道科学, 2012, 33 (1): 6- 12  基于连续损伤力学的混凝土疲劳损伤模型[D]. 哈尔滨: 哈尔滨工业大学, 2009.
基于连续损伤力学的混凝土疲劳损伤模型[D]. 哈尔滨: 哈尔滨工业大学, 2009.  混凝土结构设计规范: GB 50010−2010[S]. 北京: 中国建筑工业出版社, 2014: 211.
混凝土结构设计规范: GB 50010−2010[S]. 北京: 中国建筑工业出版社, 2014: 211. 预应力钢棒失效对CRTS Ⅰ 型单元轨道板受力性能的影响[D]. 成都: 西南交通大学, 2014.
预应力钢棒失效对CRTS Ⅰ 型单元轨道板受力性能的影响[D]. 成都: 西南交通大学, 2014.