Размер ступеньки: Размер ступенек по госту
Размер ступенек по госту
Лестница – важная деталь любого дома. Ключевым ее элементом является ступенька. От того, какой размер вы выберете, будет зависеть не только внешний вид конструкции, но и удобство ее использования. Давайте подробно разберемся в том, какая высота и ширина ступени считаются оптимальными, и как их правильно рассчитать.
Размер ступеней по ГОСТу и СНИПу
Размер, согласно ГОСТу и СНИПу, определяется, исходя из следующих параметров:
- общий угол наклона лестницы;
- высота ступени;
- ширина лестничного марша.
При этом используются следующие нормативные документы:
- ГОСТ 8717.1-84 – устанавливает необходимые нормы для размеров различных элементов лестниц.
- ГОСТ 23120-78 – определяет требования, предъявляемые к конструкциям, относящимся к маршевым трапам.
Исходя из их содержания, можно выделить следующие габариты, соответствующие общепринятым нормам:
- высота ступени, согласно ГОСТу, должна составлять не менее 12 и не более 25 сантиметров;
- минимальная ширина должна варьироваться в пределах 70-80 сантиметров;
- оптимальной считается конструкция, ширина которой составляет 1 метр;
- ширина ступени лестницы, согласно норме, должна составлять 27-30 сантиметров.
 Это необходимо для того, чтобы человек мог опереться на конструкцию всей подошвой, и она не свисала с края.
Это необходимо для того, чтобы человек мог опереться на конструкцию всей подошвой, и она не свисала с края.
Обратите внимание! В некоторых случаях, например, при проектировании лестницы на чердак допускается возведение конструкций шириной 60 сантиметров.
В данном видео вы узнаете, какая должна быть высота ступени:
Согласно СНИП, можно выделить следующие показатели:
- Высота стандартной ступени лестницы должна составлять не более 15 сантиметров.
- Погрешность, допускаемая в размерах ступеней одного лестничного марша, не должна превышать 5 миллиметров.
- Их число не должно быть меньше 3 и не больше 18.
- Желательно, чтобы количество определялось нечетным числом. Это позволит начинать движение по лестнице и заканчивать его с одной ноги, что очень удобно.
- Наклон лестницы считается комфортным, если его значения лежат в интервале от 35 до 40 градусов.
- Ширина ступеньки – не менее 30 сантиметров.

Подробнее о нормах СНИП можно узнать из документов:
- № 2.08.02/89 – правила постройки общественных зданий;
- № 2.08.01/89 – правила постройки жилых помещений.
Некоторые значения могут изменяться в большую или меньшую сторону, в зависимости от того, где будет располагаться конструкция.
Оптимальный и удобный размер ступеней лестницы в доме
Итак, мы разобрались с шириной и высотой ступени, которые считаются оптимальными, согласно СНИПу и ГОСТу. Теперь давайте попытаемся разобраться, как получить наиболее оптимальный и удобный размер конструкции.
Сразу хочется отметить тот факт, что расчет ступеней и общего размера лестницы зачастую зависит от способа ее применения и габаритов помещения. Проектирование чердачных и подвальных конструкций может отличаться от межкомнатных. Исходя из этого, можно сделать вывод, что проектирование по ГОСТу не всегда может оказаться верным решением.
Существует ряд правил, придерживаясь которых, вы сможете определить оптимальный и удобный размер лестницы и ее элементов:
- Угол подъема не должен превышать отметку в 40 градусов.

- Проектируйте глубину проступи таким образом, чтобы нога самого большого члена вашей семьи опиралась на поверхность подступенка всей подошвой. Это значительно повысит безопасность подъема.
- Старайтесь рассчитать размер ступеней таким образом, чтобы их количество было равно 15. Такая лестница будет максимально удобной для подъема.
Отдельно хочется отметить тот факт, что угол наклона может значительно изменить размер конструкции для того, чтобы она оставалась комфортной и безопасной. Так, например:
- при угле наклона в 30° ширину проступи необходимо делать равной 30 см, а ее высоту – 15 см;
- если угол доходит до отметки в 40°, необходимо скорректировать размеры. Ширина станет равна 25 сантиметрам, а высота корректируется до отметки в 20 сантиметров.
Это необходимо для того, чтобы увеличить безопасность спуска и подъема. При строительстве крутых лестниц не забудьте построить удобные и надежные перила.
Способы расчета ступеней лестничного марша
Для того чтобы рассчитать количество ступеней лестничного марша, можно воспользоваться одним из следующих способов:
- использовать графический метод;
- разделить расстояние между этажами на желаемую высоту проступи;
- воспользоваться специальным калькулятором на нашем сайте.

Использование графического метода позволит вам получить необходимые параметры конструкции, беря за основу угол ее наклона и количество ступеней. Для реализации этого метода необходимо придерживаться следующего алгоритма:
- Чертим ось координат.
- Одну ось разбиваем на отрезки, равные длине шага, а вторую – на отрезки, равные его высоте.
- Соединяем синими линиями получившуюся разбивку.
- Фиолетовой линией обозначаем угол наклона.
- На пересечении чертим пунктиром две линии, которые будут параллельны нашим осям.
- Таким образом, у нас получается готовый контур, который, для удобства, можно обвести красным цветом.
- При необходимости можно внести корректировки в размер конструкции, с учетом поправок на масштаб.
При разделении расстояния между этажами на высоту проступи у нас возникнет проблема, связанная с тем, что полученное число может оказаться дробным. Устранить ее удастся следующими способами:
- Сделать нижнюю ступеньку нестандартной по высоте, изменив ее на необходимую величину.
 Ее размер будет равен произведению полученного остатка на исходную высоту.
Ее размер будет равен произведению полученного остатка на исходную высоту. - Равномерно распределить полученный остаток на все ступени. Для этого нам нужно умножить полученный остаток на число ступеней. Полученное значение добавляется к целому числу. Таким образом, мы получим минимальное изменение в размерах.
Использование калькулятора для расчета количества ступеней – самый простой способ получить нужную информацию. Этот инструмент позволяет рассчитывать количество ступеней для разных конфигураций лестниц, с учетом различных факторов.
Необходимые формулы для расчета
Если вы желаете рассчитать все самостоятельно, воспользуйтесь следующими формулами:
- формула безопасности. Количество рассчитывается на основании следующего соотношения – суммы глубины проступи и высоты подступенка должны быть равны 46 сантиметрам;
- формула Блонделя. За основу берется средний шаг человека. Формула выглядит следующим образом: 2h + B = 600…640 миллиметров, где
- H – высота проступи;
- В – ширина проступи;
- 600…640 – средняя длина человеческого шага.

Проектирование лестницы осуществляется по определенным стандартам, которые регламентированы такими документами, как СНиП и ГОСТ. Установленные стандарты обеспечивают удобство и безопасность сооружения для комнаты или для крыльца.
Среди прочего, ГОСТ определяет их конструктивные особенности, параметры и технические условия изготовления. СНиП окажет помощь тем, кто самостоятельно обустраивает лестничный марш. Там содержатся подробности, касающиеся расчетов (высота подступенка, ширина марша и прочее) и проектирования.
Параметры ступеней внутренних лестничных маршей
Для того, чтобы подниматься и спускаться было комфортно, должны выдерживаться оптимальные размеры. Ниже представлены ключевые параметры лестничных ступеней (в миллиметрах):
- ширина ступени — от 200 до 320;
- высота ступени — от 150 до 200;
- максимальный выступ ступени – 30;
- предельно допустимая разница между подступенками одного пролета – 5.

Важно правильно определить ширину проступи. Соотношение габаритов ступени выражается разными формулами. Первая называется «формулой удобства»: между размерами проступи и подступенка разница составляет 120. Вторую обозначают как «формулу безопасности»: сумма размеров проступи и подступенка равна 450. Эти вспомогательные уравнения помогут найти оптимальный баланс параметров ступени.
Требования ГОСТ, в которых оговаривается ширина деревянных и других ступеней, рассчитаны для удобного спуска и подъема. Считается, что наиболее комфортной является высота подступенка 150 мм при вдвое большей (то есть равной 300) ширине проступи. Увеличение последнего показателя приведет к тому, что для подъема на один уровень придется делать несколько шагов. Если ширина ступени будет уменьшена, спуск будет неудобным.
Требования ГОСТ, касающиеся безопасности, нужно соблюдать как при строительстве, так и при эксплуатации лестничного марша.
Строительные нормативы затрагивают все лестничные конструкции.
Параметры площадок и ограждений
Чтобы лестничные площадки были удобными, они также должны быть спроектированы в соответствии со стандартами. Их полезная ширина не должна быть меньше ширины марша, прилегающего к ней. Для комфортного перемещения оптимальная длина площадки должна быть не менее 1300 мм. Если поблизости расположена дверь, при проектировании необходимо сделать размер площадки с учетом размера дверного полотна.
Для безопасности лестницы предусмотрены ограждения. Высота перил не должна быть меньше 900 мм, для ограждений крыльца (при количестве ступеней более трех) минимальный показатель – 800. В целях безопасности детей высота ограждения может быть увеличена до 1500.
Параметры ступени на путях эвакуации
Что касается пунктов о путях эвакуации, глубина проступи и высота подступенка четко регламентированы – 250 и 220 мм соответственно. На путях эвакуации требуется наличие выхода на прилегающую территорию – либо прямого, либо через вестибюль. Для последнего обязательно наличие светового проема площадью минимум 1,2 м2.
На путях эвакуации требуется наличие выхода на прилегающую территорию – либо прямого, либо через вестибюль. Для последнего обязательно наличие светового проема площадью минимум 1,2 м2.
| Видео (кликните для воспроизведения). |
Важно:
На путях эвакуации все лестницы (в том числе и пожарные лестницы для работы бригад спасателей) производятся из негорючих материалов. Запрещено наличие деревянных элементов.
[1]
Конструирование лестницы для крыльца
Для деревянных ступеней для крыльца применимы те же параметры, что и для внутренних ступеней. Однако есть некоторые нюансы. Угол наклона лестницы для крыльца не должен превышать 30º, чтобы по ней было удобно подниматься. Габариты ступени крыльца находятся в тех же пределах – высота в среднем 140-170 мм, глубина – не менее 250.
Широко распространено обустройство для крыльца деревянных ступеней. Однако чтобы продлить срок их службы, дерево пропитывают защитными составами. Предпочтительно использование для крыльца твердых пород древесины.
Предпочтительно использование для крыльца твердых пород древесины.
Проектирование и возведение лестницы требует немалых затрат. Но при соблюдении строительных нормативов вполне возможно качественно выполнить эту работу. Оставьте комментарий и поделитесь полезными советами по проектированию лестницы.
(0 голосов, среднее: 0 из 5)
Лестницы – важнейший элемент зданий. Подходить к проектированию этого элемента стоит очень тщательно. Существуют нормы, касающиеся всех параметров марша, которые необходимо соблюдать в обязательном порядке. Высота перил, ширина пролёта, количество проступей в марше – всё важно.
Установленные параметры и требования СНиП к ступеням
Размер имеет значение!
Стандартные и другие проступи
Ступеньки являются одной из основных важных функциональных частей лестничной конструкции. От их конфигурации напрямую зависит удобство и безопасность конструкции. При их проектировании должны учитываться точно выверенные размеры, расчёт которых производился с давних времён.
Изыскания в области абсолютной безопасности и удобства лестниц велись издавна Ещё в семнадцатом веке во Франции один из ведущих инженеров-конструкторов рассчитал формулу, по которой вычислялись необходимые параметры для ступени и подступенка.
Выглядела эта формула таким образом: 2x+y=60, где x – высота между горизонтальными поверхностями проступей, а y – ширина проступи, расстояние между двумя ближайшими вертикальными поверхностями.
[2]
Позже с тех времён и до нашего времени были выведены и другие формулы, и среди них две самые известные: x+y=45 и y-x=12. Первая отвечает требованиям безопасности, а вторая — удобства.
Современные стандарты
В наше время нормы и правила приобрели более завершённый вид и досконально отражены перечне СНиП. Параметры, которые имеют значение при конструировании лестничных ступеней:
- ширина;
- длина;
- высота;
- соотношение высоты и ширины;
- различие разных ступеней по размерам в пределах одного марша;
- количество проступей.

Требования по СНиП
В строительных нормах и правилах все требования к ступеням, как и к лестницам в целом, подробно описаны и полностью регламентированы. Нарушение этих норм при строительстве государственных объектов строго наказуемо и ведёт к штрафам.
Другие правила, рекомендуемые к исполнению
Количество ступенек в одном марше должно быть от трёх до семнадцати. В более ранних документах существовал допуск восемнадцати проступей, но потом для большего удобства решили делать нечётное количество. Также настоятельно не рекомендуется делать ступеньки одного марша с перепадом высоты более пяти миллиметров. В случае если ее значение различается, человек испытывает трудности при спуске-подъёме.
Если вы будете при строительстве соблюдать все перечисленные правила и произведете правильный расчет лестничного марша, он будет удобным, безопасным и комфортным для передвижения.[3]
При расчёте по несущей способности элементы лестницы расчленяются на статически определимые балки — консольные или однопролётные, и рассчитываются по соответствующим формулам. Так как лестницы подвержены действию динамических нагрузок, к жёсткости несущих элементов предъявляются повышенные требования: прогиб их не должен превышать 1/400 пролёта. Нагрузки, действующие на лестничные марши и площадки, должны собираться путем сложения собственного веса конструкций и временных нагрузок: в жилых домах — 300 кг/м².
Так как лестницы подвержены действию динамических нагрузок, к жёсткости несущих элементов предъявляются повышенные требования: прогиб их не должен превышать 1/400 пролёта. Нагрузки, действующие на лестничные марши и площадки, должны собираться путем сложения собственного веса конструкций и временных нагрузок: в жилых домах — 300 кг/м².
При подъеме человек затрачивает примерно в два раза больше энергии, чем при движении по горизонтали (рис. 2). Практикой установлено: лестница удобна и безопасна, если удвоенная высота подступёнка, сложенная с шириной ступени (проступью), равняется среднему шагу человека. Длина шага человека на плоскости составляет примерно 600–640 мм. Исходя из этого, проступь и подъем определяют по формуле: 2а+b = 600…640 мм.
рис.2. Расчет высоты и ширины рядовых ступеней
Как альтернативу можно использовать другую, более легкую для запоминания, формулу: а+b = 450 ± 20 мм, где а — высота ступени (подступёнка), b — ширина ступени (проступи).
Ширина проступи должна обеспечивать опирание ноги полной стопой, то есть быть не меньше 200 и не больше 320 мм. Оптимальной считается высота подступёнка, равная 150, а ширина проступи — 300 мм. При сильном увеличении ширины проступи вы непременно собьетесь с шага, а при сильном уменьшении затруднится спуск. При проектировании забежных ступеней нужно учитывать, что минимальная ширина ступеней с узкого конца должна составлять не менее 100 мм, а нависание проступи над нижней ступенькой должно быть не более 50 мм. Так же нависание верхней ступени над нижней делается тогда, когда другими способами не удается увеличить ширину проступи, в этом случае величина нависания не должна превышать 30 мм для деревянных и 50 мм для железобетонных ступеней.
Оптимальной считается высота подступёнка, равная 150, а ширина проступи — 300 мм. При сильном увеличении ширины проступи вы непременно собьетесь с шага, а при сильном уменьшении затруднится спуск. При проектировании забежных ступеней нужно учитывать, что минимальная ширина ступеней с узкого конца должна составлять не менее 100 мм, а нависание проступи над нижней ступенькой должно быть не более 50 мм. Так же нависание верхней ступени над нижней делается тогда, когда другими способами не удается увеличить ширину проступи, в этом случае величина нависания не должна превышать 30 мм для деревянных и 50 мм для железобетонных ступеней.
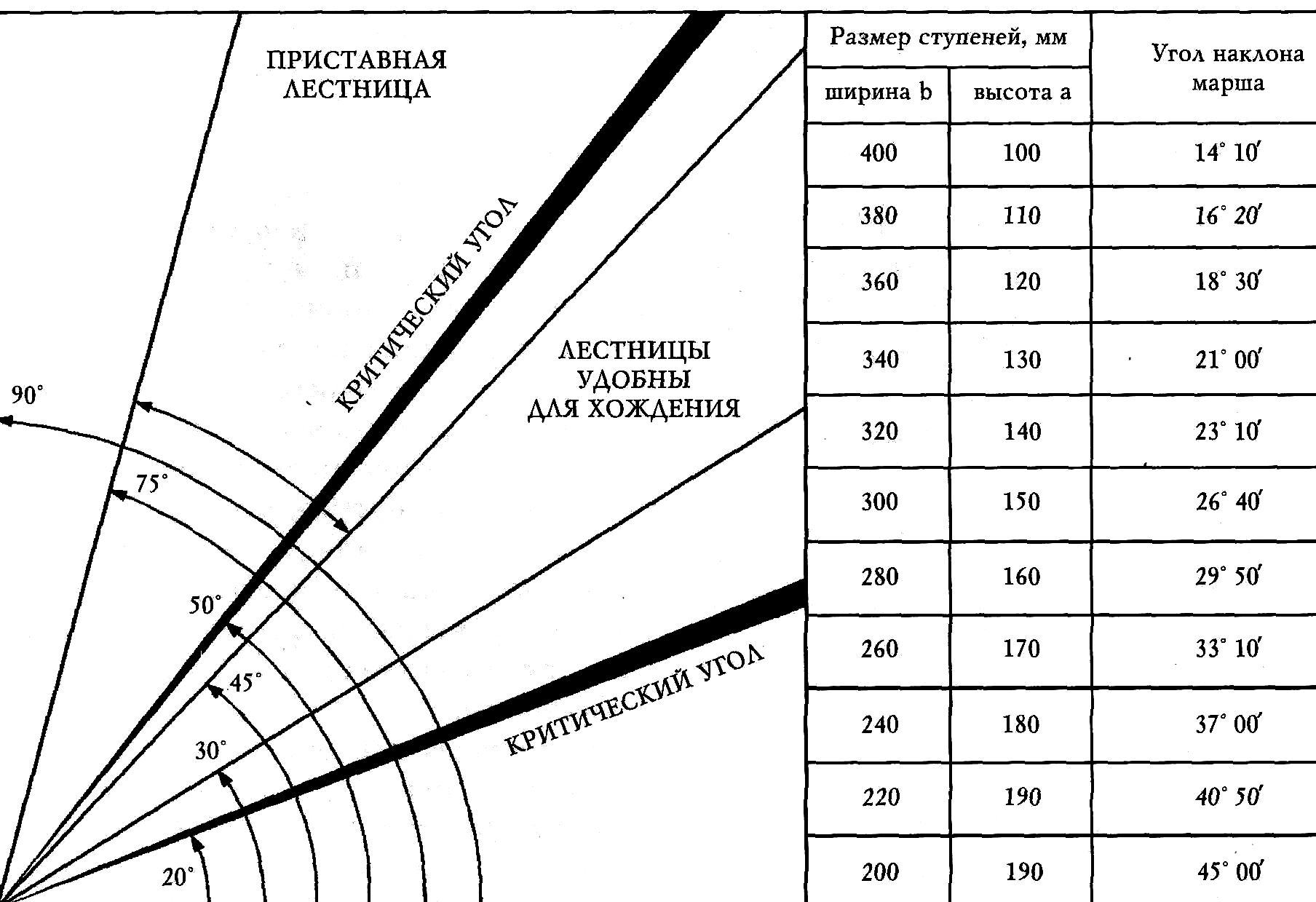
Наиболее удобные углы подъёма лестницы находятся в диапазоне от 23 до 37°. Чем лестница круче, тем меньше ей надо места для установки в доме, и соответственно, чем лестница положе, тем больше места необходимо для неё предусмотреть. Если угол меньше 23° — лестницу можно заменить пандусом (ровной наклонной площадкой), если больше 45°, то лестница переходит в разряд приставных или раскладных (рис. 3). Оптимальный угол подъема винтовых лестниц — 25–35°. Наиболее сложным процессом при крутизне лестничного марша более 40° является спуск с лестницы, а при углах более 45° спуск можно осуществлять только спиной вперед.
3). Оптимальный угол подъема винтовых лестниц — 25–35°. Наиболее сложным процессом при крутизне лестничного марша более 40° является спуск с лестницы, а при углах более 45° спуск можно осуществлять только спиной вперед.
рис. 3. Нормативная зависимость размеров ступеней от крутизны лестницы
Количество ступеней зависит от высоты этажа и угла наклона лестницы. Зная местоположение лестницы в плане и высоту помещения, количество ступеней можно (и проще) установить графически, а после этого, по формулам безопасности определить ширину проступи.
Для графического построения лестницы на миллиметровой бумаге или бумаге «в клеточку» нужно в масштабе нарисовать лестничный марш (рис. 4) соизмеряя его с высотой этажа.
рис. 4. Пример графического расчета количества ступеней и высоты подступёнка. Таблица высот для ступенек в зданиях с нормативной высотой этажа
Высотой этажа называется разница высотных отметок уровней чистого пола нижнего и верхнего этажа, то есть в размер высоты этажа должны быть включены толщины одежды полов. Например, пол нижнего этажа облицован керамической плиткой, а пол верхнего этажа выложен паркетом по лагам и фанерному «черному полу». В расчет высоты этажа должны быть включены все слои данных половых конструкций: внизу — толщины выравнивающей стяжки, плиточного клея и плитки; вверху — толщина лаг, фанеры и паркета. В России еще со времен существования СССР высота этажа — величина регламентированная. Обычно стандартная высота этажа равна 2,8 или 3 м, реже — 2,7 или 3,3 м, что позволяет проектировать высоту помещения (расстояние от пола до потолка) не менее 2,4 м. Такая высота этажа позволяют без особого труда вписать лестницу с размерами ступеней, отвечающим требованиям расчетной формулы безопасности (рис. 4, таблица 2). Если ваша высота этажа отличается от нормативной и не кратна 3, то высоту ступеней нужно рассчитывать (округлять) с точностью до одного миллиметра, но так, чтобы высоты всех подступёнков были одинаковыми. Погрешность вычисления, набегающую от округления высот, лучше распределить на нижнюю фризовую ступень, а остальные ступеньки марша сделать одинаковой высоты.
Например, пол нижнего этажа облицован керамической плиткой, а пол верхнего этажа выложен паркетом по лагам и фанерному «черному полу». В расчет высоты этажа должны быть включены все слои данных половых конструкций: внизу — толщины выравнивающей стяжки, плиточного клея и плитки; вверху — толщина лаг, фанеры и паркета. В России еще со времен существования СССР высота этажа — величина регламентированная. Обычно стандартная высота этажа равна 2,8 или 3 м, реже — 2,7 или 3,3 м, что позволяет проектировать высоту помещения (расстояние от пола до потолка) не менее 2,4 м. Такая высота этажа позволяют без особого труда вписать лестницу с размерами ступеней, отвечающим требованиям расчетной формулы безопасности (рис. 4, таблица 2). Если ваша высота этажа отличается от нормативной и не кратна 3, то высоту ступеней нужно рассчитывать (округлять) с точностью до одного миллиметра, но так, чтобы высоты всех подступёнков были одинаковыми. Погрешность вычисления, набегающую от округления высот, лучше распределить на нижнюю фризовую ступень, а остальные ступеньки марша сделать одинаковой высоты.
Разные по высоте ступени приводят к постройке травмоопасной лестницы. Особенно опасной эта лестница становится во время спуска в ночное время суток. Спускаясь по лестнице, мышечная память нам подсказывает, что должна быть ступенька. Вес тела переносится на ногу, а ступеньки под ней нет… Она — ниже! И всего-то два-три десятка миллиметров, а ногу подвернули… и еще хорошо, если не покатились кубарем вниз.
В домах с нестандартной высотой этажа для выравнивания высоты ступеней допускается опустить уровень чистого пола верхней этажной площадки чуть ниже относительно уровня чистого пола остального этажа. Порожек лучше не делать, а сделать пол этажной площадки в виде пандуса, то есть наклонным. Для подравнивания высоты ступенек потребуется всего несколько миллиметров так, что уклон будет вряд ли сильно заметным. Как вариант, если лестничная площадка огорожена стенами с дверями, полы между этими помещениями можно сделать с небольшим порогом. Такое решение всем хорошо знакомо: уровень этажных площадок в многоквартирных домах, как правило, ниже уровня чистых полов в квартирах. Ноги мы здесь не ломаем — привыкли.
Ноги мы здесь не ломаем — привыкли.
В таблице 1 рисунка 3 приведены размеры ступеней для «уплотненных» лестниц, пригодных для загородных домов. Нередко в планировках этих домов под лестницы оставляется так мало места, что для того, чтобы сделать лестницу короче, приходится жертвовать шириной проступи. Так, например, в лестнице с высотой подступёнка 200 мм ширина проступи равняется 250 мм. Взрослый человек не может опереться на такую проступь полной ступней и ему приходится спускаться с лестницы боком или спиной вперед. В таблице 2 рисунка 4 приведены размеры высот подступёнков для стандартных высот этажа. Рассчитать ширину проступи по формулам безопасности не составит особого труда. Но есть и еще один способ определить размеры ступеней — графический.
Этот эргономический способ основан на том, что человек, свободно делая по горизонтальной плоскости шаг в 620 мм, может с той же легкостью поднимать ногу на высоту, равную лишь половине этой величины, то есть на 310 мм. Поэтому, если на горизонтальной оси графика (рис. 5) отложить известное число частей, равных каждая одному шагу (620 мм), а на вертикальной оси — равных высоте подъема ноги 310 мм, то такое построение дает возможность получить размеры подъема и ширины ступеней для лестницы с любым наклоном. Для этого нужно нанести на график линию наклона своей лестницы (ее высота и длина известны) и в точках пересечения с сеткой графика провести перпендикуляры. Это и есть оптимальная высота и ширина ступени для данного уклона лестничного марша. Более того, вы можете воспользоваться этим методом и построить лестницу конкретно «по себя». Например, задав шаг равным 600, а подъем соответственно 300 мм либо задав длину шага такой, какой вы считаете нужным.
5) отложить известное число частей, равных каждая одному шагу (620 мм), а на вертикальной оси — равных высоте подъема ноги 310 мм, то такое построение дает возможность получить размеры подъема и ширины ступеней для лестницы с любым наклоном. Для этого нужно нанести на график линию наклона своей лестницы (ее высота и длина известны) и в точках пересечения с сеткой графика провести перпендикуляры. Это и есть оптимальная высота и ширина ступени для данного уклона лестничного марша. Более того, вы можете воспользоваться этим методом и построить лестницу конкретно «по себя». Например, задав шаг равным 600, а подъем соответственно 300 мм либо задав длину шага такой, какой вы считаете нужным.
| Видео (кликните для воспроизведения). |
рис. 5. Графический способ подбора оптимальных размеров ступеней (размеры в мм)
Источники:
- Павлов А. С. Экономика строительства. В 2 частях. Часть 1. Учебник; Юрайт — М., 2016.
 — 316 c.
— 316 c. - Ильин, В. П. Численные методы решения задач строительной механики / В.П. Ильин, В.В. Карпов, А.М. Масленников. — М.: Вышэйшая школа, 2013. — 350 c.
- Чмырь, В.Д. Материаловедение для отделочников-строителей. Материалы для малярных и штукатурных работ / В.Д. Чмырь. — М.: Высшая школа, 1990. — 208 c.
- Белов В. В., Петропавловская В. Б., Шлапаков Ю. А. Лабораторные определения свойств строительных материалов; Издательство Ассоциации строительных вузов — М., 2015. — 200 c.
Размер ступенек по госту
Оценка 5 проголосовавших: 1Здравствуйте! Представляюсь на нашем ресурсе. Я Сергей Винокуров. Я уже более 11 лет занимаюсь застройкой и планировкой помещений. Я считаю, что являюсь специалистом в этом направлении, хочу подсказать всем посетителям сайта как решать сложные и не очень задачи.
Все материалы для сайта собраны и тщательно переработаны для того чтобы донести как можно доступнее всю нужную информацию. Перед применением описанного на сайте всегда необходима обязательная консультация с профессионалами.
гост и способы вычисления. Что такое подступенки
Каждый из нас регулярно имеет дело с лестницей – подниматься или спускаться по ним приходится даже тем, кто живет в высотном доме и предпочитает пользоваться лифтом. Мы чисто автоматически переставляем ноги, поднимая их на требующуюся высоту. И если какая-то ступень выпадает из общего ряда, человек как минимум спотыкается. А то и легкую травму может получить. Но это случается редко: размер ступеней лестницы регламентирован требованием ГОСТа, который при проектировании соблюдается строго. Впрочем, это в интересах как проектировщика (претензий от заказчика не будет), так и пользователя, которому предстоит эксплуатировать лестницу.
Все размеры лестниц четко определены нормами ГОСТа и СНиП. Они дают возможность выбора, поскольку сооружать конструкции приходится в разных исходных условиях. Однако выходить за рамки минимальных и максимальных значений при проектировании разработчики не будут. Так, уклон лестницы не должен превышать 45 градусов, поскольку более крутая конструкция не безопасна для подъема и спуска. Да и пользоваться ею человеку будет тяжело. Идеальным наклоном считается 30 градусов, который и проектируется для общественных зданий. Проблема в том, что лестница, сооруженная под таким углом, занимает слишком много места. Поэтому в частных домах обычно отдается предпочтение более крутым уклонам.
Да и пользоваться ею человеку будет тяжело. Идеальным наклоном считается 30 градусов, который и проектируется для общественных зданий. Проблема в том, что лестница, сооруженная под таким углом, занимает слишком много места. Поэтому в частных домах обычно отдается предпочтение более крутым уклонам.
Особое внимание уделяется ступеням. Стандартный их вариант состоит из двух фрагментов.
- Проступь . Так называется горизонтальная поверхность ступени, предназначенная для установки ноги.
- Подступенок . Вертикальная часть ступени, предназначенная для поддержания проступи. Высота подступенка, собственно, и является высотой ступени.
При проектировании лестницы нормами ГОСТ рекомендуется закладывать высоту подступенка в пределах 12-20 см. Конкретное значение выбирается в зависимости от типа конструкций и их предназначения.
Тонкости маршевых конструкций
Для лестниц в один или несколько маршей идеальной считается ширина проступи (ее еще называют глубиной) в 30 см и высотой ступени в 15 см.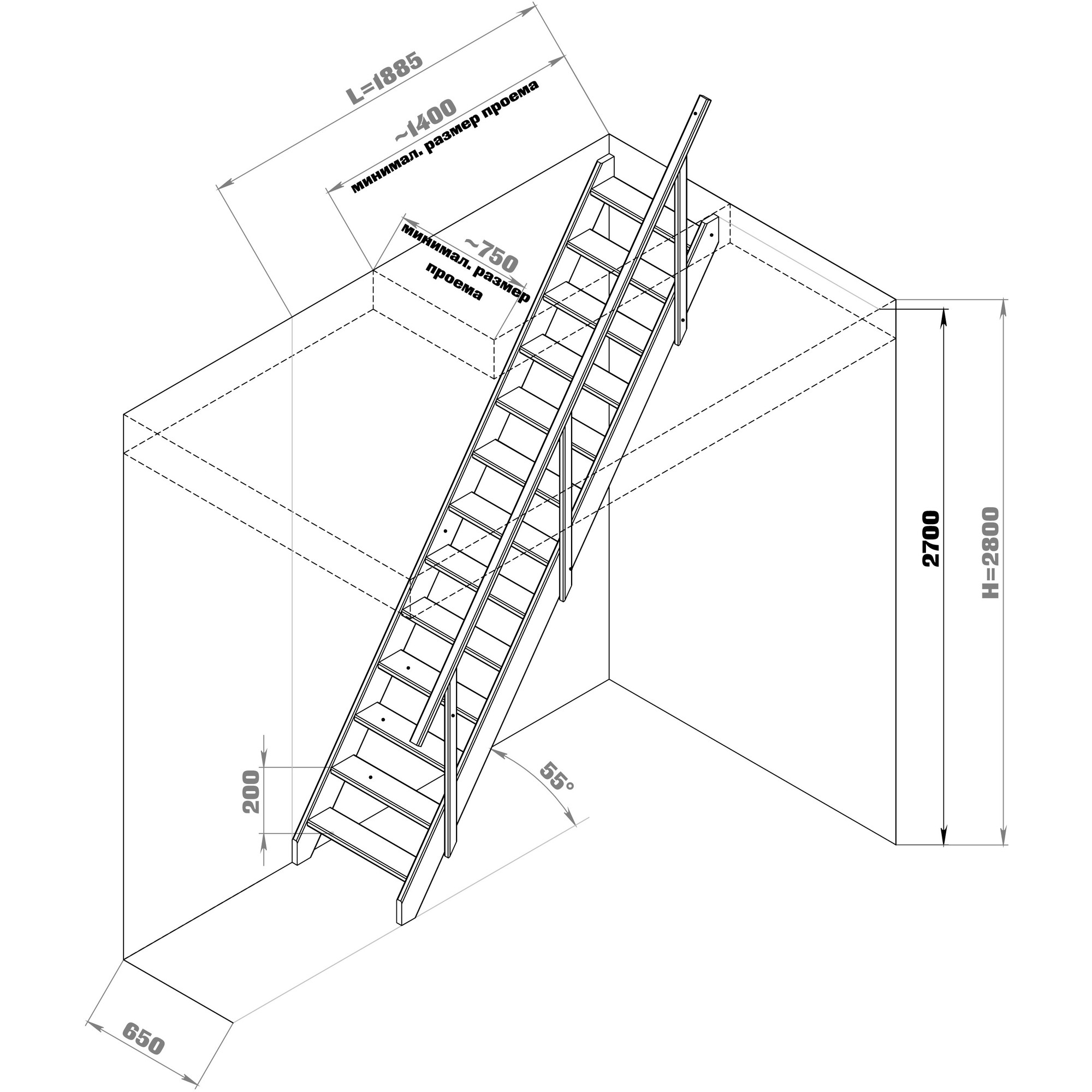 Параметры для маршей выведены, исходя из длины шага среднестатистического человека.
Параметры для маршей выведены, исходя из длины шага среднестатистического человека.
В частном доме, ради экономии пространства, нередко ширину проступи уменьшают до 25, а то и до 20 см. Однако в этом случае рекомендуется проектировать лестницу со сквозными ступенями, то есть не закрывать подступенки материалами. Иначе лестничной конструкцией пользоваться станет крайне неудобно: ширины ступенек на марше для уверенной опоры на проступь будет хватать разве что детям.
Отметим, что правильно сооруженная лестница без подступенков не теряет ни в безопасности, ни в удобстве эксплуатации.
Винтовые конструкции
Когда в доме монтируется винтовая лестница, к ее ступенькам предъявляются несколько другие требования, хотя основные стандарты по-прежнему остаются в силе. Такая лестница значительно экономит пространство, однако ступени на ней по форме и расположению сильно отличаются от тех, что ставятся на маршах конструкций маршевого типа. Обычно при проектировании винтовой конструкции соблюдается два правила.
- Ширина ступени выбирается в пределах 20-22 см. В противном случае придется делать слишком широкий изгиб, что в условиях ограниченности пространства чаще всего неприемлемо.
- Из-за недостаточной глубины ступеней подступенок по правилам не оборудуется.
Исключением в плане указанных параметров могут быть лестницы, выполненные в винтовом варианте исключительно из дизайнерских соображений. Тогда и ширина самой конструкции, и глубина ступеней выбираются в более комфортных для эксплуатации параметрах.
Расчет размеров ступенек лестницы
Высота подступенка, глубина самой ступени – все эти параметры напрямую влияют на удобство пользования конструкцией. Наиболее удобной высотой ступени считается диапазон между 14 и 17 см, максимальной допустимой – показатель в 20 см. Оптимум высчитывается в зависимости от высоты помещения, где монтируется лестница, но всегда зависит от размера шага человека.
Если речь идет о лестничной конструкции, ведущей к входной двери, разработчик может отклониться от рекомендуемых размеров: очень часто такие лестницы оборудуются с повышенной глубиной ступеней и малой их высотой. Такой ход повышает безопасность пользования лестницей при плохих погодных условиях.
Такой ход повышает безопасность пользования лестницей при плохих погодных условиях.
Для расчета ширины шага лестничной конструкции, расположенной внутри дома, имеется простая формула: 2а + в = 60. В ней а – ширина ступени, в – ее высота. При проведении расчетов иногда приходится перебирать несколько вариантов параметров, чтобы определиться с идеальным размером ступеней лестницы.
Что касается количества ступеней, то его рассчитать, пожалуй, проще всех остальных параметров.
- Замеряется высота помещения. За нее принимается дистанция от чистового покрытия нижнего этажа до такого же уровня верхнего.
- Выбирается оптимальная высота ступени.
- Первый параметр делится на второй – получаем количество ступеней.
По поводу числа этих элементов ГОСТ ничего не говорит. Однако чисто практически и психологически более комфортным считается нечетное их количество – начинать и заканчивать подъем удобнее с одной и той же ноги. Поэтому если в результате расчетов вы получили четную цифру, следует подумать об ее изменении. Можно нижнюю или верхнюю ступеньку сделать не стандартной высоты (чуть более низкой или высокой), чтобы увеличить или уменьшить количество ступеней на единицу.
Можно нижнюю или верхнюю ступеньку сделать не стандартной высоты (чуть более низкой или высокой), чтобы увеличить или уменьшить количество ступеней на единицу.
Безопасность и комфорт эксплуатации лестничной конструкции зависит также от соотношения глубины проступи и высоты проступенка. При сложении этих параметров проектировщик должен получить 46 см (плюс-минус сантиметр).
А чтобы проверить, насколько удобно будет безопасно подниматься и спускаться по лестнице, можно из ширины лестницы отнять ее высоту. Если на выходе получается 12 см, значит, вы разработали идеальную конструкцию.
Особенно важно скрупулезно просчитать шаг ступенек конструкции. С него, собственно, и стартуют прочие расчеты. Неверно рассчитанный шаг при эксплуатации лестницы может даже повлечь за собой плохое самочувствие пользователей, особенно находящихся в пожилом возрасте: избыточное перенапряжение, необходимое для сбережения равновесия, ведет к болезненным ощущениям в ногах.
Чтобы не затруднять себя возней с калькулятором, можете воспользоваться бесплатным онлайн сервисом, который рассчитает вам все необходимые параметры лестницы, в том числе и размеры ступеней:
Споры между сторонниками и противников подступенков в лестничном деле не утихают ни на минуту. Вопрос вкуса – делать лестницу открытой или закрытой, и у каждого на этот счет свое мнение. Мы все же постараемся разобраться, в каких случаях подступенки действительно нужны и зачем, а в каких без них лучше обойтись.
Вопрос вкуса – делать лестницу открытой или закрытой, и у каждого на этот счет свое мнение. Мы все же постараемся разобраться, в каких случаях подступенки действительно нужны и зачем, а в каких без них лучше обойтись.
Что такое подступенки и зачем они нужны?
В первую очередь, стоит сказать о том, что же такое подступенки. Это небольшие деревянные дощечки, которые устанавливаются под ступень, отсюда и проистекает их название. Подступенки являются классическим элементом лестницы. Их использовали, начиная с древнейших времен в качестве возможного способа скрыть пространство под лестницей. Чаще всего там располагалась еще одна комната или кладовая.
Если ваша цель – создать кладовку, личный кабинет, библиотеку или любое другое подобное пространство, то вариант с подступенками подойдет вам лучше всего. Лестница получится монолитной, цельной, изолированной от любопытных взглядов. Изнутри можно провести освещение и наслаждаться книгами в тишине. Главное, чтобы ступени при этом не скрипели под шагами, иначе спать в этой комнате будет невозможно.
Когда еще применяются подступенки?
Когда в дело вступают художники и просто творческие люди. Подступенки превращают в настоящее произведение искусства, ведь никакой нагрузки на них не идет, они практически не изнашиваются, а краска на них не стирается. При взгляде на лестницу снизу вверх создается впечатление, что читаешь книгу или просматриваешь иллюстрированный журнал.
Подступенки могут служить дополнительным декоративным элементом при формировании необычного помещения. Например, стеклянные лестницы часто делают с подступенками, чтобы дополнительно их обезопасить, не потеряв, при этом, в эстетичности.
Когда подступенки будут лишними?
Совершенно точно, если вы хотите сделать винтовую лестницу из кованого металла, подступенки будут лишь отвлекать от основной идеи проекта. Они не применяются в больцевых системах или в лестницах на одном центральном косоуре. В этом случае подступенки ограничивают легкость конструкции, которая должна просматриваться в каждом ее элементе.
Не нашли применения подступенки и во многих авангардных проектах лестниц, в лестницах на тетивах, выполненных с забежными ступенями и в нескольких других видах необычных лестниц.
Выводы и итоги
Если вы придерживаетесь идеи лестничной классики и хотите видеть в своем доме красивую маршевую лестницу, то подступенки хорошо вам подойдут.
Если вы ищите новых, авангардных и нестандартных решений, подступенки будут только мешать вам.
В результате, выбор того или иного варианта зависит от того, что вы хотите увидеть в своей домашней лестнице.
Какого бы типа не была лестница и из какие бы материалы не применялись для ее изготовления, одно остается неизменным – конструкция должна быть удобной и безопасной в эксплуатации. В том случае, когда вы приобретаете уже готовое изделие в строительном маркете, все необходимые требования и ГОСТы, предъявляемые к системе, уже соблюдены инженерами-проектировщиками и изготовителями. Но как быть, есть вы сооружаете лестницу собственными силами? Все очень просто – внимательно изучите инструкцию по расчету оптимальных комфортных размеров конструкции и без ошибок рассчитайте такие нужные параметры системы, как высота ступени и подступенка. А поможет вам в проведении расчетно-проектировочных работ подробная инструкция, приведенная в этой статье, проиллюстрированная качественными фото и полезным видео.
А поможет вам в проведении расчетно-проектировочных работ подробная инструкция, приведенная в этой статье, проиллюстрированная качественными фото и полезным видео.
Комфорт и безопасность вашей лестницы напрямую зависят от того, на сколько оптимально правильно произведен расчет таких параметров, как высота и ширина ступеней и подступеньков
Основные конструкторские требования к лестнице
Лестничная конструкция, которую вы планируете соорудить в своем доме, должна отвечать существующим ГОСТам по таким параметрам:
- высоте;
- ширине;
- углу наклона;
- размерам ступенек и подступеньков.
Оптимальная высота проступи, согласно ГОСТу, должна быть в пределах от 16 до 19 сантиметров
Ранее в предыдущих публикациях мы уже рассматривали, как правильно рассчитать основные параметры лестничных маршей. Сегодня же поговорим о том, как без ошибок вычислить размеры ступеней и подступенек для сооружаемой лестницы в доме.
На рисунке представлены оптимальные размеры конструкции для удобного перемещения по ней человека
Но для начала ознакомимся с наиболее популярными ошибками, которые допускают начинающие строители при монтаже лестничной системы своими руками.
Все ступени изделия должны быть строго одинакового размера, что обеспечит безопасность и удобство передвижения по лестнице
Ошибки при расчете высоты ступеней
В соответствии с общепринятыми нормами, высота ступи не должна быть более 19 см. В противном случае передвижение по лестнице с высоким подъемом будет достаточно некомфортным, в особенности для детей и людей пожилого возраста.
При проведении необходимых расчетов для определения размеров ступеней, для наглядности воспользуйтесь приведенной на фото схемой
Высота ступени согласно ГОСТ
Согласно с требованиями ГОСТ, допустимый показатель высоты ступеней должен быть:
- для лестниц, расположенных в частных домах, на дачах, в многоуровневых квартирах – 19 см;
- для нежилых помещений – 17 см.
Однако, если ваша планировка не позволяет выполнить установленный норматив, тогда в редких случаях допускается коррекция высоты до 20 см, но не более.
На фото продемонстрирован принцип проведения расчетных действий при проектировании лестницыСтупени разного размера
Неодинаковая вышина ступеней лестницы может стать причиной даже несчастного случая. Поэтому при строительстве очень важно не экспериментировать в этом направлении, а делать ступени в соответствии с требованиями комфортными и одинаковыми по размеру.
Поэтому при строительстве очень важно не экспериментировать в этом направлении, а делать ступени в соответствии с требованиями комфортными и одинаковыми по размеру.
При возведении конструкции старайтесь придерживаться установленных стандартных величин
Стандарты
Строительство, независимо от предназначения возводимого объекта, должно осуществляться при строгом соблюдении установленных норм и ГОСТов. Это правило в первую очередь касается и начинающих застройщиков, которые любят поэкспериментировать. Поэтому каждый строитель, принимаясь за работу, должен четко усвоить – при сооружении любого объекта необходимо строго придерживаться уже существующих норм и стандартов.
Стандартный шаг взрослого человека составляет около 55 — 60 сантиметров при передвижении по ровной поверхности, при подъеме по лестнице этот показатель практически вдвое меньше
При расчете высоты проступи не забывайте учитывать толщину материала изготовления
Определяем высоту ступени и подступенка – инструкция по расчету
Профессиональные строители советуют новичкам не экспериментировать при проведении расчетных работ, а лучше воспользоваться уже проверенными готовыми формулами для вычисления оптимальных и комфортных размеров конструкции. Одной из таких формул является математическое выражение для определения оптимальных комфортных значений высоты и ширины ступеней. Данная формула имеет вид:
Одной из таких формул является математическое выражение для определения оптимальных комфортных значений высоты и ширины ступеней. Данная формула имеет вид:
А+Б = 450 ± 20 мм, где:
Б — ширина проступи,
Лестница является важным элементом любого дома. Она бывает различных типов, может быть расположена внутри либо снаружи здания. Главными требованиями к подобной конструкции предстают надежность и комфортное использование. Чтобы человек, перемещающийся по данной лестнице, не чувствовал дискомфорта, необходимо уделить особое внимание размерам проступи и подступенка.
Что такое проступь и подступенок?
Под данными терминами понимаются вертикальные и горизонтальные элементы ступени. Подступенком называется её высота. Чтобы лестница была максимально комфортной и безопасной, высота подступенка должна находиться в интервале 15-18 сантиметров, при этом двойная высота данного параметра, которая сложена с размером проступи (горизонтальной частью ступени), должна быть равна среднему шагу человека. По статистике данный параметр должен находиться в пределах 60-64 сантиметров.
По статистике данный параметр должен находиться в пределах 60-64 сантиметров.
СНиП предусматривает следующие оптимальные размеры:
- когда речь касается жилых и общественных помещений, подступенок должен быть равен 14,8 сантиметра, а для подвалов и чердаков – 17,1 см;
- проступь должна иметь ширину 30 и 26 сантиметров соответственно.
Основные требования
Изготавливаемая лестница должна отвечать установленным параметрам ГОСТа касательно:
- высоты;
- ширины;
- угла наклона;
- размера ступеней и подступенков конструкции.
Рассмотрим оптимальные размеры элементов лестницы.
- Маршевая площадка должна иметь минимальную ширину 80 сантиметров. Измеряется она от поверхности стены, учитывая толщину отделки, до внутренней стороны поручней.
- Ширина марша, который будет удобен для человека, находится в пределах от 90 до 100 сантиметров. Необходимо учесть то, что один марш не должен включать в себя более 17-ти и не менее 3-х ступеней.

- В качестве оптимальной высоты ступеней приняты параметры в 17 см, но не менее 12 см.
- Оптимальная ширина ступеней находится в интервале 25-32 см.
Подступенок может быть готовым или сделанным самостоятельно. Сегодня часто применяются керамические изделия или варианты из МДФ, светлые с темными или белыми полосами.
Часто встречаемые ошибки
Прежде чем начать непосредственное выполнение строительства лестницы, вы обязательно должны ознакомиться с наиболее встречаемыми ошибками, которые часто возникают при установке лестниц самостоятельно. В данном случае стоит выделить некоторые.
- Неправильная высота ступеней. Существующие на сегодня стандарты предусматривают, что она не должна превышать 19 сантиметров, иначе конструкция будет неудобной для использования. Такие ступени доставят дискомфорт маленьким детям и пожилым людям. Когда речь касается жилых помещений, максимальная высота ступени равна 19 см, а для нежилых зданий 17 см.
 Необходимо обратить внимание на то, что если особенность планировки не допускает соблюдение данных параметров, допускается скорректировать высоту ступени до 20 см.
Необходимо обратить внимание на то, что если особенность планировки не допускает соблюдение данных параметров, допускается скорректировать высоту ступени до 20 см. - Неодинаковый размер ступеней. Разница в высоте и ширине может привести к несчастным случаям.
Если они будут разными, то будет нарушен оптимальный ритм ходьбы человека.
Инструкция
Специалисты в области строительства лестничных конструкций не советуют новичкам экспериментировать при расчетных работах. Рекомендуется использовать проверенные формулы, благодаря которым вы сможете определить оптимальные и комфортные размеры конструкции. Считается, что высота и ширина ступеней в сумме должны составлять 43-47 см.
Определяем ширину ступеней и их количество. Этот параметр лучше всего рассматривать на конкретном примере.
Этапы выполнения расчёта следующие. В первую очередь необходимо измерить расстояние от пола до потолка. В нашем примере мы возьмём за основу 2,5 метра. Межэтажное перекрытие составляет в нашем случае 35 см.
Межэтажное перекрытие составляет в нашем случае 35 см.
В результате высота нашей конструкции будет составлять сумму двух предыдущих параметров, а именно 2,85 метра. Высота подступенков, предусмотренная стандартом, равна 17 сантиметрам. Мы будем придерживаться данного параметра. Необходимо определить количество требуемых ступеней посредством деления высоты лестницы на 17 см. В нашем случае число ступеней будет при округлении равно 17 штукам.
Определять высоту проступи необходимо, базируясь на том, в какой сфере будет использоваться наша конструкция. Существует несколько вариантов.
- Лестничная конструкция для частных домов, дач и квартир. В данном случае высота подступенка должна равняться 15,5-22 см, а проступь находиться в интервале 24,5-26 см.
- Для общественных зданий лестничные подступенки должны быть немного ниже. Они должны равняться 13,5-18 см. При этом проступь шире, чем в жилых зданиях, то есть 28-34 см.
- В иных помещениях стандартной высотой подступенка является 15-19 сантиметров, а ширина проступи должна находиться в интервале от 25 до 32 см.

Особое внимание также требуется уделить оптимальному наклону лестницы. К сожалению, строительных стандартов в данном вопросе нет. Уклон лестницы базируется на том, какое соотношение будет у подступенка и проступи. Делается упор на максимальную и минимальную высоту и глубину ступени. Исходя из данных параметров, базируясь на размерах проступи и подступенка, можно отметить, что угол наклона колеблется в интервале от 33 до 45 градусов. Когда дело касается внутренних лестниц, то данное значение должно быть до 38 градусов. Когда речь идет о подсобных либо чердачных лестницах, которые характеризуются более крутым спуском, оптимальный угол наклона равен до 45 градусов.
Вы должны учитывать, что, чем шире угол наклона, тем больше пространства будет занимать лестничная конструкция.
Для чего нужны точные расчеты?
Важно, чтобы параметры каждой ступени в лестничной конструкции были максимально точными и одинаковыми. Это позволит человеку подниматься и спускаться по лестнице без особой осторожности, базируясь на мышечной памяти ног. Если установленные правила не будут соблюдены, человек будет испытывать дискомфорт при пользовании лестницей. Особо остро это ощущается, когда ступени имеют разную высоту.
Это позволит человеку подниматься и спускаться по лестнице без особой осторожности, базируясь на мышечной памяти ног. Если установленные правила не будут соблюдены, человек будет испытывать дискомфорт при пользовании лестницей. Особо остро это ощущается, когда ступени имеют разную высоту.
В подобной ситуации часто встречаются травмы. Если вы будете осуществлять правильный расчёт подступенков, то сможете избежать различных повреждений.
Соблюдение существующих норм и правил касательно строительства лестничных конструкции позволят сделать ее максимально безопасной и удобной.
Крепление подступенков
Данный процесс может быть осуществлён различными способами. Это зависит от того, из какого материала изготавливается ваша лестница, при этом учитывается, будет ли он снизу подшиваться. На параметр крепления оказывает влияние и устройство косоуров.
Существует три основных способа выполнения крепления. Рассмотрим каждый из них.
- Классическая установка, где крепление осуществляется в паз.
- Крепление, выполняемое к торцу, с помощью использования саморезов. Этот же способ предусматривает установку фурнитуры с применением клея.
- Монтаж подступенков с задействованием уголка.
Останавливать свой выбор на том или ином способе вы должны, базируясь на собственных предпочтениях и сфере использования лестничной конструкции.
При строительстве лестницы обязательно учитывайте наиболее действенные советы специалистов.
- Для того чтобы осуществить замену проступи , рекомендуется снять старые плоские элементы ступеней, расположенные сверху. Следите, чтобы клин не сместился при использовании.
- Если клин был потерян, элемент можно будет опереть на брусок. Плоские элементы лестницы нужно располагать внахлёст. Таким образом, они частично будут друг друга перекрывать, если посмотреть на них сверху. Их ширина может быть неодинаковой в местах, которые служат для опоры правой и левой ноги.
 Для того чтобы установить ограждение, требуется высверлить отверстия по краям ступеней.
Для того чтобы установить ограждение, требуется высверлить отверстия по краям ступеней.
Лестница, отделанная ламинатом, хорошо смотрится в любом интерьере вне зависимости от его стиля Далеко не каждый лестничный стройматериал подойдет для создания ступенек. Обшивка лестничной конструкции ламинатной доской сегодня достаточно актуальна, так как этот отделочный материал имеет все качества, которые нужны для создания высококачественного покрытия поверхностей. В материале представлен разбор того, как обшить лестничную конструкцию своими руками, а также рассмотрены достоинства материала и нюансы работы.
Практичная отделка ламинатом бетонной лестницы
Ламинатная доска – это напольное покрытие на основе ДВП (из фанеры). Жёсткие ламинатные плиты достаточно надежны, способны выдержать сильные нагрузки, что возможно из-за слоистой структуры. Ламинат состоит из 4 слоев.
Главная задача самого нижнего слоя – обеспечение защиты материала от разного рода деформаций. Это слой-стабилизатор, который повышает жёсткость. В некоторых разновидностях стройматериала к нижнему слою приклеивается звукоизолирующий слой, это дает возможность напольному покрытию отлично устранять лишний звук. Несущий слой – это основа доски. Его создают из древесноволокнистой плиты, которая имеет очень высокую плотность. Именно этот слой наиболее значимый в конструкции, так как выполняет важнейшие функции.
Это слой-стабилизатор, который повышает жёсткость. В некоторых разновидностях стройматериала к нижнему слою приклеивается звукоизолирующий слой, это дает возможность напольному покрытию отлично устранять лишний звук. Несущий слой – это основа доски. Его создают из древесноволокнистой плиты, которая имеет очень высокую плотность. Именно этот слой наиболее значимый в конструкции, так как выполняет важнейшие функции.
Если помещение небольшое, то лестницу лучше обивать ламинатом светлого цвета
Именно в этом слое присутствует замок, который и дает возможность ламинату скрепляться между собой.
Также несущий слой является основным шумоизолятором. И наконец, влагоустойчивость ламината в прямой зависимости от этого слоя. Он пропитан специальными веществами, которые обеспечивают защиту от влаги. Декоративный слой обеспечивает внешнюю привлекательность материала, которым выполняется облицовка.
Слой представлен бумажным листом, на который нанесен рисунок, имитирующий поверхность:
- Паркетной доски;
- Дерева;
- Кафеля;
- Натурального камня.

На самом верху доски расположен слой-защита. Это спецпокрытие акрилом или меламиновой смолой, которая дает защиту от механических воздействий. Класс износоустойчивости зависит от этого слоя, но в наше время у него появилась и функция декора. На его поверхность накладывается фактура, и это лучше имитирует дерево, линолеум, структуру паркета.
Специалисты дают несколько рекомендаций по монтажу ламината своими руками. Первая ступенька обычно отличается от других ступеней, так как значительно выступает за тетиву лестницы сбоку, поэтому правильно будет сделать шаблон из картона, по которому будут вырезаться пластинки. Так получится сэкономить стройматериал.
Если, выкраивая ступени маршевой лестничной конструкции, сложностей не будет, то можно резать элементы для винтовой лестницы.
Среди достоинств лестниц из ламината стоит отметить отличный внешний вид и хорошие эксплуатационные качества
В обязательном порядке надо сделать шаблоны. При этом, замерять надо отдельно каждую ступеньку, и переносить форму на картон. Если этого не сделать, то будет много брака. Прочное покрытие возможно получить, только если отделать конструкцию полностью, так как укладка делается не только для декора, но и носит декоративную функцию. Обшитая по правилам конструкция прослужит долго. Такой лесенкой можно будет наслаждаться многие годы.
При этом, замерять надо отдельно каждую ступеньку, и переносить форму на картон. Если этого не сделать, то будет много брака. Прочное покрытие возможно получить, только если отделать конструкцию полностью, так как укладка делается не только для декора, но и носит декоративную функцию. Обшитая по правилам конструкция прослужит долго. Такой лесенкой можно будет наслаждаться многие годы.
Ламинат имеет неоспоримые достоинства:
- Большой выбор цветов и фактур, поэтому обшитая ламинатом лестница, способна украсить интерьер любого стиля.
- Легкий монтаж и ремонт.
- Приемлемые расценки.
Ламинатная доска для лестничной конструкции на второй этаж должна соответствовать требованиям – износостойкость для поддержания эстетичности лестницы на протяжении многих лет, надежность, так как с годами при эксплуатировании лестница будет подвергаться ежедневным нагрузкам и антискользящая поверхность, которая гарантирует безопасность при спуске и подъеме. Ламинат для лестницы – идеальный и долговечный вариант. Дольше прослужит, если устроить уголок и плинтус.
Дольше прослужит, если устроить уголок и плинтус.
Подготовительный этап сборки ступеней из ламината
Если есть желание покрыть лестницу ламинатом, то важно понимать, плиты не способны укрепить расшатанные ступени. Им самим нужна надежная основа. Лестница может быть металлической, бетонной или деревянной.
И даже, если ступени крепкие и надежные, но имеется люфт, ламинатные доски будут:
- Расползаться;
- Деформироваться;
- Разъезжаться.
При этом, на клей плиты «садить» запрещено, так как они могут растрескаться. Толщина плит должна быть 6-12 мм, поэтому такой стройматериал может стать надежным покрытием, но не основанием. Предусматривая ступеньки, обшитые ламинатом, мастер обязательно должен хорошо укрепить подступенки и проступи на крепежи, исключая любой люфт.
До того как обшивать ламинатом, все сомнительные элементы конструкции надо укрепить.
Если перед облицовкой были сделаны какие-то лакокрасочные работы, то основа должна высохнуть и только потом можно делать монтаж.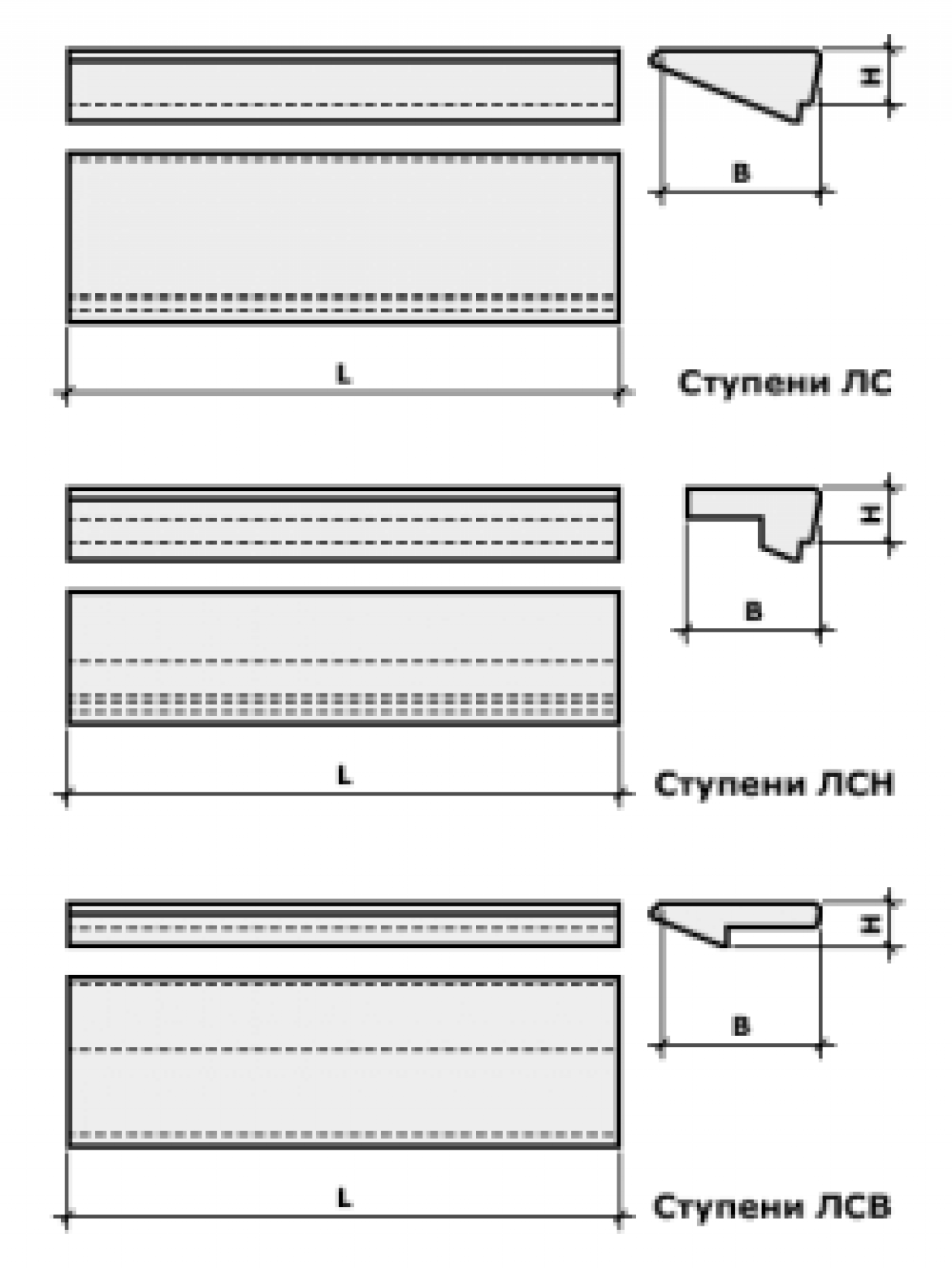 Как только крепежи вкручивается в древесную поверхность, над шляпкой самореза остается небольшое углубление. Для того чтобы крепеж не покрылся ржавчиной, её надо укрыть чопиками (деревянный элемент) или же зашпаклевать.
Как только крепежи вкручивается в древесную поверхность, над шляпкой самореза остается небольшое углубление. Для того чтобы крепеж не покрылся ржавчиной, её надо укрыть чопиками (деревянный элемент) или же зашпаклевать.
Проведение монтажа плинтуса для лестницы
Теперь необходимо подробно рассмотреть, как обшить лестничную конструкцию ламинатом квик степ (quick step). Прежде чем обшивать, нужно понять, что лучшее качество возможно получить только тогда, когда каждая ступень будет обшита одной плитой, не имеющей стыков. То есть, одна доска идет на проступь и одна на подступенок. Сегодня возможно запросто купить ламинат по ширине проступи.
Если лестница имеет много маршей, то на площадках нужно устраивать плиты замок в замок.
Любая упаковка ламинатной доски содержит инструкцию, где подробно описано, что перед монтажом, под плиты следует уложить подложку. Такая мера даст возможность не только утеплить пол, но и устранить лишний звук. В качестве шумоизолятора возможно применять 2-х миллиметровую подложку из ПЭ. У данного изолятора есть неоспоримые достоинства, стоимость и хорошее устранение шумов.
В качестве шумоизолятора возможно применять 2-х миллиметровую подложку из ПЭ. У данного изолятора есть неоспоримые достоинства, стоимость и хорошее устранение шумов.
Чтобы подогнать панели под ступеньки, хорошо работать электрическим лобзиком, который имеет пилку по древесине. Но, если элементы полукруглые, фигурные, например, под балясину, то нужно использовать узкую и надежную пилку по металлу.
Также панели можно порезать, используя:
- Ножовку;
- Ручную циркулярную пилу;
- Или болгарку.
Благодаря плинтусу можно существенно улучшить эстетические качества лестницы из ламината
После того как шумоизолятор уложен, можно монтировать к ступенькам ламинат. Собственно облицовка лестничной конструкции ламинатом представляет собой простую работу. Для этого могут быть применены крепежи, которые должны быть из цветных металлов, чтобы не заржаветь. Вполне достаточным будет закрутить по каждому краю проступи по 1 крепежу, так как доски будут крепиться на уголки из металла.
Подступенки устраиваются также. То есть, с обоих краев ламинат крепится к основе на крепежные элементы. Так как основная нагрузка на покрытие приходится на край ламинатной доски, то для его защиты, применяется лестничный профиль для ламината. Если такой профиль не смонтировать, то в скором времени покрытие придет в негодность. Металлический уголок тоже выступит в качестве защиты от повреждений, сохранит эстетичность.
Возможные проблемы с уголком для ламината
При отделке лестницы плитами, многие встречаются с некоторыми проблемами. Первая ступень обычно отличается от других, так как сбоку, как уже отмечалось, она серьезно выступает за тетиву. В этом случае применяют шаблон, размеры которого позволяют правильно разрезать доски ламината, чтобы не допустить перерасход стройматериала.
При обшивке прямого марша, определение формы ступеней не проблематично. В случае, если есть желание обшить винтовую лестницу, тогда для каждой ступеньки надо сделать отдельный картонный шаблон. Работа кропотливая, но результат будет великолепный. Все ступеньки должны быть полностью укрыты плитами, только так можно сделать надежное покрытие.
Работа кропотливая, но результат будет великолепный. Все ступеньки должны быть полностью укрыты плитами, только так можно сделать надежное покрытие.
Отделка лестницы ламинатом своими руками (видео)
Прислушавшись к советам опытных мастеров, можно самостоятельно выполнить облицовку и ходить по надежной, красивой лестнице.
Примеры отделки лестницы ламинатом (фото идей)
Круглая лестница из бетона
Круглые лестницы на второй этаж часто являются логичным решением для обустройства двухъярусных квартир и частных домов. У них есть несколько серьезных достоинств, и всего один недостаток. Такие лестницы идут вокруг оси, однако при изготовлении из железобетона установка опорного столба не обязательна. Их главное отличие от винтовых аналогов – лестничный марш не заходит на спираль, а заканчивается в пределах одного круга.
Характеристика лестниц
Купить круглую лестницу стоит потому, что она имеет следующие достоинства:
- вся конструкция занимает минимум жилой площади;
- стоит несколько дешевле за счет экономии материалов;
- отлично вписывается в интерьер любого стиля.

Именно круглая лестница за счет своей конфигурации умещается на небольшой площади. Поэтому её устанавливают в зданиях, где каждый квадратный метр имеет значение.
Укладка ламината на пол, от выбора до монтажа.
Решение оптимально и для второстепенных подъемов, редко использующихся (на чердак, спуск в подвальное помещение). Расходы на установку ниже, ведь в большинстве случаев и материалов на изготовление конструкции требуется меньше.
Экономичными и качественными, долговечными считаются круглые лестницы из бетона. Такое изделие можно спроектировать с учетом всех особенностей объекта, идеально встроить в жилое пространство и сделать не только удобным, демократичным по стоимости, но и красивым. Поверх железобетонной конструкции можно пустить любые отделочные материалы, общий вид интерьера будет смотреться стильно и дорого.
Выбирая декор и вид отделки, легко адаптировать решение под любой стиль интерьера. Больше фото круглых бетонных лестниц можно увидеть в каталоге наших работ.
На что следует обратить внимание
Так как вся конструкция состоит из забежных ступеней, усеченных у оси, такую формы не сделать узкой. Длина каждой ступени должна быть не меньше метра, и все же передвигаться по ней быстро не получится, поэтому категорически не рекомендуется оборудовать такой лестницей подъем в детскую комнату. В быту такая лестница подходит только для помещений, куда нужно подниматься не слишком часто.
Техника безопасности в подобных конструкциях приобретает особое значение: перила должны быть удобными, функциональными для людей разного роста. Сами ступени обязаны быть нескользкими, удобными по ширине, к внешнему краю они должны вмещать стопу взрослого человека. Чтобы спуск и подъем были комфортными и безопасными. Поэтому заказывая круглую бетонную лестницу, обсудите с инженером в деталях, как именно и кем она будет использоваться.
Цена круглой лестницы будет зависеть, прежде всего, от выбора материалов. Однако грамотно спланированная конструкция визуально кажется легкой, изящной, она украсит любое жилище.
Изготовленная нашей командой круглая лестница будет удобной и безопасной в эксплуатации для всех членов вашей семьи. Позвоните нам по указанным телефонам или оставьте заявку на обратный звонок, и мы сможем дать подробную консультацию о цене и особенностях установки круглой лестницы на второй этаж.
Как мы работаем
Что такое подступенки и для чего они нужны
Многие владельцы частных домов с лестницами задаются резонным вопросом: «для чего все-таки нужны эти подступенки?». С одной стороны – это эстетичное и практичное решение, нос делать лестницу с ними довольно сложно.
Особенности отделки лестницы ламинатом
В этом плане подступенки вызывают много споров. Постараемся ответить на вопросы о том, что это такое, для чего они нужны и нужны ли вообще.
Что такое подступенки?
Подступенки – это небольшие доски, которые устанавливаются с торца каждой ступени и располагаются как бы под ними. От этого своего местоположения они и получили основное название. В большинстве случаев подступенки выполняются из того же материала, что и основная лестница, но, если декоративное решение требует иного, например, контрастного сочетания, они могут выполняться из другого дерева.
В большинстве случаев подступенки выполняются из того же материала, что и основная лестница, но, если декоративное решение требует иного, например, контрастного сочетания, они могут выполняться из другого дерева.
Подступенки – очень важный элемент лестницы, как таковой. Они не позволяют ноге проваливаться внутрь, застревать. Это очень важно для пожилых людей и маленьких детей, которые постоянно норовят везде засунуть свои ножки, ручки и даже голову, чтобы посмотреть, что же там под лестницей.
То есть подступенки выполняют и декоративную и практическую функцию.
Для чего нужны подступенки
Некоторые владельцы собственного жилья не представляют себе лестницу без подступенков. Это классический элемент любой большой и красивой лестницы на второй этаж. Если вы цените добротность и основательность, то подступенки – это ваш выбор. С другой стороны, особой практической функции они не несут. В некоторых открытых по виду конструкциях, они лишь портят общее впечатление от лестницы.
Нужны ли подступенки?
Если вы придерживаетесь классической, глухой модели лестницы, то, безусловно, нужны. Если же у вас установлена красивая, воздушная и очень современная лестница, то подступенки будут лишним декоративным элементом, который очень сильно испортит впечатления от лестницы. Подступенки обычно устанавливают в классических деревянных решениях из дорогого дерева. В то же время, металлические лестницы в большинстве своем идет без подступенков.
Стоит отметить, что лестницы с забежными ступенями могут быть, как с подступенками, так и без них, а вот винтовые конструкции практически всегда выполняются открытыми.
Делать ли подступенки или нет – личное дело каждого владельца своего жилья. Самое главное – определить для себя, нужны ли вам подступенки или нет, насколько внешний вид вашей лестницы приближен к классике и не будут ли они мешать вам при передвижении.
Размеры лестниц
Размеры лестниц должны выбираться таким образом, чтобы размеры ступеней соответствовали бы движению человека при ходьбе.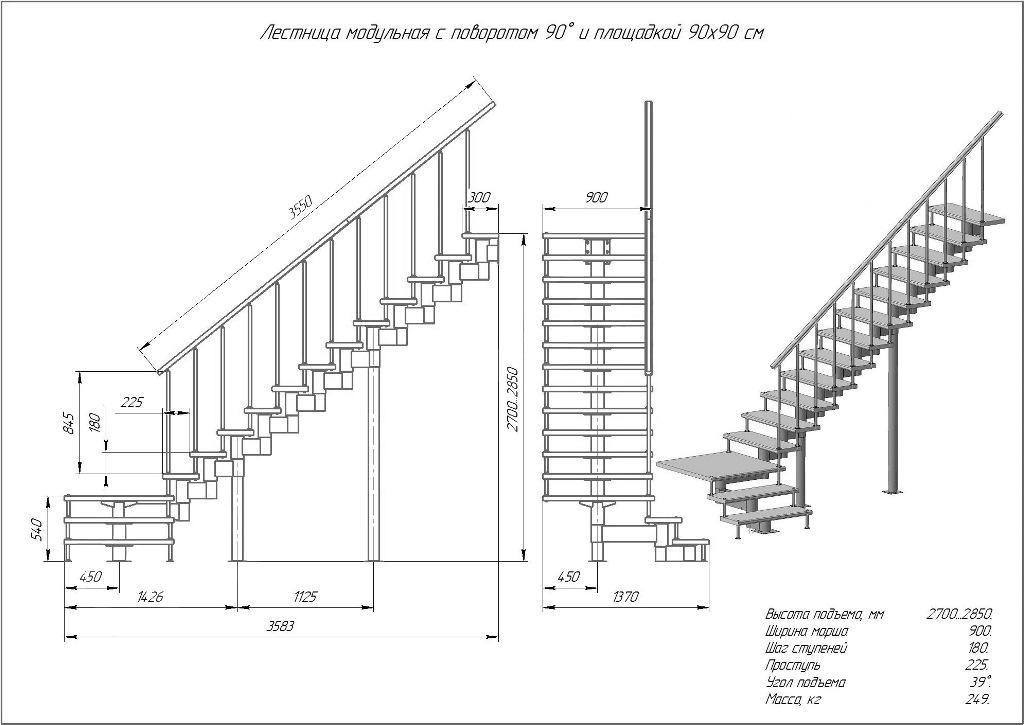
Размеры лестниц складываются из размеров ступеней. В случае спиральных лестниц требуется смещение ступеней.
Размеры ступеней
- Высота подъема ступени — это вертикальный размер s между проступями следующих друг за другом ступеней (рис. 1).
- Ширина проступи — это горизонтальный размер а, измеренный между передними гранями двух, следующих друг за другом ступеней.
- Отношение подъема — называют отношение высоты подъема к ширине проступи s/a. Эта величина определяет уклон лестницы.
- Подрезка — это горизонтальный размер и, на который передняя грань ступени выступает над шириной проступи нижележащей ступени.
Рис. 1. Размеры ступеней
В зависимости от высоты подъема ступени (высоты подступенка ) ходьба по лестнице напрягает человека в большей или меньшей степени. Кроме того, имеет значение, как часто ходят по данной лестнице. Высота подъема ступени — это важный размер для проектирования лестницы. При этом следует придерживаться указаний, приведенных в табл. 1.
При этом следует придерживаться указаний, приведенных в табл. 1.
Ширина проступи должна составлять от 25 до 32 см. При ширине проступей менее 26 см для увеличения площади, куда можно поставить ногу, возможно устройство подрезки до 3 см. В случае массивных каменных ступеней это возможно с помощью устройства выкружек или скосов плит ступеней, которые соответствующим образом увеличиваются по ширине.
Отношение подъема задается как отношение величин подъема ступени к ширине проступи в см или мм (рис. 2). В соответствии с этим отношение подъема лестницы 17,8/27,4 означает, что ее ступени имеют высоту подъема 17,8 см и ширину проступи 27,4 см. Для расчета этих величин исходят из средней величины шага человека в 63 см.
Рис. 2. Размеры высот подъема в см, которых следует придерживаться при устройстве лестниц
Размеры ступеней рассчитывают по правилу размера шага :
Лестницы с отношением подъема 17/29 являются наиболее надежными, безопасными и удобными.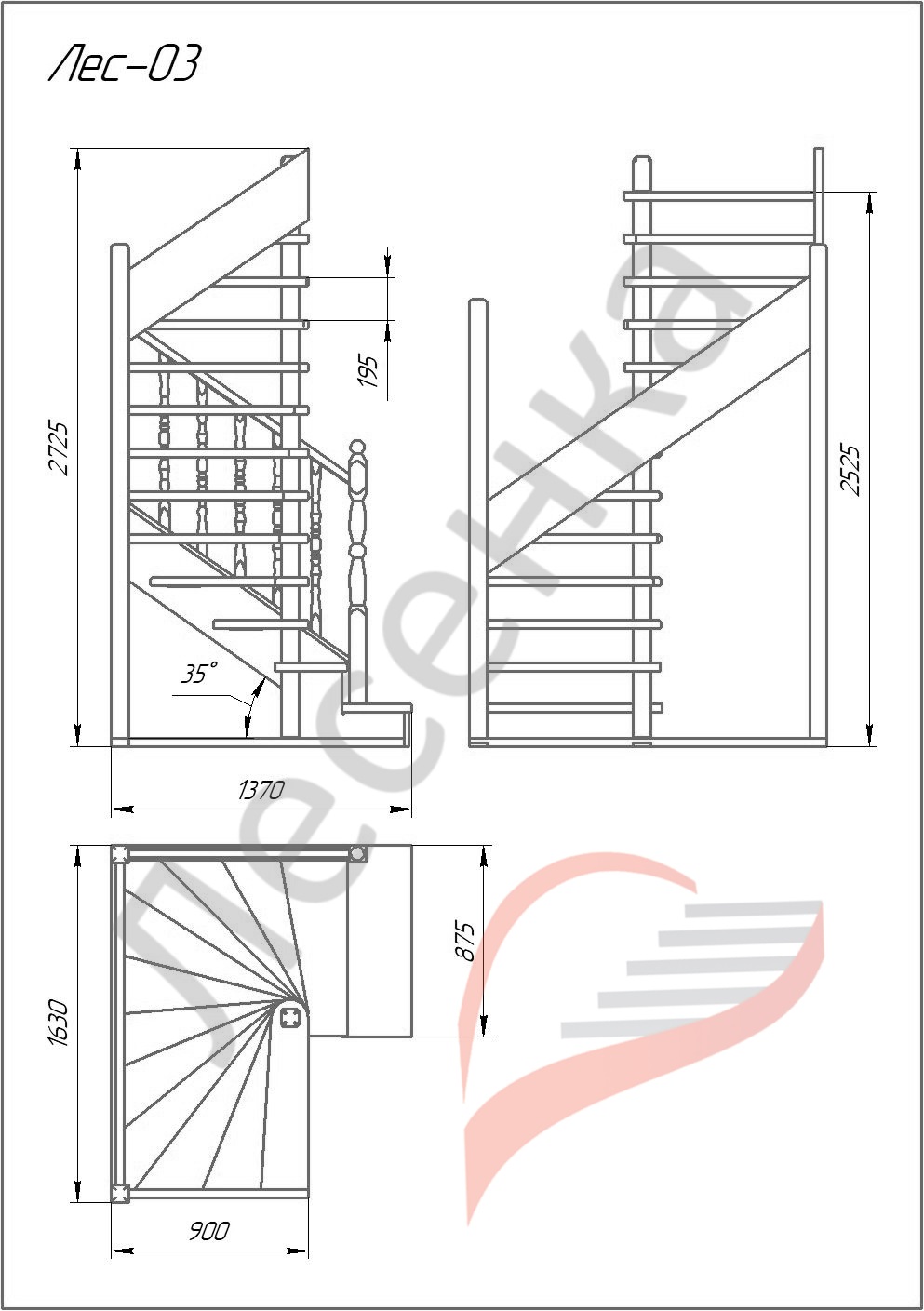
Размеры лестниц
Размеры лестниц определяются с помощью расчета.
Кроме того, необходимо определить ширину лестничного марша и высоту прохода по лестнице.
Расчет лестницы производится в три этапа. Сначала получают высоту подъема ступени s, затем ширину проступи а и затем длину марша лестницы. При этом необходимо иметь в виду, что размеры ступеней внутри одного марша на линии подъема должны быть одинаковыми.
Для расчета отдельных размеров лестницы необходимо учитывать конструкцию пола нижнего и верхнего перекрытий (рис. 3). Расчетные размеры являются готовыми размерами лестницы . Однако для изготовления в первую очередь важны размеры несущей конструкции. Последние можно рассчитать из готовых размеров, вычитая толщину одежды пола.
Рис. 3. План и разрез прямой лестницы
Для определения ширины марша лестниц предписаны минимальные размеры используемой ширины марша (см. рис. 3). Они составляют согласно DIN 18065 для лестниц жилых зданий с не более чем двумя квартирами, не менее 80 см, а свыше двух квартир — 1,00 м. Для ширины лестниц в общественных зданиях, как, например в школах, действуют специальные предписания.
Для ширины лестниц в общественных зданиях, как, например в школах, действуют специальные предписания.
В качестве высоты прохода по лестнице в свету необходимо принимать высоту не менее 2,00 м, для того чтобы проход по лестнице был безопасным. Все лежащие над лестницей строительные конструкции, такие, как перекрытия, балки или лестничные марши, не должны уменьшать высоту прохода по лестнице (см. рис. 3).
Смещение ступеней
У винтовых лестниц в местах закругления образуются клинообразные ступени (рис. 4 и рис. 5). Получение клинообразной формы этих ступеней называют смещением ступеней. Это может быть сделано расчетным или графическим способом.
Рис. 4. Закругленная на четверть лестница
Рис. 5. Наполовину закругленная лестница
Сначала, как и для всех лестниц, определяется количество подъемов п для предусмотренной высоты этажа, а также получающуюся при этом высоту подъема ступени и ширину проступи а. Длина лестницы получается из ширины проступи, умноженной на количество подъемов минус один подъем.
Длина лестницы получается из ширины проступи, умноженной на количество подъемов минус один подъем.
Как производится отделка лестницы ламинатом + обшивка ступенек своими руками
Это необходимо потому, что верхняя проступь совмещается с перекрытием.
На линии подъема длина марша разбивается на соответствующее количество проступей. При этом снова следует учитывать, что верхняя проступь лежит в плоскости перекрытия. При криволинейных лестницах линия подъема в области закругления имеет форму дуги окружности. Средняя точка этой дуги лежит в большинстве случаев в угловой точке внутренних сторон лестницы или совпадает со средней точкой закругления внутренних сторон лестницы. При разбивке линии подъема на проступи следует следить за тем, чтобы угловая ступень по возможности лежала центрально, т.е. чтобы линия, связывающая углы внутренней стороны лестницы и наружные углы лестница примерно делила бы плоскость проступи пополам.
Общие правила по смещению ступеней
- Количество смещаемых ступеней должно быть установлено, потому что его нельзя определить ни расчетным, ни графическим путем.

- Как правило, смещается нечетное количество ступеней, так как угловая ступень должна лежать по центру, совпадая с линией, соединяющей внутренний и внешний углы лестницы (рис. 6).
- Ширина ступеней на внутренней стороне лестницы становится меньше по сравнению с несмещенными ступенями.
- Передняя грань угловой ступени не должна совпадать с линией, соединяющей наружный и внутренний углы.
- Наименьшая ширина проступи не должна быть меньше 10 см.
- С помощью закругления лестницы на внутренней ее стороне размеры проступей можно увеличить.
Рис. 6. Длина угловой ступени и положение центра закругления линии подъема
Смещение у закругленной на четверть лестницы
Процесс при проектировании показан на примере закругленной на четверть лестницы у начала подъема, т.е. при входе на лестницу. Длина линии подъема составляет 3,78 м; отношение подъема лестницы составляет 18/27.
Необходимо сместить ступени со второй по десятую. Решение конструкции производится в три ступени (рис. 7).
Решение конструкции производится в три ступени (рис. 7).
Рис. 7. Смещение ступеней закругленной на четверть лестницы
- В центре лестничного марша вычерчивается линия подъема, на которую наносится полученное количество проступей (1 шаг).
Ширина ступеней на внутренней стороне лестницы определяется графически.
Это производится с помошью вспомогательного построения:
- Конструируется треугольник ABC с прямым углом в вершине А и катетами s.
- s = половине отрезка на внутренней стороне лестницы между смещаемыми ступенями (2 шаг).
- Окружность вокруг А радиусом I разрезает прямую СВ на D.
- I = половине отрезка на линии подъема между смещаемыми ступенями.
- На AD = l наносится ширина проступей смещаемых ступеней.
- Соединительные линии между С и точками деления на / делят АВ = s на искомые ширины ступеней на внутренней стороне лестницы.
- Искомые точки деления переносятся на плане на внутреннюю сторону лестницы.
 Если соединить эти точки деления с соответствующими точками деления на линии подъема, то мы получим соответствующие передние грани ступеней (3 шаг).
Если соединить эти точки деления с соответствующими точками деления на линии подъема, то мы получим соответствующие передние грани ступеней (3 шаг).
Смещение ступеней в закругленной наполовину лестнице
Процесс при проектировании показан на примере закругленной наполовину лестницы. Длина линии подъема составляет 4,05 м; отношение подъема лестницы составляет 18/27.
Должны быть смещены ступени с 3 по 13. Решение конструкции проводится в три ступени (рис. 8).
Рис. 8. Смещение ступеней у наполовину закругленной лестницы
О чем говорят размеры металлочерепицы
Как и любой строительный материал, металлочерепица характеризуется определенными размерами . Ее базовые габариты необходимо учитывать при расчете расхода материалов для кровли. Кроме того этот вид кровельного покрытия отличается разнообразием выбора различных форм профиля, которые во многом определяют визуальный облик и эстетическую привлекательность дома.
Базовые параметры
Полная ширина листа
Это ширина листа, измеряемая от кромки до кромки. Для изготовления металлочерепицы используется холоднокатаная оцинкованная сталь с полимерным покрытием, изготовленная в соответствии с ГОСТ Р 52246—2016. Также полная ширина листа металлочерепицы определяется геометрическими параметрами и глубиной профиля. В большинстве случаев она варьируется в относительно небольших пределах от 1100 до 1200 мм.
Полезная (рабочая) ширина листа.
Ширина листа металлочерепицы , определяемая по разнице полной ширины и нахлеста по ширине. Внахлест листы укладываются при монтаже кровельного покрытия, чтобы оно не пропускало влагу.
Длина листа
В общем случае может варьироваться: компания «Металл Профиль» выпускает металлочерепицу с длиной листа от 500 до 8000 мм. Часто говорят, что идеальная кровля получается в том случае, если длина листа металлочерепицы выбрана равной длине ската. Это действительно минимизирует количество обрезков при монтаже и потребность в крепеже, но работа с листами большой длины имеет определенные особенности и сопряжена с некоторыми рисками, к которым необходимо подготовиться. Прежде всего, следует предусмотреть возможность заезда на площадку длинномерного транспорта и подготовить место для складирования длинных листов металлочерепицы . Также нужно помнить, что их сложнее поднимать наверх и крепить, поэтому понадобится большее число монтажников.
Это действительно минимизирует количество обрезков при монтаже и потребность в крепеже, но работа с листами большой длины имеет определенные особенности и сопряжена с некоторыми рисками, к которым необходимо подготовиться. Прежде всего, следует предусмотреть возможность заезда на площадку длинномерного транспорта и подготовить место для складирования длинных листов металлочерепицы . Также нужно помнить, что их сложнее поднимать наверх и крепить, поэтому понадобится большее число монтажников.
Если людей не хватает, повышаются риски травматизма и повреждения кровельного материала. Наконец, если длинный лист получает повреждения в процессе эксплуатации, то его замена также будет сложнее и дороже. Чтобы сэкономить на обрезках и максимально упростить монтаж, раскладку кровельного покрытия следует предварительно просчитывать. Оценочный расчет по необходимому количеству материалов для кровли вам поможет сделать калькулятора на сайте Компании Металл Профиль.
Но для более точного и предметного расчета стоит обратиться к менеджерам Компании Металл Профиль, которые смогут помочь вам сделать максимально верный просчет, чтобы монтаж проходил с минимальным числом подрезок.
В некоторых случаях можно вообще обойтись набором стандартных длин, которые всегда есть на складе: 0,5; 1,18; 2,25 и 3,65 м. Такой заказ не нужно ждать, как правило, он отгружается день в день.
Профилирование металлочерепицы обусловлено как эстетическими параметрами, от которых зависят внешний вид кровли и его сочетаемость с архитектурой дома, так и эксплуатационными требованиями. В частности, профилированные листы приобретают способность выдерживать снеговые и ветровые нагрузки без деформации. При этом очень важны качество и точность профилирования, поэтому продукция компании «Металл Профиль» производится на самых современных производственных линиях.
Профиль металлочерепицы характеризуется формой и размерами волны:
- Глубина профиля – расстояние от основания до вершины волны;
- Шаг профиля – расстояние между верхними точками соседних волн;
- Высота ступеньки – возвышение каждого следующего ряда волн над предыдущим;
- Длина ступеньки – расстояние между двумя ступеньками.

Чем больше высота профиля и ступеньки, тем более выражен рельеф. А значит, кровля выглядит значительно эффектнее, металлочерепица обладает большей жесткостью и способна удержать и направить потоки воды во время дождя с сильным ветром. Поэтому для протяженных скатов и южных регионов рекомендуется выбирать более рельефную металлочерепицу. Компания «Металл Профиль» выпускает нескольких разновидностей профиля металлочерепицы , отличающиеся различной геометрией. В их числе как распространенные виды, которые сегодня можно встретить у большинства производителей, так и оригинальные разработки.
Наиболее распространенный профиль металлочерепицы с классической формой волны. По некоторым данным, был самым первым, появившимся одновременно с этим видом кровельного покрытия и фактически ставший его синонимом.
- Глубина профиля – 25 мм;
- Шаг профиля – 183,3 мм;
- Высота ступеньки – 14 мм;
- Длина ступеньки – 350 мм;
- Ширина листа – 1190 мм;
- Полезная ширина – 1100 мм.

Размеры металлочерепицы ЛАМОНТЕРРА Х
ЛАМОНТЕРРА с увеличенной до 21 мм высотой ступеньки. Кровельное покрытие становится за счет этого более рельефным и выразительным. ЛАМОНТЕРРА Х с увеличенной до 400 мм длиной ступеньки. Такая геометрия делает рельеф кровельного покрытия более всего похожим на рельеф классической глиняной черепицы. Оригинальный профиль, отличающийся строгими геометрическими формами и прямым ровным рисунком, благодаря чему он напоминает плитку шоколада. Подчеркнет индивидуальность и подойдет домам как в классическом стиле, так и в стиле Hi Tech. Металлочерепица Каскад имеет целых двадцать ребер жесткости, что делает ее чрезвычайно устойчивой к снеговым нагрузкам и оптимальной для применения в северных регионах, Сибири и т.д.
- Глубина профиля – 22,5 мм;
- Шаг профиля – 274 мм;
- Высота ступеньки – 22,5 мм;
- Длина ступеньки – 350 мм;
- Ширина листа – 1180 мм;
- Полезная ширина – 1120 мм.

Размеры металлочерепицы МОНТЕРРОСА
Этот профиль своим названием обязан эксклюзивной форме волны, геометрия которой напоминает рельеф горного массива. Придает кровле особую выразительность и выделяет дом на фоне других построек. Большой выбор вариантов сочетания длины и высоты ступеньки позволяет подобрать наиболее привлекательную конфигурацию и добавить дому индивидуальности. В процессе производства листов используется технология 3D-реза, благодаря чему после монтажа горизонтальные стыки становятся практически незаметны. Двойная капиллярная канавка обеспечивает герметичность вертикального нахлеста. Особая геометрия продольного нахлеста позволяет использовать материал без лишнего металла в замке и минимизировать количество обрезков. Выпускается с полимерными покрытиями класса «премиум» и «премьер».
- Глубина профиля – 42 мм;
- Шаг профиля – 277,5 мм;
- Высота ступеньки – 25, 30 или 35 мм;
- Длина ступеньки – 350 или 400 мм;
- Ширина листа – 1170 мм;
- Полезная ширина – 1110 мм.

Размеры металлочерепицы МОНТЕКРИСТО
Оригинальный симметричный профиль, который невозможно спутать ни с каким другим. Как и Монтерроса, отличается вариативностью сочетания длины и высоты ступеньки. Обрезная кромка по контуру волны делает металлочерепицу Монтекристо похожей на глиняную, но при этом она гораздо более выразительная, чем различные варианты стандартного ЛАМОНТЕРРА. Сочетание скруглённых форм и прямых линий прекрасно гармонирует со множеством архитектурных стилей и дизайнерских решений.
- Глубина профиля – 24 мм;
- Шаг профиля – 230 мм;
- Высота ступеньки – 25, 30 или 35 мм;
- Длина ступеньки – 350 или 400 мм;
- Ширина листа – 1200 мм;
- Полезная ширина – 1150 мм.
Размеры металлочерепицы ТРАМОНТАНА
Еще одно оригинальное кровельное покрытие Компании Металл Профиль с несколькими вариантами высоты ступеньки. Усиленный профиль металлочерепицы Трамонтана делает ее особо устойчивой к ветровым нагрузкам, включая порывистые и ураганные ветры.
- Глубина профиля – 25 мм;
- Шаг профиля – 230 мм;
- Высота ступеньки – 25, 30 или 35 мм;
- Длина ступеньки – 350 или 400 мм;
- Ширина листа – 1195 мм;
- Полезная ширина – 1155 мм.
Лестница в доме на второй этаж (формы, размеры, материалы).
Лестница в доме имеет прямую зависимость от площади нашего помещения. В соответствии с этим мы планируем лестничную конструкцию возможной формы, размера и используемого материала.
Дизайнеры и конструкторы позаботились о нас и предлагают лестницы довольно обширного разнообразия форм. Здесь можно выделить: маршевые, винтовые и смешанные подъемные механизмы.
Среди маршевых лестниц встречаются такие формы: прямая, Г-образная
П-образная, Т-образная, трапециевидная. Прямая лестница состоит из одного прямого марша ступеней и располагается у стены, либо в центре помещения. Лестницы состоящие из нескольких маршей разделяются поворотными площадками.
Маршевые лестницы наиболее удобны и безопасны в использовании. По этому признаку их чаще всего монтируют в частных домах. Но обязательно нужно учитывать, что двухмаршевые и более лестницы занимают довольно много пространства. И подходят для домов большой площади.
Лестницы с забежными ступенями похожие по форме на маршевые, но не имеющие поворотных площадок. Вместо площадок у таких лестниц располагают поворотные ступеньки. Что позволяет экономить место в доме.
Форма винтовых лестниц скрывается в самом названии. Они имеют конструкцию подъема в виде винта. Основу для таких лестниц берет на себя опорный столб — металлическая основательная конструкция в центре, вокруг которой крепятся забежные ступени огражденные с наружней стороны перилами.
Винтовые лестницы обычно занимают не так много места их можно располагать в любом месте помещения. Но чем уже их диаметр тем не безопаснее по нем ходить. Ступени становятся короче, а в виду своей неправильной формы и уже.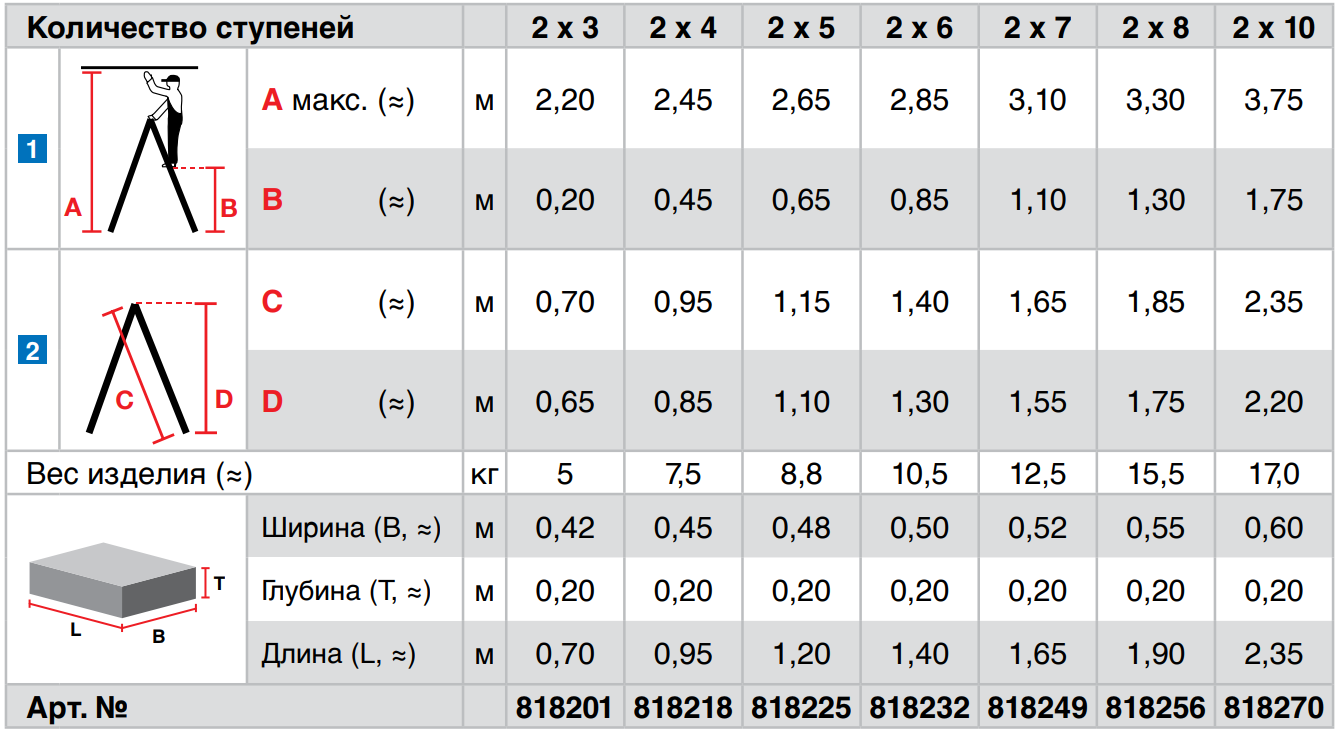
Поэтому передвигаться по такой конструкции нужно предельно внимательно. Винтовые лестницы используются в домах с небольшой площадью, либо в просторных помещениях используя большие размеры ступеней и оригинальный дизайн.
Еще одно интересное решение это спиралевидные лестницы. Когда опорный столб расширяют либо совсем не устанавливают, то конструкция больше напоминает спираль.Такую форму лестницы можно расположить в большом просторном холле дома и сделать ее центром вашего дизайн проекта дома. За счет увеличения диаметра спиральная конструкция становится более удобной в эксплуатации.
Встречаются также лестницы со смешанными формами подъемных механизмов. Нередко используют маршевые лестницы без площадок использую забежные ступени, располагая конструкцию лестницы в углу дома. Это существенно экономит место в помещении.
Строительство лестницы в доме предполагает ряд размерных стандартов для безопасности и долговечности конструкции. Стоит выделить основные моменты размеров для ступеней и ограждений.
Чтобы уверенно подниматься и спускаться по лестнице обязательно должна быть правильно выбрана ширина и высота ступеней.
Существуют некоторые стандарты, которых необходимо придерживаться.
- Длина ступеней в частном доме соответствует ширине лестничного марша и составляет от 70 до 120 см. Чем длиннее будет это расстояние тем комфортнее будет находиться на лестнице двум людям. А также появится возможность для спуска и подъема мебели.
- Глубина ступени (проступи) составляет 25-30 см. Она зависит от средней длины ступни человека.
- Для стандартных конструкций высота подступенка может составлять примерно от 12 до 22 см.
Глубину ступеньки (проступи) можно определить таким способом: встаньте на ступеньку, если носок обуви будет выступать над краем на 1 см, значит, ширина подобрана правильно. Если на 1,5 см и более – такая лестница считается небезопасной.
Можно воспользоваться таблицей соотношения размеров ступеней.
| Размер ступеней, мм | Угол наклона марша | |
| Ширина | Высота | |
| 400 | 100 | 14° 10´ |
| 380 | 110 | 16° 20´ |
| 360 | 120 | 18° 30´ |
| 340 | 130 | 21° 00´ |
| 320 | 140 | 23° 10´ |
| 300 | 150 | 26° 40´ |
| 280 | 160 | 29° 50´ |
| 260 | 170 | 33° 10´ |
| 240 | 180 | 37° 00´ |
| 220 | 190 | 40° 50´ |
| 200 | 200 | 45° 00´ |
При подъеме по лестнице мы интуитивно пытаемся ухватиться за перила.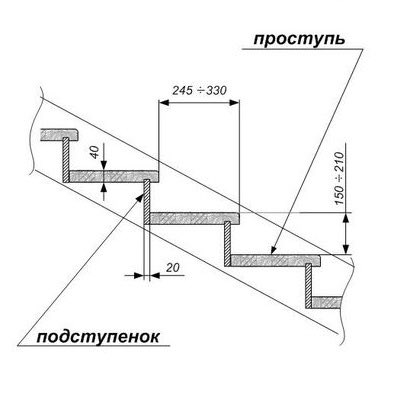 Опора придает нам чувство безопасности. Поэтому лестницу принято оборудовать ограждениями и перилами.
Опора придает нам чувство безопасности. Поэтому лестницу принято оборудовать ограждениями и перилами.
По правилам конструкцию имеющую более трех ступеней нужно оборудовать ограждением. Важно учитывать правильные размеры перил согласно Госту.
- Перила деревянной лестницы в жилом строении не должны быть ниже, чем 90 см.
- Размер ограждения лестничной площадки и площадки для входа на лестницу, ведущую на чердак, не должен быть меньше 90 см.
- Высота ограждений на наружной лестнице не должна быть меньше 120 см.
- В помещениях, где постоянно находятся дети перила не должны быть ниже, чем 118 см.
Соблюдая эти требования вы будете комфортно и безопасно чувствовать себя при подъеме или спуске держась за перила. Общепринятая нагрузка, которую должны выдерживать перила 30 кг/см². В конструкции перил на лестницах, где проживают дети маленького возраста, должны отсутствовать горизонтальные и наклонные элементы заполнения.
Если с конструкцией размерами лестницы вы уже определились, то остается вопрос из какого материала ее сделать? Выбирать материал стоит отталкиваясь от вашего предпочтения, финансовых возможностей, а также и стилевого решения всего помещения в целом.
Лестницы в дом изготавливают из дерева, металла, с использованием различных комбинаций материалов. Могут быть выбраны такие основания лестниц как дерево, бетон и металл. А отделку возможно произвести комбинируя, например ступени деревянные или каменные, а ограждения металлические или стеклянные.
При выборе камня или плитки для облицовки ступеней, используем материал текстуры которая не будет скользить при эксплуатации. Дабы избежать падений на лестнице. Лучшим вариантом при отделке ступеней выступает дерево. Оно дешевле, подлежит любому виду окраски, приятное и теплое на ощупь. Можно без боязни ступать босиком.
Для изготовления ограждений лестницы дерево также смотрится выигрышно и может принимать любую форму. Будь то простая и лаконичная или же резная и витиеватая. Прекрасно смотрятся резные балясины, а заходным столбам можно придать форму фигур животных, птиц или силуэтов.
Современный дизайн предлагает оборудовать лестницу из металла с сочетанием стекла. Такой стиль визуально расширяет пространство, и придает воздушности помещению.
Такой стиль визуально расширяет пространство, и придает воздушности помещению.
И так, чтобы сделать лестницу на второй этаж в своем доме, выбирайте форму по вашему пожеланию и площади помещения. Не забываем учитывать правильные размеры ступеней и ограждений, чтобы не испытывать дискомфорта при подъемах и спусках, а также избежать падений. Материал для лестницы зависит от ваших предпочтений и веяний моды. Выбирайте материал с которым вам приятнее соприкасаться, ведь по лестнице придется ходить не один раз на день.
границ | Адаптивное управление размером шага расширенного/неароматизированного фильтра Калмана с использованием концепции обработки событий
1. Введение и определение проблемы
Контроль размера шага обычно содержит процедуру обработки событий для определения момента времени конкретного события. Обработка событий и обнаружение пересечения нуля являются хорошо известными и хорошо зарекомендовавшими себя подходами к численному моделированию (Watts, 1984; Zhang et al. , 2008). Идея повышения производительности за счет определения момента времени, в который происходят события, известна в области решателей ОДУ.В Esposito and Kumar (2007) представлен алгоритм обнаружения событий для негладких дифференциальных уравнений. В этой статье полином экстраполяции используется для выбора размера шага интегрирования для обнаружения возможных будущих событий. Этот подход имеет преимущества, особенно вблизи особенностей модели, где производная функция не определена в пространстве состояний. Сингулярные системы можно моделировать как марковские скачкообразные сингулярные системы. Исследование устойчивости, стабилизация, управление и фильтрация этих систем более сложны по сравнению с системами, моделируемыми в пространстве состояний (Wang et al., 2017).
, 2008). Идея повышения производительности за счет определения момента времени, в который происходят события, известна в области решателей ОДУ.В Esposito and Kumar (2007) представлен алгоритм обнаружения событий для негладких дифференциальных уравнений. В этой статье полином экстраполяции используется для выбора размера шага интегрирования для обнаружения возможных будущих событий. Этот подход имеет преимущества, особенно вблизи особенностей модели, где производная функция не определена в пространстве состояний. Сингулярные системы можно моделировать как марковские скачкообразные сингулярные системы. Исследование устойчивости, стабилизация, управление и фильтрация этих систем более сложны по сравнению с системами, моделируемыми в пространстве состояний (Wang et al., 2017).
В Бернале (1991) автор обратился к расчету размеров временного шага для предотвращения межшаговых событий в полилинейных задачах. В данной работе представлен подход для локализации момента времени, когда жесткость изменяется в нелинейной системе..jpg) Этот подход можно рассматривать как схему интерполяции времени, когда происходят события, используя вычисленные отклики в конце соответствующего линейного шага. В Wright and Pei (2012) предлагается явный численный метод для решения дифференциально-алгебраических уравнений (ДАУ) с учетом разрывов низкого порядка в алгебраических уравнениях восстанавливающей силы.Эффективность этого подхода проверена для конкретного класса задач, а именно негладких ДАУ с разрывами. Алгоритм способен автоматически определять местоположение каждого события состояния.
Этот подход можно рассматривать как схему интерполяции времени, когда происходят события, используя вычисленные отклики в конце соответствующего линейного шага. В Wright and Pei (2012) предлагается явный численный метод для решения дифференциально-алгебраических уравнений (ДАУ) с учетом разрывов низкого порядка в алгебраических уравнениях восстанавливающей силы.Эффективность этого подхода проверена для конкретного класса задач, а именно негладких ДАУ с разрывами. Алгоритм способен автоматически определять местоположение каждого события состояния.
В реальности динамика системы моделируется линейными или нелинейными обыкновенными дифференциальными уравнениями. Например, в Bakhshande and Söffker (2015) упругая балка моделируется как линейное ОДУ. Пропорционально-интегральный наблюдатель (PIO) с высоким коэффициентом усиления, представленный Söffker et al. (1995) используется для оценки перемещений узлов упругой балочной системы, а также влияния возмущающей силы на динамику системы. Динамика системы и наблюдателя дополняется и описывается в одной линейной форме ОДУ. Вышеупомянутый пример может быть описан подходящей начальной задачей (IVP). В этом случае используются жесткие решатели, способные решать жесткие задачи, чтобы избежать большого времени вычислений за счет уменьшения размера шага интегрирования, когда нет быстрых изменений в состояниях системы и динамике возмущений, а также для улучшения результатов оценки за счет уменьшения размера шага интегрирования в случай быстрого динамического поведения, связанного с возмущениями (жесткое поведение).В Bakhshande and Söffker (2015) результаты моделирования получены с использованием жесткого решателя ОДУ в Matlab (ode15s) с учетом обработки событий и процедур пересечения нуля.
Динамика системы и наблюдателя дополняется и описывается в одной линейной форме ОДУ. Вышеупомянутый пример может быть описан подходящей начальной задачей (IVP). В этом случае используются жесткие решатели, способные решать жесткие задачи, чтобы избежать большого времени вычислений за счет уменьшения размера шага интегрирования, когда нет быстрых изменений в состояниях системы и динамике возмущений, а также для улучшения результатов оценки за счет уменьшения размера шага интегрирования в случай быстрого динамического поведения, связанного с возмущениями (жесткое поведение).В Bakhshande and Söffker (2015) результаты моделирования получены с использованием жесткого решателя ОДУ в Matlab (ode15s) с учетом обработки событий и процедур пересечения нуля.
и его расширения (EKF и UKF) имеют те же функции, что и наблюдатели для прерывистых систем и измерений, содержащих статистический шум и другие неточности. Были внедрены различные подходы для улучшения характеристик KF и EKF/UKF. Например, итерационный расширенный фильтр Калмана (IEKF) (Bell and Cathey, 1993) итеративно линеаризует нелинейные уравнения системы, чтобы компенсировать значительные нелинейности.В данном алгоритме рассматривается итерационная процедура обновления измерений (корректирующая часть). Итерационная процедура останавливается, если достигнуто максимальное количество итераций или разница между результатами двух итераций меньше заранее заданного порога. В Skoglund et al. (2015), предполагая, что EKF является задачей оптимизации, считается, что различные алгоритмы оптимизации (например, линейный поиск, квази-Ньютон и Левенберг-Марквардт) улучшают производительность и надежность оценки.В Havlík and Straka (2015) представлен итерированный расширенный фильтр Калмана с переменной длиной шага. В этом подходе время расчета рассматривается как фиксированное значение. Шаг обновления измерения рассчитывается на основе алгоритма Гаусса-Ньютона или процедуры оптимизации линейного поиска с переменной длиной шага.
Например, итерационный расширенный фильтр Калмана (IEKF) (Bell and Cathey, 1993) итеративно линеаризует нелинейные уравнения системы, чтобы компенсировать значительные нелинейности.В данном алгоритме рассматривается итерационная процедура обновления измерений (корректирующая часть). Итерационная процедура останавливается, если достигнуто максимальное количество итераций или разница между результатами двух итераций меньше заранее заданного порога. В Skoglund et al. (2015), предполагая, что EKF является задачей оптимизации, считается, что различные алгоритмы оптимизации (например, линейный поиск, квази-Ньютон и Левенберг-Марквардт) улучшают производительность и надежность оценки.В Havlík and Straka (2015) представлен итерированный расширенный фильтр Калмана с переменной длиной шага. В этом подходе время расчета рассматривается как фиксированное значение. Шаг обновления измерения рассчитывается на основе алгоритма Гаусса-Ньютона или процедуры оптимизации линейного поиска с переменной длиной шага.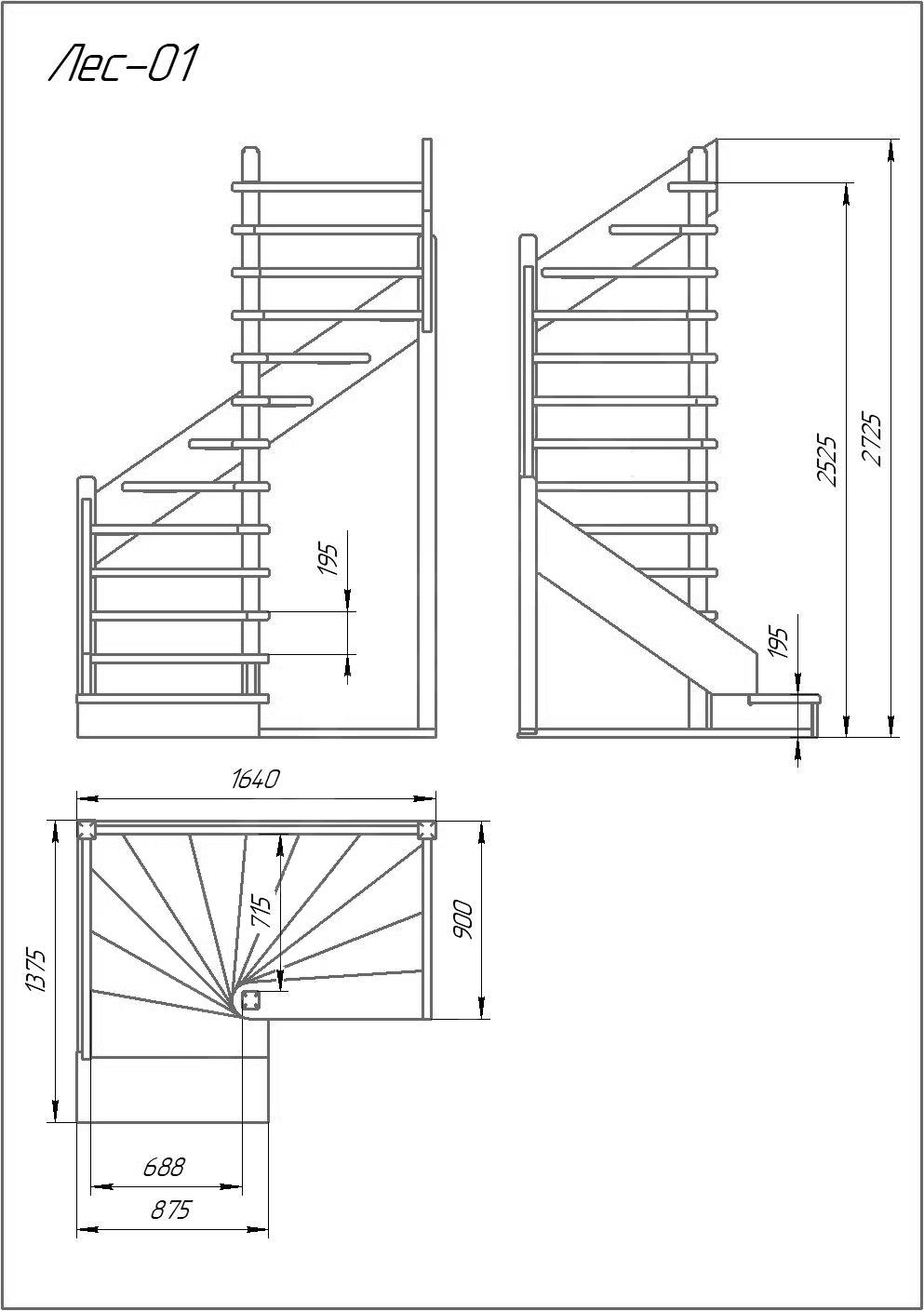 Здесь размер шага рассматривается как размер шага процедуры оптимизации для обеспечения сходимости заранее определенных критериев.
Здесь размер шага рассматривается как размер шага процедуры оптимизации для обеспечения сходимости заранее определенных критериев.
В Wang and Li (2008) предлагается основанный на событиях наблюдатель с фильтром Калмана для управления угловым положением поворотного высокоскоростного двухпозиционного клапана.Измерения, полученные в нерегулярные моменты времени и обнаруженные энкодером. Неопределенность времени возникновения переходного события рассматривается как нулевой средний случайный шум измерения, воздействующий на положение вращения. Этот шум измерений, на который влияет время дискретизации, рассматривается как часть модели системы, используемой для оценки фильтра Калмана. В Chatzis and Chatzi (2017) прерывистый фильтр Калмана без запаха (DUKF) предлагается в качестве модифицированной версии UKF. Этот подход адаптирует формулировку пространства состояний, оценивает наблюдаемость на каждом временном шаге и выбирает подходящее подпространство, которое может использоваться UKF.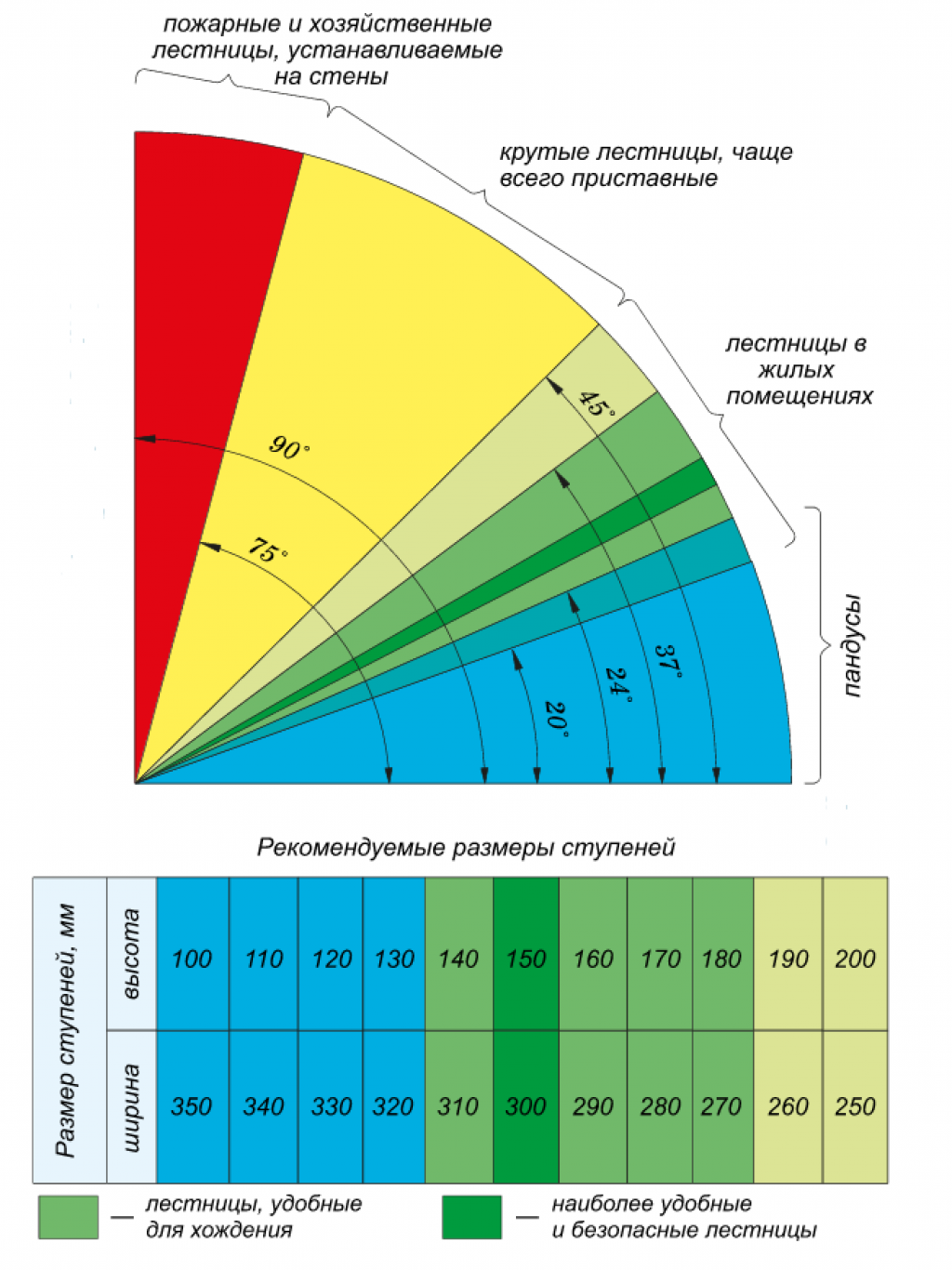 Следовательно, неидентифицируемые параметры (связанные с негладким поведением) обнаруживаются и исключаются из постановки задачи.
Следовательно, неидентифицируемые параметры (связанные с негладким поведением) обнаруживаются и исключаются из постановки задачи.
Непрерывный дискретный фильтр Калмана, запускаемый событием, представлен в Niu et al. (2018). СКО оценки управляется путем обнаружения события и проведения нового измерения. Этот подход уменьшает шаг расчета на каждом шаге, чтобы достичь желаемой ошибки оценки в текущем шаге расчета. Следующая оценка начинается с повторной инициализации шага расчета к исходному.
Во всех вышеупомянутых подходах шаг расчета результатов оценивания определяется постоянным (на основе измерений) или просто уменьшается на текущем шаге и повторно инициализируется для следующего временного шага. Цель состоит в том, чтобы достичь подходящей производительности оценки (в случае события). Ни один из упомянутых подходов не фокусируется на управлении временем расчета с учетом обнаружения событий путем увеличения и уменьшения времени расчета во время процедуры оценки (например, решатели ОДУ). В этом вкладе шаг расчета управляется на основе производительности оценки.Она уменьшается в том случае, если ошибка оценки увеличивается для достижения желаемой производительности. Соответственно, он увеличивается, когда производительность достаточно подходит для уменьшения вычислительных усилий.
В этом вкладе шаг расчета управляется на основе производительности оценки.Она уменьшается в том случае, если ошибка оценки увеличивается для достижения желаемой производительности. Соответственно, он увеличивается, когда производительность достаточно подходит для уменьшения вычислительных усилий.
Процедуры обработки событий и перехода через нуль использовались и улучшались по сравнению с предыдущими годами для решения жестких ОДУ. Основная цель этой статьи состоит в том, чтобы интегрировать преимущества обработки событий и процедур пересечения нуля в схему дискретного предиктора-корректора расширенного/без запаха фильтра Калмана для адаптивного управления размером шага.Процедура ФК начинается с начального набора параметров Калмана и состояний системы. Следующий шаг оценки реализуется на основе информации о текущем шаге (та же концепция, что и для IVP). Обычно подходы «предиктор-корректор» основаны на заранее заданном допуске. Чтобы использовать KF для задач переключения/жесткости, алгоритм должен иметь возможность оглянуться назад, выполнить решение с меньшим размером шага (жесткие задачи), выполнить решение в точно определенные моменты времени (задачи переключения) и достичь предопределенного допуска. Таким образом, в этом вкладе предлагается новый расширенный/без запаха фильтр Калмана путем расширения управления переменным размером шага в схеме предиктор-корректор для жестких/переключающих систем. Предлагаемый расширенный/без запаха фильтр Калмана с переменным размером шага способен решить оценку состояния жестких задач за дискретное время, чтобы избежать ненужной высокой вычислительной нагрузки, если это необходимо, и повысить производительность оценки. Использование предложенного расширенного/неароматизированного фильтра Калмана с переменным размером шага позволяет контролировать размер шага внутри процедуры предиктор-корректор.Время выборки адаптируется на основе текущей производительности оценки (инновация EKF/UKF) состояний системы.
Таким образом, в этом вкладе предлагается новый расширенный/без запаха фильтр Калмана путем расширения управления переменным размером шага в схеме предиктор-корректор для жестких/переключающих систем. Предлагаемый расширенный/без запаха фильтр Калмана с переменным размером шага способен решить оценку состояния жестких задач за дискретное время, чтобы избежать ненужной высокой вычислительной нагрузки, если это необходимо, и повысить производительность оценки. Использование предложенного расширенного/неароматизированного фильтра Калмана с переменным размером шага позволяет контролировать размер шага внутри процедуры предиктор-корректор.Время выборки адаптируется на основе текущей производительности оценки (инновация EKF/UKF) состояний системы.
Этот вклад основан на ранее опубликованной первоначальной исследовательской статье (Bakhshande and Söffker, 2018). В Bakhshande and Söffker (2018) представлена первая идея для линейных систем и, соответственно, фильтра Калмана. Дополняя и детализируя первоначальную работу, в этом вкладе предлагается расширенная и улучшенная версия управления размером шага для нелинейного динамического поведения с учетом EKF и UKF. Кроме того, в этом вкладе исследуется корректировка проектных параметров, чтобы получить подходящую скорость сходимости и ошибку оценки.
Кроме того, в этом вкладе исследуется корректировка проектных параметров, чтобы получить подходящую скорость сходимости и ошибку оценки.
используется здесь как нелинейный дискретный фильтр, который можно заменить любым другим дискретным фильтром для линейных или нелинейных систем. Основные вклады этой статьи можно резюмировать следующим образом:
• Представлен новый дискретный EKF/UKF, запускаемый событием, для жестких/переключаемых нелинейных систем, основанный на процедуре обработки событий в решателях ODE.
• Адаптация временного шага в EKF/UKF (дискретный мир) на основе нововведения Калмана как ключевой вклад этой статьи (управление размером шага в дискретном мире).
• Управление нововведением ошибки оценки для EKF/UKF и вычислительных усилий при определяемых пороговых значениях (α и β).
Статья организована следующим образом: сначала дается общее определение жестких/коммутационных систем, помимо общих решений для решения жестких ОДУ.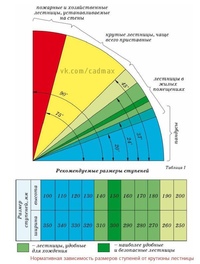 Во второй части представлены основные аспекты (на базе Matlab) решателей ОДУ, например.g., процедуры пересечения нуля и обработки событий с целью интеграции в структуру расширенного/без запаха фильтра Калмана. Впоследствии предлагаемый расширенный/без запаха фильтр Калмана с переменным размером шага детализируется с учетом структуры и процедуры хорошо известного дискретного EKF/UKF. Кроме того, предлагаемый метод оценивается с использованием результатов моделирования осциллятора Ван-дер-Поля (общий пример переключающей/жесткой системы). Последний раздел завершает статью кратким изложением и выводами.
Во второй части представлены основные аспекты (на базе Matlab) решателей ОДУ, например.g., процедуры пересечения нуля и обработки событий с целью интеграции в структуру расширенного/без запаха фильтра Калмана. Впоследствии предлагаемый расширенный/без запаха фильтр Калмана с переменным размером шага детализируется с учетом структуры и процедуры хорошо известного дискретного EKF/UKF. Кроме того, предлагаемый метод оценивается с использованием результатов моделирования осциллятора Ван-дер-Поля (общий пример переключающей/жесткой системы). Последний раздел завершает статью кратким изложением и выводами.
2. Жесткая/система переключения
Обыкновенное дифференциальное уравнение (ОДУ) содержит производную(ые) зависимой переменной (обычно обозначаемой как x и соответствующую производную(ые) как х , х , …) по отношению к одной независимой переменной (обычно обозначающей ко времени т ). Задачи начального значения (IVP) решаются итеративно, принимая начальное условие x ( t 0 ) = x 0 и интересующий период времени t = [ 90 7 4 8 t , т ф ]. На каждом шаге решатель использует результаты предыдущего шага с учетом конкретного алгоритма (метод Эйлера, методы Рунге-Кутты и т. д.). Окончательный результат задается в виде вектора шагов по времени t = [ t 0 , t 1 , …, t f 9004 для соответствующей последовательности значений переменной x = [ x 0 , x 1 , …, x f ].Дифференциальные уравнения высших порядков могут быть переформулированы на каждом шаге итерационной процедуры решения ИВП в виде системы уравнений первого порядка:
На каждом шаге решатель использует результаты предыдущего шага с учетом конкретного алгоритма (метод Эйлера, методы Рунге-Кутты и т. д.). Окончательный результат задается в виде вектора шагов по времени t = [ t 0 , t 1 , …, t f 9004 для соответствующей последовательности значений переменной x = [ x 0 , x 1 , …, x f ].Дифференциальные уравнения высших порядков могут быть переформулированы на каждом шаге итерационной процедуры решения ИВП в виде системы уравнений первого порядка:
с размером шага:
и соответствующее решение:
х(tn+1)=x(tn)+∫tntn+1f(τ,x(τ))dτ. (3) Обычно, даже если функция f является непрерывной функцией, нет гарантии, что IVP обеспечивает уникальное решение. Принимая во внимание теорему Пикара согласно Зюли (2001) и условие Липшица для функции f , можно утверждать, что для уравнения (1) существует единственное решение.
В Atkinson et al. (2011) линейное приближение общего ОДУ (уравнение 1) вводится как:
х.(t)=Ax+g(t), (4)с A = F = F = x ( T ( T 0 , x 0 ) Как м × м Jacobian Matrix F оценивается в ( T 0 , x 0 ).
Определение 1. [Согласно Хайреру и Ваннеру (1987)]: Система ẋ ( t ) = f ( t, x ( t ) называется сепарабельно жесткой ) Position ( T 0 , x , x 0 ) Если jacobian j = ∂f∂x (t0, x0) обладает k < n eigenvalues λ 1 , λ 2 , …, λ k такой, что
мин|λi|1≤i≤k>>max|λi|k+1≤i≤n.(5)Собственные значения λ 1 , λ 2 , …, λ k называются жесткими собственными значениями и,
μ=min|λi|1≤i≤k/max|λi|k+1≤i≤n, (6) относительное расстояние .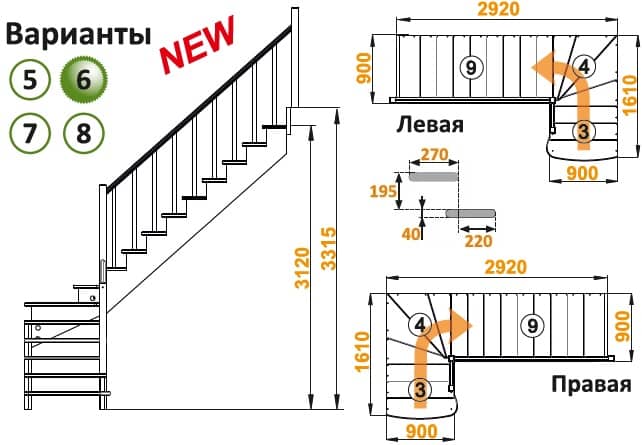
Уравнения жесткой/переключаемой системы содержат некоторые члены, которые приводят к быстрому изменению решения. Согласно Хайреру и Ваннеру (1987), относительное разделение может определять уровень жесткости. Другими словами, собственное значение, отвечающее за самые медленные скорости изменений, следует сравнивать с теми, которые приводят к самым быстрым изменениям.
При рассмотрении нелинейных систем сложность возрастает, поскольку в этом случае жесткость становится глобальным свойством и, следовательно, не может быть сведена к локальной задаче путем использования решения в окрестности отдельных точек. Нелинейная задача может начаться с нежесткого поведения и стать жестким, или наоборот. Он может содержать жесткие и нежесткие интервалы. В Ашино и соавт. (2000) вводится следующее всеобъемлющее определение жесткой системы для линейных и нелинейных систем.
Определение 2. Если численный метод вынужден использовать на определенном интервале интегрирования длину шага, чрезмерно малую по сравнению с гладкостью точного решения на этом интервале, то говорят, что задача жесткая в этом интервале .
Для решения численного интегрирования жесткого обыкновенного дифференциала (уравнение 1) требуется подходящий небольшой размер шага h n в случае быстрого изменения решения, и, соответственно, размер шага должен быть относительно большим (расслабленным ), когда решение гладкое.Следовательно, идеальное численное решение способно решать жесткие и нежесткие ОДУ, обозначаемые как контроль размера шага (Watts, 1984). Жесткие численные методы имеют возможность изменять размер шага в процессе решения. Они предпринимают небольшие шаги для получения удовлетворительных результатов рядом с решениями, которые быстро меняются. Основным преимуществом жестких решателей является малое время вычислений по сравнению с нежесткими решателями. Нежесткие решения могут использоваться для жестких задач с надлежащим малым размером шага, но для достижения окончательного решения требуется больше времени, поскольку размер шага постоянен и не может быть адаптирован в соответствии с фактическими результатами.
3. Пересечение нуля и процедуры обработки событий
В этом разделе повторяются основные идеи пересечения нуля и обработки событий, которые можно будет использовать позже, представляя предлагаемый алгоритм. Здесь они кратко повторяются, поскольку именно эти идеи будут перенесены в конечно-разностную схему расчета цифровых фильтров типа фильтра Калмана.
Как обсуждалось в разделе 1, решатели с переменным размером шага увеличивают или уменьшают размер шага для достижения допусков на ошибки и требуемой или заданной производительности.Выбор фиксированного или переменного размера шага зависит от динамической модели и проблем реализации. Решатель с фиксированным размером шага использует один размер шага для всего времени моделирования, и, следовательно, размер шага должен быть достаточно мал, чтобы соответствовать требованиям точности.
Неявные решатели с переменным размером шага (жесткие решатели) могут использоваться для решения жестких задач. Нежесткие решатели неэффективны на интервалах, где решение меняется медленно, потому что они используют временные шаги, достаточно малые, чтобы разрешить максимально быстрое изменение за все время оценки. Кроме того, размер шага нежестких решателей должен быть определен на уровне инициализации и не может быть изменен во время процедуры решения.
Кроме того, размер шага нежестких решателей должен быть определен на уровне инициализации и не может быть изменен во время процедуры решения.
Процедуры обработки событий и пересечения нуля обычно учитываются в решателях ОДУ. Определение момента времени конкретных событий в ОДУ относится к процедуре обработки событий. Например, точное время, когда мяч падает на землю, или время, когда решения ОДУ достигают определенного значения, — это очень конкретный момент. Событие обнаруживается с временного шага t n до t n +1 , если условие (событие) становится истинным.Алгоритм обнаружения пересечения нуля представляет собой процедуру точного захвата и определения местоположения событий. В случае пересечения нуля для предопределенного события решатель ОДУ может быть остановлен или продолжен с другими условиями в зависимости от потребности. Обнаружение событий решателей ОДУ содержит две функции f ( t, x ) и g ( t, x ) и начальное условие ( t 0 , x 8 090).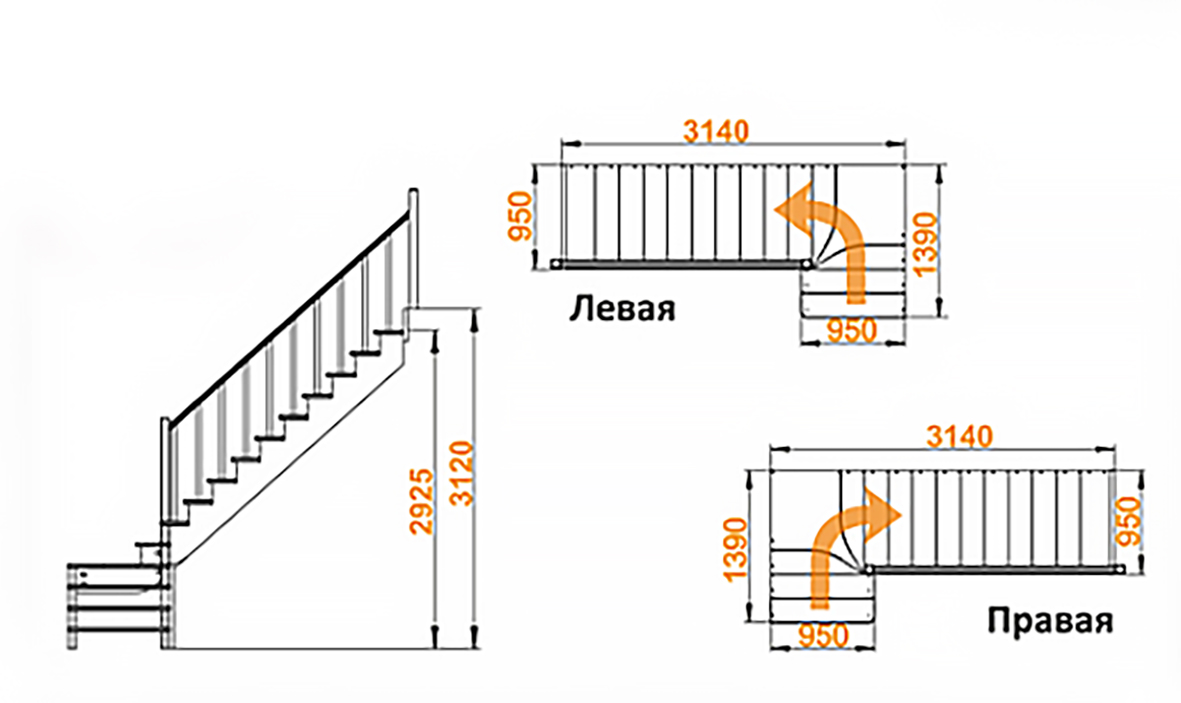 Использование процедуры обработки событий в структуре решателя ОДУ означает численно определить момент времени t * так, чтобы:
Использование процедуры обработки событий в структуре решателя ОДУ означает численно определить момент времени t * так, чтобы:
Здесь г ( t, x ) обозначает условие события, которое должно быть определено программистом в соответствии с требованиями.
4. Фильтр Калмана с расширенным/без запаха
Фильтрация является важной и фундаментальной проблемой в области управления с дискретным временем. Например, в Wang et al. (2019) нечеткий фильтр предназначен для нечетких дескрипторных систем с дискретным временем с учетом ограниченного количества ненадежных каналов связи.Одной из наиболее важных фильтрующих структур в области управления является фильтр Калмана. В принципе, фильтр Калмана можно использовать (i) для оценки состояния системы, когда его нельзя измерить напрямую, или (ii) для объединения информации датчиков, когда измерения доступны с разных датчиков, но могут быть подвержены шуму. Хотя для этого фильтра можно рассмотреть множество приложений, это две наиболее важные задачи и приложения этого фильтра.
Хотя для этого фильтра можно рассмотреть множество приложений, это две наиболее важные задачи и приложения этого фильтра.
Основная цель этого фильтра — получить окончательную оценку с нулевым смещением и минимальной дисперсией по сравнению с реальным значением и с учетом зашумленных измерений.Фильтр Калмана является оптимальным линейным фильтром в смысле минимизации оценки дисперсии состояний при допущении, что модель системы полностью соответствует реальной системе, входящий шум является белым (некоррелированным) и ковариации шума точно известны (Андерсон и Мур, 2012). Другими словами, для систем, отвечающих требованиям, KF — лучший выбор. Фильтр Калмана впервые был представлен Калманом (1960) для формулировки и решения задачи фильтра Винера, которая подходит для фильтрации, сглаживания и прогнозирования стационарных сигналов в широком смысле.Стоит отметить, что фильтр Калмана в дискретной или непрерывной форме и его расширения (Bishop and Welch, 2001) представлены как фундаментальный алгоритм для решения широкого круга задач оценивания.
Расширенный фильтр Калмана (EKF) был введен для нелинейных систем путем линеаризации оценки вокруг текущей оценки и использования частных производных уравнения системы/измерения (Sorenson, 1960; Costa, 1994). При наличии сильной нелинейности расширенный фильтр Калмана приводит к плохим результатам оценки из-за распространения ковариации от одного шага измерения к другому посредством линеаризации (Bishop and Welch, 2001).Другими словами, использование якобианов, представляющих все частные производные нелинейной системы (модели), может привести к неоптимальной работе, а иногда и расходимости расширенного фильтра Калмана. Поэтому в Коста (1994) введен фильтр Калмана без запаха (UKF) для улучшения производительности оценки, а также для устранения требований к вычислениям якобианов. UKF точно решает проблему EKF, используя подход детерминированной выборки. UKF аппроксимирует распределение состояний с помощью GRV (гауссовой случайной величины), а также с помощью EKF, но оно представлено с использованием минимального набора тщательно выбранных точек выборки.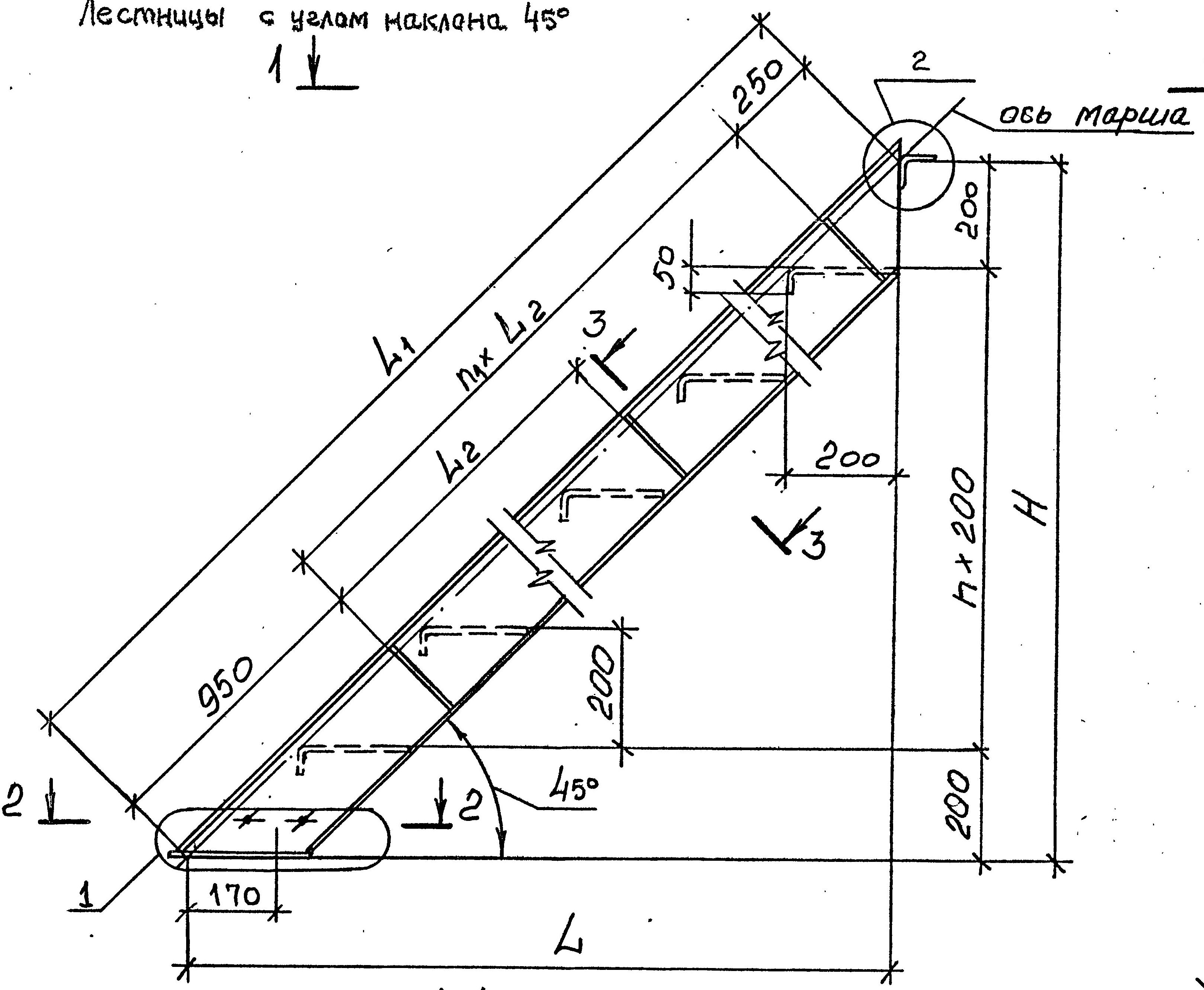
Расширенный фильтр Калмана предполагает, что состояние на временном шаге k вычисляется из предыдущего шага состояния x k −1 в соответствии с:
xk=f(xk-1,uk)+wk,zk=h(xk)+vk. (8)В общей системе либо функция перехода состояний f , либо функция измерения h , либо обе могут быть нелинейными. Здесь шумы процесса и измерения ( w k и v k ) входят в систему линейно, но могут быть системы, для которых шум нельзя считать аддитивным.к. (9)
На каждом временном шаге линеаризация выполняется локально, и результирующие матрицы Якоби J F и J H затем используются в шагах прогнозирования и коррекции алгоритма KF. Шум системы и измерения соответственно w k и v k предполагаются независимыми, белыми и с нормальным распределением вероятностей как:
p(w)~N(0,Q),p(v)~N(0,R). к-)
к-)(3) Обновить ковариацию ошибки
Pk=(I-KkJH)Pk-
Если система нелинейна и может быть хорошо аппроксимирована линеаризацией, то EKF является хорошим вариантом для оценки состояния.Однако у него есть следующие недостатки:
1. Вычисление якобианов может быть затруднено, если их необходимо вычислить численно.
2. При численном расчете якобианов требуются большие вычислительные затраты.
3. EKF работает только с системами, имеющими дифференцируемую модель.
4. EKF не является оптимальным, если система сильно нелинейна (линеаризация не дает хорошего приближения для сильно нелинейных систем).
Фильтр Калмана без запаха (UKF) можно использовать для преодоления последнего недостатка EKF путем аппроксимации распределения вероятностей вместо аппроксимации нелинейной функции.Краткое сравнение KF, EKF и UKF представлено в таблице 1 с учетом основных принципов фильтрации. Вычислительная стоимость фильтра Калмана зависит также от времени расчета измерений, которое находится в центре внимания этой статьи.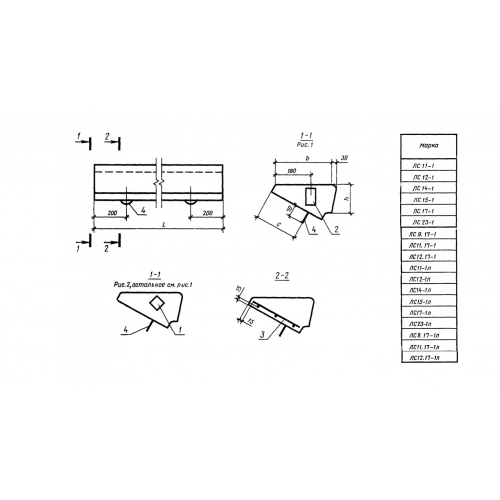
Таблица 1 . Сравнение KF, EKF и UKF по основным принципам фильтрации.
5. Расширенный/без запаха фильтр Калмана с переменным размером шага
В разделе 4 кратко объяснена процедура стандартного расширенного/неароматизированного фильтра Калмана и, соответственно, схема предиктор-корректор.В следующем разделе предлагается и подробно обсуждается фильтр Калмана с переменным размером шага (расширенный/без запаха) для повышения производительности (расширенного/без запаха) фильтра Калмана при проблемах жесткости/переключения. Предлагаемый подход состоит из концепций обработки событий и пересечения нуля в соответствии с решателями ОДУ с интеграцией переменного размера шага. Основная блок-схема фильтра Калмана с переменным размером шага графически и математически определена на рисунке 1 и в алгоритме (1).
Рисунок 1 .Процедура обработки событий с переменным размером шага Фильтр Калмана.
Алгоритм 1: Переменный размер шага Расширенный фильтр Калмана
Алгоритм начинается с инициализации предварительных условий фильтра Калмана, например, начальных состояний, ковариационных матриц и начального шага расчета (ST).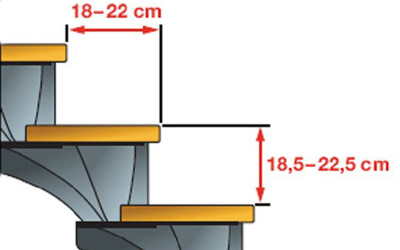 На первом этапе (уровень инициализации) или в случае возникновения и обнаружения события в процессе решения (снижение или увеличение ЗС) модель пространства состояний системы дискретизируется на основе нового ЗС.Поскольку вектор измерения является постоянным, требуется интерполяция для определения вектора измерения в соответствии с новым шагом расчета. Процедура фильтра Калмана решается от нулевого момента до текущего времени, чтобы найти подходящее начальное значение для предстоящего времени. На каждом шаге схемы предиктор-корректор используется нововведение Фильтр Калмана для процедуры обработки событий (детально показано на рисунке 1). Предлагаемый алгоритм обработки событий состоит из двух основных частей: ограничения ST и ослабления ST.В качестве расчетных параметров рассматриваются четыре параметра (мин. ST, макс. ST, α и β). Параметры α и β обозначают верхний и нижний пороги точности и определяют компромисс между временем вычислений и точностью оценки. Их в. СТ и макс. ST определены, чтобы показать максимальное и минимальное возможное время выборки, которое должно быть определено в соответствии с желаемой производительностью.
На первом этапе (уровень инициализации) или в случае возникновения и обнаружения события в процессе решения (снижение или увеличение ЗС) модель пространства состояний системы дискретизируется на основе нового ЗС.Поскольку вектор измерения является постоянным, требуется интерполяция для определения вектора измерения в соответствии с новым шагом расчета. Процедура фильтра Калмана решается от нулевого момента до текущего времени, чтобы найти подходящее начальное значение для предстоящего времени. На каждом шаге схемы предиктор-корректор используется нововведение Фильтр Калмана для процедуры обработки событий (детально показано на рисунке 1). Предлагаемый алгоритм обработки событий состоит из двух основных частей: ограничения ST и ослабления ST.В качестве расчетных параметров рассматриваются четыре параметра (мин. ST, макс. ST, α и β). Параметры α и β обозначают верхний и нижний пороги точности и определяют компромисс между временем вычислений и точностью оценки. Их в. СТ и макс. ST определены, чтобы показать максимальное и минимальное возможное время выборки, которое должно быть определено в соответствии с желаемой производительностью.
При изменении ST схема предиктор-корректор останавливается. Согласно рисунку 1 процедура фильтра Калмана с переменным размером шага продолжается путем применения новой дискретизации модели системы и новой инициализации с использованием интерполированного вектора измерений.Процедура продолжается до последнего времени моделирования, и для каждой выборки k результаты сохраняются для выпуска в конце времени моделирования.
6. Нелинейный пример: осциллятор Ван дер Поля
Для проверки предлагаемого подхода, а именно переменного размера шага EKF/UKF, рассматривается пример осциллятора Ван дер Поля. Генератор Ван дер Поля представляет собой сильно нелинейную систему/генератор с нелинейным демпфированием. Его можно рассматривать как нежесткий или жесткий пример с учетом силы демпфирования.Эта система используется в литературе в качестве примера переключения, чтобы показать преимущества обработки событий и решателей ОДУ с переменным размером шага (Khan et al. , 2011). Поэтому он используется здесь для иллюстрации преимуществ предлагаемого переменного размера шага EKF/UKF, включая процедуру обработки событий. Динамика осциллятора Ван-дер-Поля развивается во времени согласно следующему дифференциальному уравнению второго порядка:
, 2011). Поэтому он используется здесь для иллюстрации преимуществ предлагаемого переменного размера шага EKF/UKF, включая процедуру обработки событий. Динамика осциллятора Ван-дер-Поля развивается во времени согласно следующему дифференциальному уравнению второго порядка:
, где x обозначает координату положения как функцию времени, а μ — скалярный параметр, представляющий нелинейность и силу демпфирования.Уравнения становятся все более жесткими по мере увеличения μ, а при μ = 0 система становится линейной. Система (уравнение 11) может быть переписана в форме пространства состояний как:
[x1⋅(t)x2⋅(t)]=[ x2(t)µ(1-x12(t))x2(t)-x1(t)][x1(t)x2(t)], (12 )с вектором состояния [x1x2]T, описывающим первое и второе состояния системы Ван-дер-Поля. Соответственно, эйлерова дискретизация первого порядка уравнений движения осциллятора Ван-дер-Поля рассчитывается как:
с,
xk=[x1,k x2,k]T,f(xk)=[ x1,k+hx2,kx2,k+h(µ(1-x1,k2)x2,k-x1,k)], (14 ), где ч обозначает предполагаемый шаг расчета для процедуры дискретизации. k с использованием измерений с учетом различных подходов, а именно EKF, UKF, VSEKF и VSUKF, и для сравнения эффективности оценки.
k с использованием измерений с учетом различных подходов, а именно EKF, UKF, VSEKF и VSUKF, и для сравнения эффективности оценки.
7. Численные результаты и обсуждение
Для исследования производительности предлагаемого улучшенного EKF/UKF с использованием алгоритма переменного размера шага, представленного в этой статье, результаты моделирования были получены с использованием системы осциллятора Ван-дер-Поля. Системные параметры, используемые в этом исследовании моделирования, ковариации KF и параметры шума считаются идентичными для всех моделей.Результаты моделирования проиллюстрированы как оценка x 1 на рисунке 2, оценка x 2 на рисунке 3 и, соответственно, фазовый портрет на рисунке 4 для EKF и VSEKF. Производительность измеряется на основе оценочных состояний и соответствующего сравнения с реальными. Из результатов можно сделать вывод, что использование алгоритма переменного размера шага в сочетании с EKF обеспечивает лучшую производительность в задаче оценки, особенно при быстром поведении системы (жестком поведении).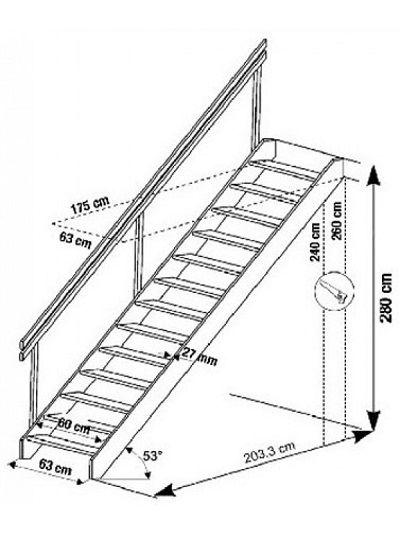 Другими словами, предлагаемое решение улучшает результаты оценивания за счет уменьшения размера шага в процедуре схемы предиктор-корректор и в случае быстрого динамического поведения (время ∈ [0,2, 0,4]). С другой стороны, уменьшая размер шага, когда не существует быстрых изменений, предлагаемый подход уменьшает большое вычислительное время схемы предиктор-корректор (время ∈ [0,6, 1,6]).
Другими словами, предлагаемое решение улучшает результаты оценивания за счет уменьшения размера шага в процедуре схемы предиктор-корректор и в случае быстрого динамического поведения (время ∈ [0,2, 0,4]). С другой стороны, уменьшая размер шага, когда не существует быстрых изменений, предлагаемый подход уменьшает большое вычислительное время схемы предиктор-корректор (время ∈ [0,6, 1,6]).
Рисунок 2 . Оценка первого состояния осциллятора Ван дер Поля x 1 с использованием расширенного фильтра Калмана с фиксированным и переменным размером шага.1) иллюстрируется для EKF, UKF, VSEKF и VSUKF. На правом рисунке результаты получены с учетом того, что время расчета известно для EKF и UKF, а на левом рисунке представлены результаты, связанные с неизвестным временем расчета. Из результатов можно заявить, что даже если время выборки известно для процедуры EKF и UKF, предлагаемые VSEKF и VSUKF обеспечивают лучшую производительность оценки, а именно почти нулевую медианную ошибку и улучшенные минимальные и максимальные значения ошибок. Результаты оценки приведены в таблице 2.Из численных результатов видно, что использование предложенного алгоритма переменного размера шага приводит к меньшему значению RMSE и MAE для VSEKF и VSUKF.
Результаты оценки приведены в таблице 2.Из численных результатов видно, что использование предложенного алгоритма переменного размера шага приводит к меньшему значению RMSE и MAE для VSEKF и VSUKF.
Рисунок 5 . Ошибка оценки состояния осциллятора Ван-дер-Поля x 1 с использованием расширенного/без запаха фильтра Калмана с фиксированным и переменным размером шага.
Таблица 2 . Сравнение производительности.
В следующей части моделирования изменяется измерение и дисперсия системного шума, и для всех фильтров рассчитывается RMSE.Результаты проиллюстрированы на рисунке 6 с логарифмической осью дисперсии шума. Из результатов можно сделать вывод, что предлагаемый подход дает более надежные результаты оценки, особенно при наличии шума измерений. RMSE увеличивается для EKF и UKF за счет увеличения дисперсии шума, в то время как это более или менее не влияет на результаты оценки VSEKF и VSUKF. В заключение можно констатировать, что предлагаемый подход превосходит современные решения по различным параметрам, которые стоит учитывать при работе с нелинейными и/или жесткими системами.
Рисунок 6 . Среднеквадратическая ошибка (RMSE) EKF/UKF и VSEKF/VSUKF с учетом различного уровня шума системы и измерений.
8. Скорость сходимости и выбор параметров VSEKF/VSUKF
Как упоминалось в разделе 5, проектные параметры α и β определяются как верхний и нижний пороги для управления инновациями ошибки оценки и вычислительными затратами соответственно. На рисунке 7 показано среднеквадратичное отклонение предлагаемого подхода для изменения проектных порогов α и β.На рисунке 7A рассматривается общее время оценки, а на рисунке 7B показана ошибка оценки в первые 3 с для оценки скорости сходимости предлагаемого подхода. Из результатов можно сделать вывод, что верхний порог α оказывает основное влияние на эффективность оценивания, и при увеличении значения α производительность снижается. Кроме того, можно сделать вывод, что приращение порога β оказывает меньшее влияние на ошибку оценивания и скорость сходимости. Худшая производительность связана со случаем, когда оба порога увеличены (как и ожидалось).
Рисунок 7 . Среднеквадратическая ошибка (RMSE) VSEKF с учетом различных параметров α и β, (A) RMSE общей ошибки оценки, (B) RMSE ошибки сходимости за первые 3 с.
Следующий анализ связан с влиянием ограничивающего/ослабляющего параметра d (который, как считается, изменяет размер шага) на производительность оценки. Согласно рисунку 8 RMSE обычно уменьшается при увеличении параметра d и увеличивается, когда d > 1.
Рисунок 8 . Среднеквадратическая ошибка (RMSE) VSEKF с учетом изменения параметров d (параметр ограничения/ослабления).
На рис. 9 показано влияние ковариаций системного шума и шума измерений на эффективность оценки. В соответствии с результатом производительность снижается при ковариации шума системы 0 < Q < 100 и ковариации шума измерений 250 < R < 800 (эта область показана красными стрелками на рис.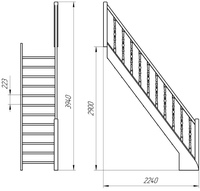 9).
9).
Рисунок 9 . Среднеквадратическая ошибка (RMSE) VSEKF с учетом вариации системы и ковариаций шума измерений.
9. Резюме, выводы и перспективы
Алгоритм фильтра Калмана с переменным размером шага (расширенный/без запаха) (VSEKF/VSUKF), предложенный в этой статье, основан на обработке событий и концепциях пересечения нуля, используемых в структуре решателей обыкновенных дифференциальных уравнений. На каждом шаге схемы предиктор-корректор используется инновация Расширенный/Бездушный фильтр Калмана для обнаружения событий с учетом предопределенных нижней и верхней границ (α и β).В случае, если событие произошло и обнаружено, время выборки увеличивается (ослабляющая процедура) или уменьшается (ограничивающая процедура), схема предиктор-корректор останавливается, и процедура продолжается путем новой дискретизации модели системы и новой инициализации с использованием интерполированный вектор измерения. В случае, если событие не обнаружено, схема предиктор-корректор может быть продолжена с текущим рассматриваемым СТ. Считается, что параметры проекта α и β контролируют и влияют на производительность и время вычислений.
Считается, что параметры проекта α и β контролируют и влияют на производительность и время вычислений.
Пример Ван дер Пола используется в качестве общего примера для жестких систем, чтобы проиллюстрировать преимущества предлагаемого подхода по сравнению со стандартным дискретным фильтром Калмана с расширенным/без запаха. Результаты моделирования наглядно демонстрируют эффективность предложенного подхода к оценке, особенно вблизи быстрых изменений в динамике системы (жесткое поведение). Другими словами, предлагаемое решение повышает производительность оценивания за счет уменьшения размера шага в процедуре схемы предиктор-корректор в соответствии с текущей точностью оценивания и в случае быстрого динамического поведения.Из результатов моделирования также можно сделать вывод, что предложенный EKF/UKF с переменным шагом более надежен при наличии высокого уровня шума системы/измерения по сравнению со стандартным EKF/UKF.
Что не охвачено и может быть обнаружено как ограничение этой работы, так это вычислительные усилия.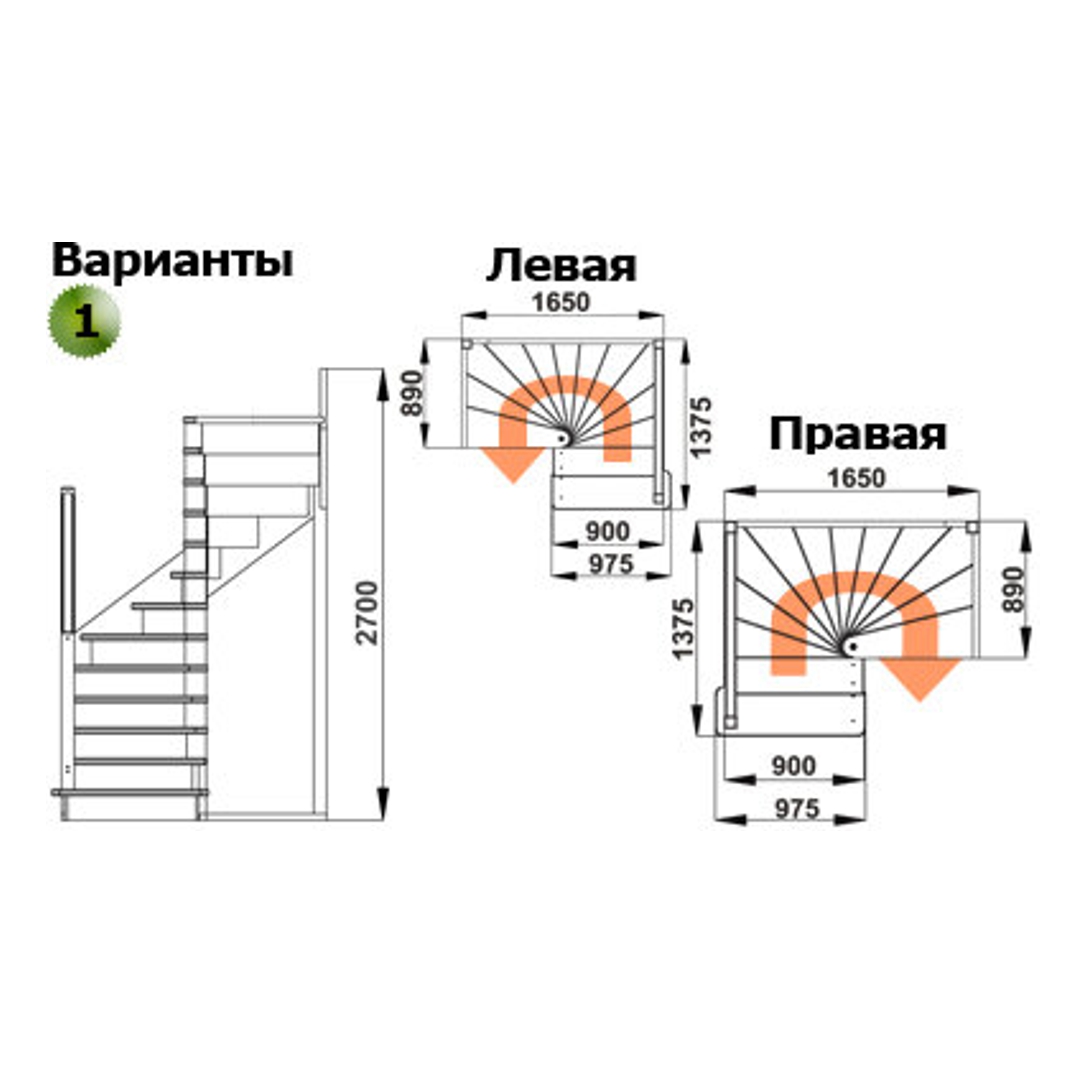 Исследование вычислительных усилий, связанных с предлагаемым управлением размером шага, и его последствия не рассматриваются в этом вкладе. Вычислительное время, необходимое для предлагаемого подхода, больше, чем для стандартного EKF/UKF, за счет уменьшения размера шага.С другой стороны, в процедуре релаксации время вычислений уменьшается. Таким образом, исследование определения параметров и пороговых значений в отношении реализации в реальном времени кажется полезным и может рассматриваться как будущая работа.
Исследование вычислительных усилий, связанных с предлагаемым управлением размером шага, и его последствия не рассматриваются в этом вкладе. Вычислительное время, необходимое для предлагаемого подхода, больше, чем для стандартного EKF/UKF, за счет уменьшения размера шага.С другой стороны, в процедуре релаксации время вычислений уменьшается. Таким образом, исследование определения параметров и пороговых значений в отношении реализации в реальном времени кажется полезным и может рассматриваться как будущая работа.
Заявление о доступности данных
Необработанные данные, подтверждающие выводы этой статьи, будут предоставлены авторами без неоправданных оговорок любому квалифицированному исследователю.
Вклад авторов
FB и DS задумали представленную идею, разработали теорию, выполнили расчеты и проверили аналитические методы.Все авторы обсудили результаты и внесли свой вклад в окончательный вариант рукописи.
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.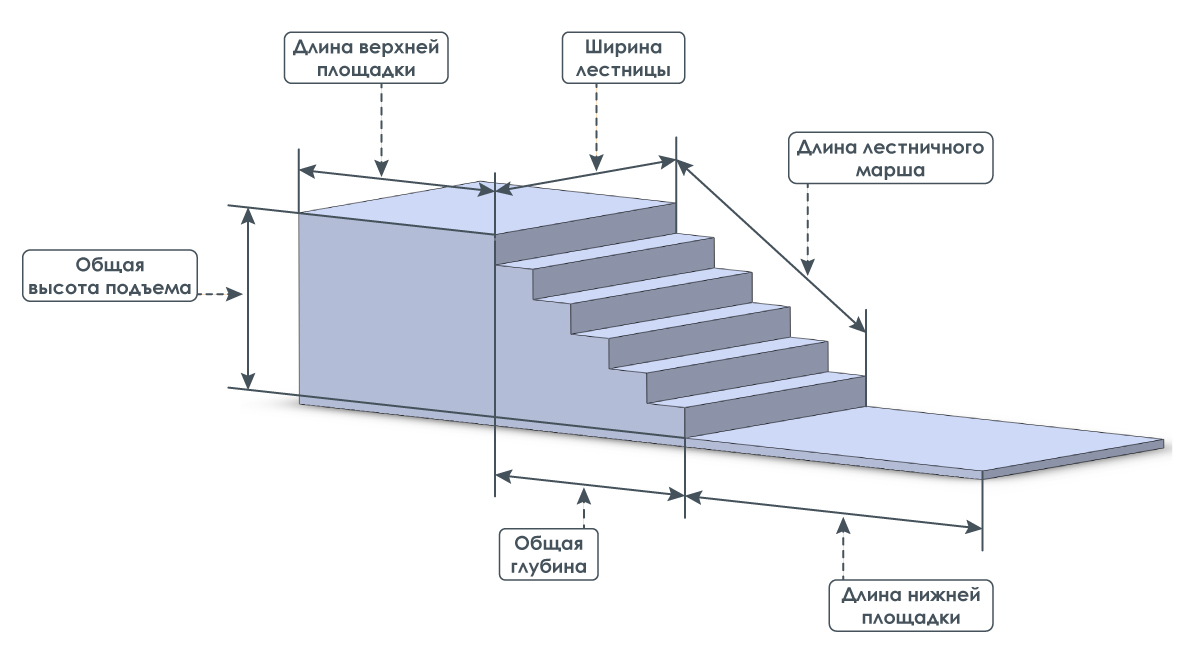
Благодарности
Благодарим за поддержку Фонд публикаций открытого доступа Университета Дуйсбург-Эссен.
Ссылки
Андерсон Б. и Мур Дж.(2012). «Оптимальная фильтрация», в Dover Books on Electrical Engineering , ed T. Kailath (Dover Publications; Университет Ньюкасла).
Академия Google
Ашино, Р., Нагасе, М., и Валланкур, Р. (2000). За и за пределами комплекта Matlab ode. Вычисл. Мат. заявл. 40, 491–512. doi: 10.1016/S0898-1221(00)00175-9
Полнотекстовая перекрестная ссылка | Академия Google
Аткинсон, К., Хан, В., и Стюарт, Д. (2011). Численное решение обыкновенных дифференциальных уравнений .Нью-Йорк, штат Нью-Йорк: John Wiley & Sons.
Академия Google
Бахшанде, Ф., и Сёффкер, Д. (2015). «Реконструкция нелинейных характеристик с помощью передовых подходов к проектированию наблюдателей», в ASME 2015 Dynamic Systems and Control Conference , 2:V002T23A007. дои: 10. 1115/DSCC2015-9897
1115/DSCC2015-9897
Полнотекстовая перекрестная ссылка | Академия Google
Бахшанде, Ф., и Сёффкер, Д. (2018). «Фильтр Калмана с переменным размером шага с использованием алгоритма обработки событий для систем переключения», в ASME 2018 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (Quebec, QC) 6:V006T09A013.
Академия Google
Белл, Б.М., и Кэти, Ф.В. (1993). Итерированное обновление фильтра Калмана как метод Гаусса-Ньютона. IEEE Trans. автомат. Контроль 38, 294–297.
Академия Google
Бернал, Д. (1991). Локализация событий при пошаговом интегрировании уравнений движения. Дж. Структура. англ. 117, 530–545.
Академия Google
Чатци, М. Н., и Чатци, Е. Н. (2017). Прерывистый фильтр Калмана без запаха для негладких динамических задач. Перед. Построенная среда. 3:56. doi: 10.3389/fbuil.2017.00056
Полнотекстовая перекрестная ссылка | Академия Google
Коста, П. Дж. (1994). Архитектура адаптивной модели и расширенные фильтры Калмана-Бьюси. IEEE Trans. Аэрокосмическая электр. Сист. 30, 525–533. дои: 10.1109/7.272275
Дж. (1994). Архитектура адаптивной модели и расширенные фильтры Калмана-Бьюси. IEEE Trans. Аэрокосмическая электр. Сист. 30, 525–533. дои: 10.1109/7.272275
Полнотекстовая перекрестная ссылка | Академия Google
Эспозито, Дж. М., и Кумар, В. (2007). Алгоритм обнаружения событий состояния для численного моделирования гибридных систем с особенностями модели. ACM Trans. Модель. вычисл. Модел. 17:1. дои: 10.1145/1189756.1189757
Полнотекстовая перекрестная ссылка | Академия Google
Хайрер, Э., и Ваннер, Г. (1987). Решение обыкновенных дифференциальных уравнений II . Нью-Йорк, штат Нью-Йорк: Спрингер.
Академия Google
Гавлик, Дж., и Страка, О. (2015). Оценка производительности повторного расширенного фильтра Калмана с переменной длиной шага. J. Phys. Серия конференций 659:12022. дои: 10.1088/1742-6596/659/1/012022
Полнотекстовая перекрестная ссылка | Академия Google
Кальман, Р. Э. (1960). Новый подход к задачам линейной фильтрации и прогнозирования. J. Fluids Eng. 82, 35–45.
Э. (1960). Новый подход к задачам линейной фильтрации и прогнозирования. J. Fluids Eng. 82, 35–45.
Академия Google
Хан, Дж. А., Куреши, И. М., и Раджа, М. А. З. (2011). Гибридный эволюционный вычислительный подход: приложение к осциллятору Ван дер Поля. Междунар. Дж. Физ. науч. 6, 7247–7261. doi: 10.5897/IJPS11.922
Полнотекстовая перекрестная ссылка | Академия Google
Ню, Ю., Конг, Ю., и Ву, Л. (2018). Инициированный событием непрерывный дискретный фильтр Калмана с контролируемой ошибкой оценки. Доступ IEEE 6, 42482–42496. doi: 10.1109/ACCESS.2018.2860626
Полнотекстовая перекрестная ссылка | Академия Google
Скоглунд, М. А., Хендеби, Г., и Эксхилл, Д. (2015). «Расширенные модификации фильтра Калмана на основе точки зрения оптимизации», в , 2015 г., 18-я Международная конференция по объединению информации, (Вашингтон, округ Колумбия), 1856–1861.
Академия Google
Сёффкер, Д. , Ю, Т.Дж., и Мюллер, П.С. (1995). Оценка состояния динамических систем с нелинейностями с помощью пропорционально-интегрального наблюдателя. Междунар. Дж. Сист. науч. 26, 1571–1582.
, Ю, Т.Дж., и Мюллер, П.С. (1995). Оценка состояния динамических систем с нелинейностями с помощью пропорционально-интегрального наблюдателя. Междунар. Дж. Сист. науч. 26, 1571–1582.
Академия Google
Соренсон, HW (1960). Фильтрация Калмана: теория и применение . Нью-Йорк, штат Нью-Йорк: IEEE Press.
Академия Google
Сули, Э. (2001). Численное решение обыкновенных дифференциальных уравнений . Математический институт Оксфордского университета, конспект лекций.
Академия Google
Ван, М., и Ли, П.Ю. (2008). «Наблюдатель фильтра Калмана на основе событий для поворотного высокоскоростного двухпозиционного клапана», , 2008 г., Американская конференция по управлению, (Сиэтл, Вашингтон: IEEE), 1546–1551.doi: 10.1109/ACC.2008.4586711
Полнотекстовая перекрестная ссылка | Академия Google
Ван Ю., Карими Х. Р., Лам Х.-К. и Ян Х. (2019). Нечеткое управление отслеживанием выходных данных и фильтрация для нелинейных дескрипторных систем с дискретным временем при ненадежных каналах связи. IEEE Trans. Кибернет . 1–11. doi: 10.1109/TCYB.2019.2920709
IEEE Trans. Кибернет . 1–11. doi: 10.1109/TCYB.2019.2920709
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Ван Ю., Ся Ю., Шен Х. и Чжоу П. (2017). Smc-дизайн для робастной стабилизации нелинейных сингулярных систем с марковскими скачками. IEEE Trans. Автомат. Контроль 63, 219–224. doi: 10.1109/TAC.2017.2720970
Полнотекстовая перекрестная ссылка | Академия Google
Вт, Х. (1984). Управление размером шага в Ode Solvers . Технический отчет, Sandia National Labs, Альбукерке, Нью-Мексико, США.
Академия Google
Райт, Дж. П., и Пей, Дж.-С. (2012). Решение динамических систем с кусочно-возвращающей силой с использованием положения события состояния. Дж. Инж. мех. 138, 997–1020.doi: 10.1061/(ASCE)EM.1943-7889.0000404
Полнотекстовая перекрестная ссылка | Академия Google
Чжан Ф., Йедданапуди М. и Мостерман П. Дж. (2008). Алгоритмы определения местоположения и обнаружения пересечения нуля для моделирования гибридных систем.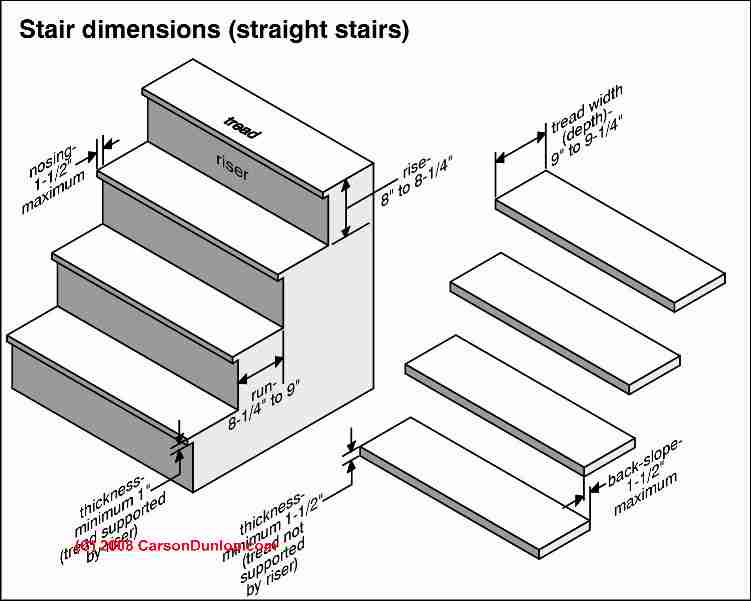 МФБ Проц. Том. 41, 7967–7972. doi: 10.3182/20080706-5-KR-1001.01346
МФБ Проц. Том. 41, 7967–7972. doi: 10.3182/20080706-5-KR-1001.01346
Полнотекстовая перекрестная ссылка | Академия Google
Двухточечные методы градиента размера шага | Журнал численного анализа IMA
Получить помощь с доступом
Институциональный доступ
Доступ к контенту с ограниченным доступом в Oxford Academic часто предоставляется посредством институциональных подписок и покупок.Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту следующими способами:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с проверкой подлинности IP.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения.
Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Щелкните Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением.Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Вход с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Многие общества предлагают своим членам доступ к своим журналам с помощью единого входа между веб-сайтом общества и Oxford Academic. Из журнала Oxford Academic:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Некоторые общества используют личные аккаунты Oxford Academic для своих членов.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.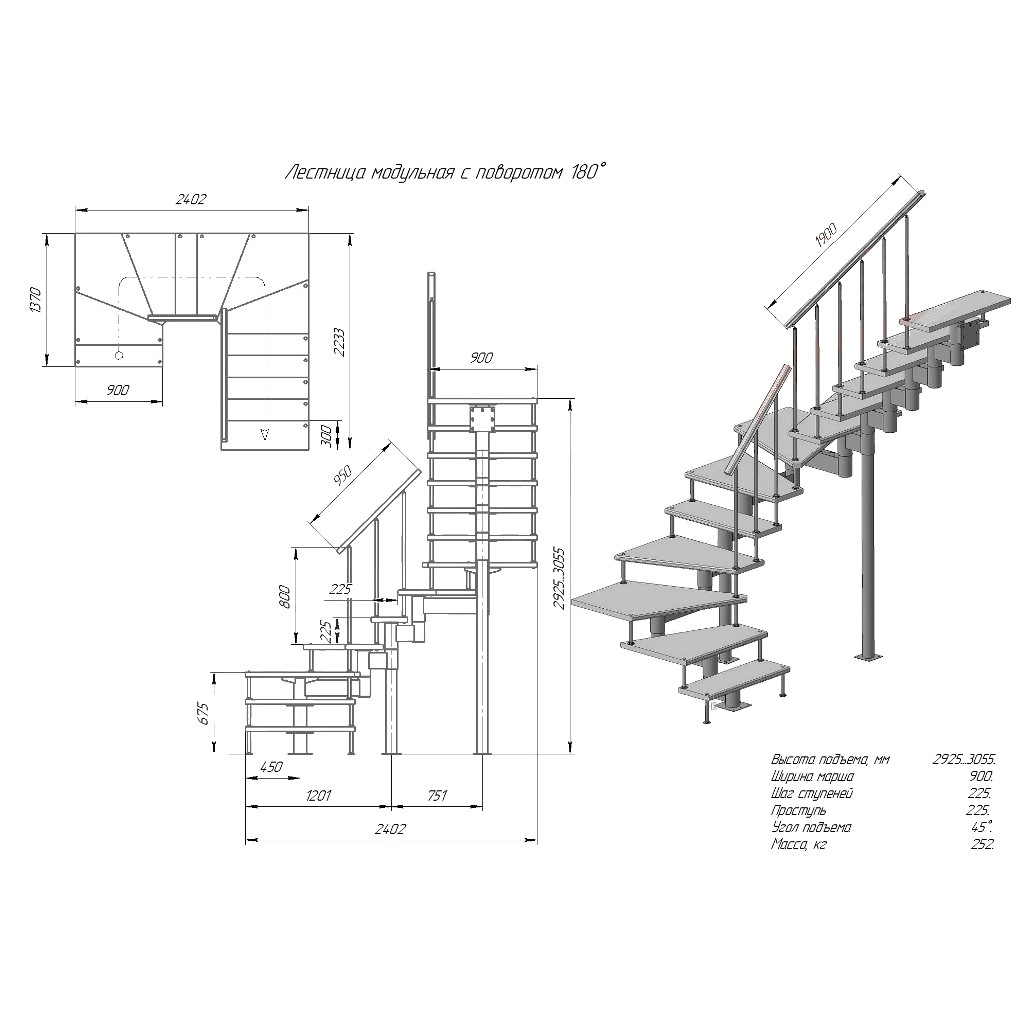
Некоторые общества используют личные учетные записи Oxford Academic для предоставления доступа своим членам.
Институциональная администрация
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
Просмотр ваших зарегистрированных учетных записей
Вы можете одновременно войти в свою личную учетную запись и учетную запись своего учреждения.Щелкните значок учетной записи в левом верхнем углу, чтобы просмотреть учетные записи, в которые вы вошли, и получить доступ к функциям управления учетной записью.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ.
Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ.
Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
— SIMION 2020 Supplemental Documentation
Когда SIMION вычисляет траекторию частицы, он разбивает кривую траектории на много маленьких шагов.Каждый шаг траектории вычисляется последовательно. Продолжительность времени, которое частица тратит на каждый шаг, называется временным шагом . Шаги времени (как и все времена в SIMION) имеют единицы микросекунд, и они могут меняться неравномерно по траектории.
Важность размера временного шага
Размер временного шага оказывает значительное влияние на точность и производительность. Меньшие шаги обычно повышают точность, но требуют больше времени для вычислений, потому что там больше шагов.
Размер временного шага легко изменить, часто гораздо быстрее и проще, чем
другие факторы, влияющие на точность (например,г. размер блока сети PA).
размер блока сети PA).
Визуализация временных шагов
Временные шаги могут быть визуализированы. При использовании Fly’m на траектории каждого события записи данных будет отображаться красная точка. Итак, включите запись данных с включенным событием «Каждый шаг Иона». Вы также можете записать значения времени полета (TOF) или положения (X/Y/Z), для более количественного отображения размеров временных шагов в окне/файле журнала:
Затем на экране просмотра отображаются красные точки, а время печатается в журнале:
В приведенном выше примере с Einzel шаги по времени обычно
соответствующее перемещению примерно на одну единицу сетки потенциальной решетки (1 gu).В некоторых более критических областях, требующих более высокой точности
(вход/выход из ЗУ, приближение к электродам,
изменение скорости или большая кривизна поля), размер временного шага уменьшается.
Размеры шага по времени даже увеличены в некоторых некритических областях,
как за пределами потенциальных массивов, где нет полей.
Факторы, влияющие на размер временного шага
Существует ряд факторов, влияющих на размер временного шага, каждый из которых подробно описано далее в этом документе:
- Коэффициент качества траектории (Т.Qual) на вкладке Particles, что является основным средством контроля качества траектории.
- Маркеры времени (если включены) в правой части вкладки «Частицы». может дополнительно уменьшить временные шаги до заданного количества микросекунд.
- Сегмент tstep_adjust (если имеется) в пользовательской программе рабочей среды отменяет вышеуказанные значения по умолчанию для еще более точного управления.
Коэффициент качества траектории (T.Qual)
Один из самых простых способов изменить размер временного шага — использовать коэффициент качества траектории. (Т.Качество) на экране просмотра:
Диапазон значений T.Qual от -500 до +500.
Значение по умолчанию +3 обычно разумно.
Значения T.Qual имеют следующее общее значение:
- 0 является наименее точным и определяет временные шаги таким образом, что частица проходит примерно одну единицу сетки PA за временной шаг. Более высокие значения магнитуды (как в положительном, так и в отрицательном направлении) вызывают меньшие временные шаги, что означает более длительное время выполнения, но более высокую точность.
- Отрицательные или нулевые значения вызывают шаг по времени 1/(1 + абс(tqual)) единиц сетки.
- Положительные значения (1..99) , заставляют временные шаги по умолчанию равняться 1 единице сетки.
Но это также динамически уменьшает размеры временного шага, когда
применимо для повышения точности, например, рядом с особыми областями, такими как большая кривизна поля,
изменения скорости или поверхности электродов.
Ограничение CV (влияющее на то, насколько агрессивно сокращаются временные шаги в пределах высоких
области кривизны поля) устанавливается равным 1/tqual.

- Положительные значения (100..500) , по умолчанию шаг времени 1/(1 + abs(tqual — 100)) единиц сетки, но в остальном это то же самое, что и предыдущее случае в отношении динамического уменьшения размера шага по времени с CV = 1/tqual.
Формулы T.Qual подробно описаны в Приложение «Вычислительные методы» к руководству пользователя SIMION (например, «H.23 Как контролируется качество траектории» в 8.0/8.1).
Вот несколько примеров значения T.Qual:
- Значение 0 указывает расстояние шага в 1 единицу сетки (gu).
- Значение -9 указывает расстояние шага 1/(1 + абс.(-9)) = 0,1 гу.
- Значение +9 указывает расстояние шага 1 gu и динамическое уменьшение размера шага с CV = 1/9.
- Значение 109 указывает расстояние шага 1/(1 + abs(109-100)) = 0,1 gu и динамическое уменьшение размера шага с CV = 1/9.
Наличие частиц, перемещающихся примерно на 1 единицу сетки за временной шаг
(например, T.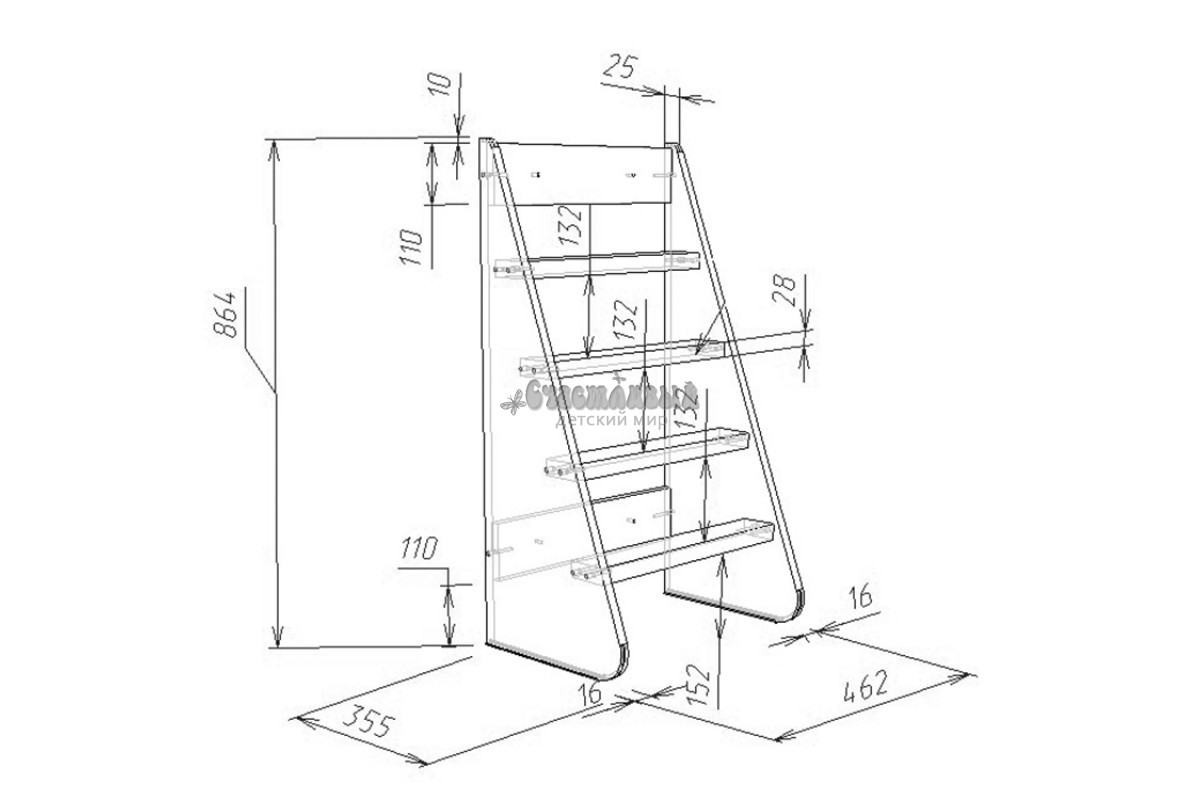 Qual 0 или 3) обычно является приемлемым. Нет необходимости делать сверхточные расчеты траектории, если вы
поля вычисляются не так точно, и нет необходимости делать супер
точные расчеты поля, если траектории ваших частиц не
рассчитал это точно.Если частицы должны были пересекать более одной единицы сетки за один временной шаг, то почему вы
тратить время на уточнение такого большого массива?
Если бы частицы пересекали небольшую часть единицы сетки за шаг времени,
тогда несовершенная интерполяция полей в пределах единицы сетки может не дать многого.
улучшение, так как точность поля соответствует единице сетки PA.
Как правило, размер единицы сетки PA (мм/gu) более важен для точности, чем T.Qual,
пока T.Qual составляет +3 или выше.
Qual 0 или 3) обычно является приемлемым. Нет необходимости делать сверхточные расчеты траектории, если вы
поля вычисляются не так точно, и нет необходимости делать супер
точные расчеты поля, если траектории ваших частиц не
рассчитал это точно.Если частицы должны были пересекать более одной единицы сетки за один временной шаг, то почему вы
тратить время на уточнение такого большого массива?
Если бы частицы пересекали небольшую часть единицы сетки за шаг времени,
тогда несовершенная интерполяция полей в пределах единицы сетки может не дать многого.
улучшение, так как точность поля соответствует единице сетки PA.
Как правило, размер единицы сетки PA (мм/gu) более важен для точности, чем T.Qual,
пока T.Qual составляет +3 или выше.
Иногда большие отрицательные значения (например,г. -50) или большое положительное значение (например, +50)
Значения T.Qual гарантированы, если ваши поля более точны
чем размер единицы сетки предполагает, например. однородное поле между интегрально
выровненные электроды или аналитически заданное поле с помощью efield_adjust сегмент пользовательской программы
(Улучшение поверхности электрода / единицы дробной сетки также могут повысить точность поля).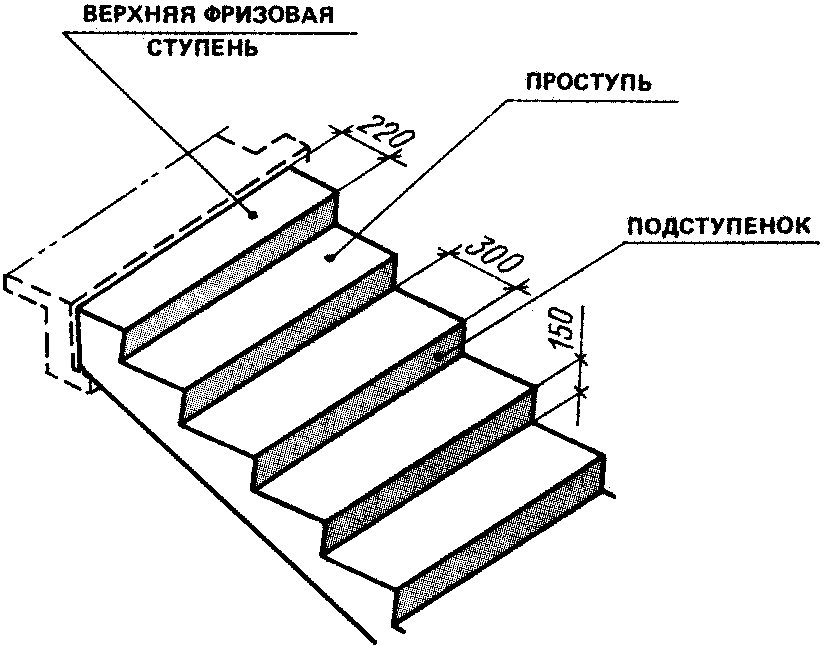
0 или отрицательные значения распространены, особенно в групповых полетах. Для группового полета (когда все частицы летят одновременно с одинаковые временные шаги), это может гарантировать 0 (или отрицательные значения), чтобы избежать проблема одной частицы, получающей крошечные временные шаги в специальной области и замедление расчета остальной части пака, особенно если точность не критична.Некоторые вещи, такие как столкновение ион-газ (Ion-Gas Collisions) уже внести изрядную долю неопределенности, так что точные траектории не столь критичны, и к тому же быстрое рассеивание частиц делает эффекты положительного T.Qual часто неуместны или контрпродуктивны.
Маркеры времени
Если вы включите маркеры времени (на вкладке Частицы),
временные шаги будут уменьшены, чтобы совпадать с каждым кратным
указанного времени в микросекундах.
Это может быть быстрый способ заставить временные шаги быть меньше определенного размера.
в единицах микросекунд (а не только в единицах сетки).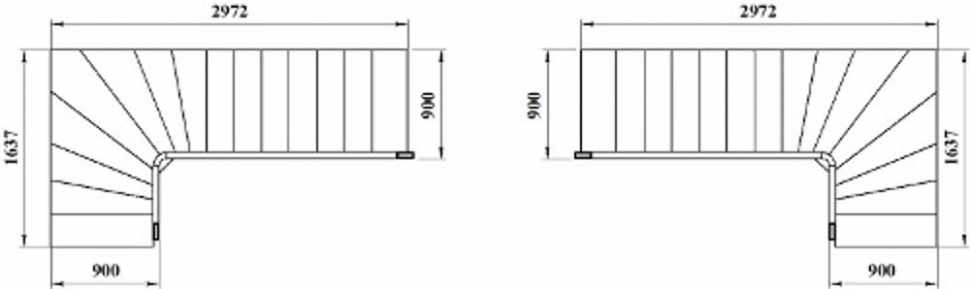 Также может быть полезно обеспечить запись данных через точные временные интервалы.
(например, как некоторые понадобились для вычисления работы FFT/ICR, быстрого преобразования Фурье (FFT)).
Также может быть полезно обеспечить запись данных через точные временные интервалы.
(например, как некоторые понадобились для вычисления работы FFT/ICR, быстрого преобразования Фурье (FFT)).
Точность и размер временного шага
Размер временного шага важен для точности, но также очень легко изменить, особенно по сравнению с размером блока сетки PA. Меньшие шаги по времени не мешают, но увеличивают время расчета траектории, хотя обычно время расчета траектории очень быстрое, поэтому мало вреда экспериментировать с меньшими временными шагами.Если вы уменьшите размеры шага по времени и не заметите разницы в траектории, значимые для вас, то это говорит о том, что размер временного шага не является основным источником ошибок для вашего моделирования, и существует мало ли нужно это делать. Вам может понадобиться только запустить одну или пару частиц, чтобы сделать это определение.
Однако необходимо убедиться, что размеры временного шага меньше любых специальное поведение, которое вы хотели бы смоделировать в меньшем масштабе времени:
- Радиочастотные поля (см.
 Поле, зависящее от времени) должны иметь меньшие временные шаги
чем некоторая доля периода РЧ, чтобы частицы могли видеть
форму волны RF точно или вообще.(См. Пример SIMION: октуполь.)
Поле, зависящее от времени) должны иметь меньшие временные шаги
чем некоторая доля периода РЧ, чтобы частицы могли видеть
форму волны RF точно или вообще.(См. Пример SIMION: октуполь.) - Зависящие от времени поля (Time-Dependent Field) с резкими переходами напряжения может потребовать более тонкого контроля, так что временной шаг заканчивается именно на переходах напряжения. (См. Пример SIMION: группировщик, Пример SIMION: форма сигнала и «examplesfaims*wavelib.lua».)
- Временные шаги вблизи границ (кроме встроенной SIMION обработки границ электродов), например, для программируемого Test Plane может потребоваться временные шаги, чтобы закончить на этой границе, если требуется максимальная точность.(См. Пример SIMION: test_plane.)
- Модели столкновений , особенно те, которые моделируют каждое ионно-нейтральное взаимодействие,
как модель твердой сферы (модель столкновения HS1),
может потребовать, чтобы размер временного шага был меньше некоторого
долю среднего свободного времени между столкновениями для точного моделирования
столкновения.
 (См. Пример SIMION: Collision_hs1.)
(См. Пример SIMION: Collision_hs1.) - Поля, которые оказались гораздо более точными , чем можно предположить по размеру ячейки сетки PA (например, однородные поля между электродами, выровненными по сетке, или поля, определенные аналитически с сегментом efield_adjust), может существенно выиграть от меньшего времени шаги.
Более правильный способ уменьшить эти временные шаги для точного управления
часто является сегментом tstep_adjust ,
хотя увеличивая фактор T.Qual или даже используя маркеры времени,
может быть простым и грязным решением, избегая любых
программирование, предполагая, что время расчета траектории частицы не является проблемой
в вашей симуляции.
См. Точность для многих других вещей, влияющих на точность.
tstep_adjust Сегмент в программе пользователя
Если вам нужен больший контроль над временными шагами, вы можете определить ion_time_step явно в сегменте tstep_adjust пользовательская программа.
Размер временного шага по умолчанию может быть переопределен в программе пользователя:
- SIMION использует различные коэффициенты (включая T.Qual, как описано выше)
определить рекомендуемую длину этого временного шага.
Это зарезервированная переменная
ion_time_step. - Если у вас определен сегмент
tstep_adjust, SIMION вызовет его сегмент со значениемion_time_step, изначально установленным на значение определено на предыдущем шаге, но этот сегмент может перезаписать значение изion_time_step. - Однако, если качество траектории (T.Qual на вкладке Particles)
положительный (не нулевой или отрицательный), то он может быть уменьшен другими факторами,
например, при приближении к поверхности электродов.
Сегмент
other_actionsувидит окончательное значениеion_time_step.
Если вы не хотите возиться с определением tstep_adjust ,
просто сделайте свой T. Qual значительно более высоким, чтобы добиться аналогичного эффекта.
Qual значительно более высоким, чтобы добиться аналогичного эффекта.
Некоторые примеры, которые изменяют размеры временного шага с помощью сегментов tstep_adjust, включают
Например (аналогично примеру октуполя):
Симион.рабочая_программа() регулируемый min_step = 0,1 -- микросекунды функция segment.tstep_adjust() -- Сохранить размер временного шага <= min_step usec. ion_time_step = min(ion_time_step, min_step) конец
Регулировка размера шага
Регулировка размера шагаРегулировка размера шага
Еще один способ использования информации об ошибке — оценка ошибки и использование этой оценки выбрать размер шага так, чтобы была достигнута желаемая точность. Например, в методе Эйлера локальная ошибка усечения
Тем не менее, вторая производная может быть вычислена с помощью разностных формул как
Таким образом, отслеживая разницу между правой частью от одного временного шага к другому
можно получить оценку ошибки усечения. Эту ошибку можно уменьшить, уменьшив t. Если
пользователь указывает критерий наибольшей оценки локальной ошибки, затем t уменьшается, чтобы соответствовать этому критерию.
Кроме того, t увеличивается до максимально возможного значения, поскольку это сокращает время вычислений. Если
локальная ошибка усечения была достигнута (и оценена) с использованием размера шага
t 1
Эту ошибку можно уменьшить, уменьшив t. Если
пользователь указывает критерий наибольшей оценки локальной ошибки, затем t уменьшается, чтобы соответствовать этому критерию.
Кроме того, t увеличивается до максимально возможного значения, поскольку это сокращает время вычислений. Если
локальная ошибка усечения была достигнута (и оценена) с использованием размера шага
t 1
и желаемая ошибка e, которая должна быть достигнута с использованием размера шага t 2
то следующий размер шага t 2 берется из
В общем, не нужно менять вещи слишком часто или слишком радикально.Таким образом, можно выбрать
не увеличивать t более чем в два раза (например, в 2) или увеличивать t более одного раза каждые столько-то
шагов (например, 5) [Rice, 1983]. В самых сложных кодах существует альтернатива изменению порядка
также метода. В этом случае ошибка усечения порядков на один больше и на один меньше
текущий оценивается, и выбор делается в зависимости от ожидаемого размера шага и работы.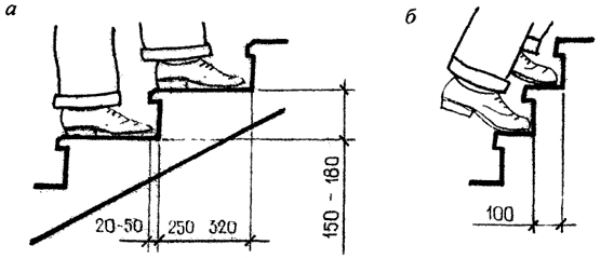
Подводя итог, можно сказать, что у нас есть два способа оценки погрешности численного решения. в зависимости от используемого нами метода.Первый вариант является наиболее распространенным, и именно его мы используем. с МАТЛАБ. В этом случае мы используем метод с переменным размером шага t, который выбирается метод, чтобы дать предполагаемую ошибку меньше, чем допуск, который мы указываем. С этим методом мы не можем использовать метод экстраполяции, поскольку t постоянно меняется, и мы не можем его контролировать; мы только контролировать толерантность. Таким образом, для оценки точности решения необходимо решить задачу при не менее двух раз с разными допусками.Если решение не меняется (по нашим меркам), то проблема является
решен достаточно точно. Мы также могли бы использовать два разных метода разного порядка. За
например, ode45 и ode23 оба являются кодами Рунге-Кутты, одного пятого порядка и одного третьего порядка.
Таким образом, сравнение результатов обоих также даст некоторое представление о точности. Таким образом, с MATLAB, необходимо решить задачу не менее двух раз, чтобы проверить
точность .Это не означает, что мы должны решать каждый случай дважды, так как мы можем вносить небольшие изменения в некоторые из них.
параметры и повторные расчеты. Однако мы должны сделать этот тест хотя бы один раз.
за проблему.
Таким образом, с MATLAB, необходимо решить задачу не менее двух раз, чтобы проверить
точность .Это не означает, что мы должны решать каждый случай дважды, так как мы можем вносить небольшие изменения в некоторые из них.
параметры и повторные расчеты. Однако мы должны сделать этот тест хотя бы один раз.
за проблему.
Во втором варианте мы сами пишем код для использования фиксированного указанного t. Мы можем сделать это в MATLAB или, например, в EXCEL. Затем применяем метод три раза и проверяем что решение находится в пределах области, в которой следуют условия ошибки.Затем мы экстраполируем на ноль t, чтобы получить точный ответ. фигура 2 показывает, что используемый метод равен O(t), и затем экстраполяция выполняется по формуле первого порядка,
Обратите внимание, что мы должны изобразить численное решение в зависимости от t в некоторой степени, так как у нас нет
точное решение для сравнения. Если мы напишем собственный код для решения дифференциальных уравнений, этот тест необходим для проверки ответа .
Возьмите домой Сообщение: Решатели ODE обычно корректируют временной шаг, чтобы попытаться достичь заданной пользователем точности.Однако для проверки точности необходимо найти по крайней мере два решения.
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{добавить в коллекцию.описание.длина}}/500 {{l10n_strings.TAGS}} {{$элемент}} {{l10n_strings.ПРОДУКТЫ}} {{l10n_strings. DRAG_TEXT}}
DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.АВТОР}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select. selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}} Размер шага
selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}} Размер шага· GitHub Размер шага
· GitHubStepsize — это SaaS-решение для измерения и управления техническим долгом
- Лондон
- https://шагразмер.ком
- проверено
Мы убедились, что организация Stepsize контролирует домен:
Закреплено
Atom git винит желоб с запросами на вытягивание, связанными проблемами и цветовым кодированием возраста кода.

Машинопись 16 3
Репозитории
- Машинопись 1 21 0 14 Обновлено 13 января 2022 г.
- атом-лучше-git-винить
Общественный
Atom git винит желоб с запросами на вытягивание, связанными проблемами и цветовым кодированием возраста кода.
Машинопись 16 Массачусетский технологический институт 3 11 14 Обновлено 20 октября 2021 г.
- 0 0 0 0 Обновлено 18 августа 2021 г.
- Машинопись 3 0 0 10 Обновлено 10 августа 2021 г.
- Оболочка 0 0 0 0 Обновлено 6 апреля 2021 г.
- github-интеграция-демонстрация
Общественный
Общедоступный репозиторий для демонстрации функциональности интеграции Stepsize <> GitHub.
Машинопись 0 1 0 1 Обновлено 21 июля 2020 г.
- Машинопись 0 Массачусетский технологический институт 36 0 0 Обновлено 14 августа 2019 г.
- шики
Общественный
Красивая подсветка синтаксиса.
Машинопись 0 119 0 0 Обновлено 8 августа 2019 г. - JavaScript
0
0
1
0
Обновлено 21 мая 2019 г.

- JavaScript 1 3 0 0 Обновлено 10 января 2019 г.
Люди
Эта организация не имеет общественных членов.Вы должны быть участником, чтобы видеть, кто является частью этой организации.
Наиболее часто используемые темы
Загрузка…
Вы не можете выполнить это действие в данный момент. Вы вошли в другую вкладку или окно. Перезагрузите, чтобы обновить сеанс. Вы вышли на другой вкладке или в другом окне. Перезагрузите, чтобы обновить сеанс.Произошла ошибка при настройке пользовательского файла cookie
Произошла ошибка при настройке пользовательского файла cookie Этот сайт использует файлы cookie для повышения производительности.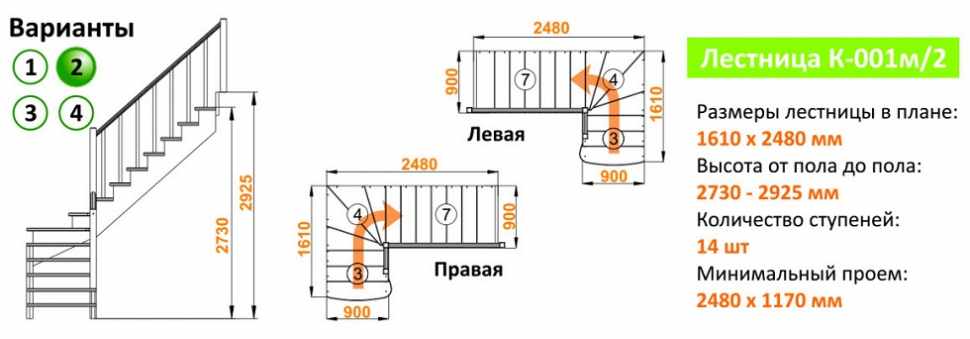 Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера на прием файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
- Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.

- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.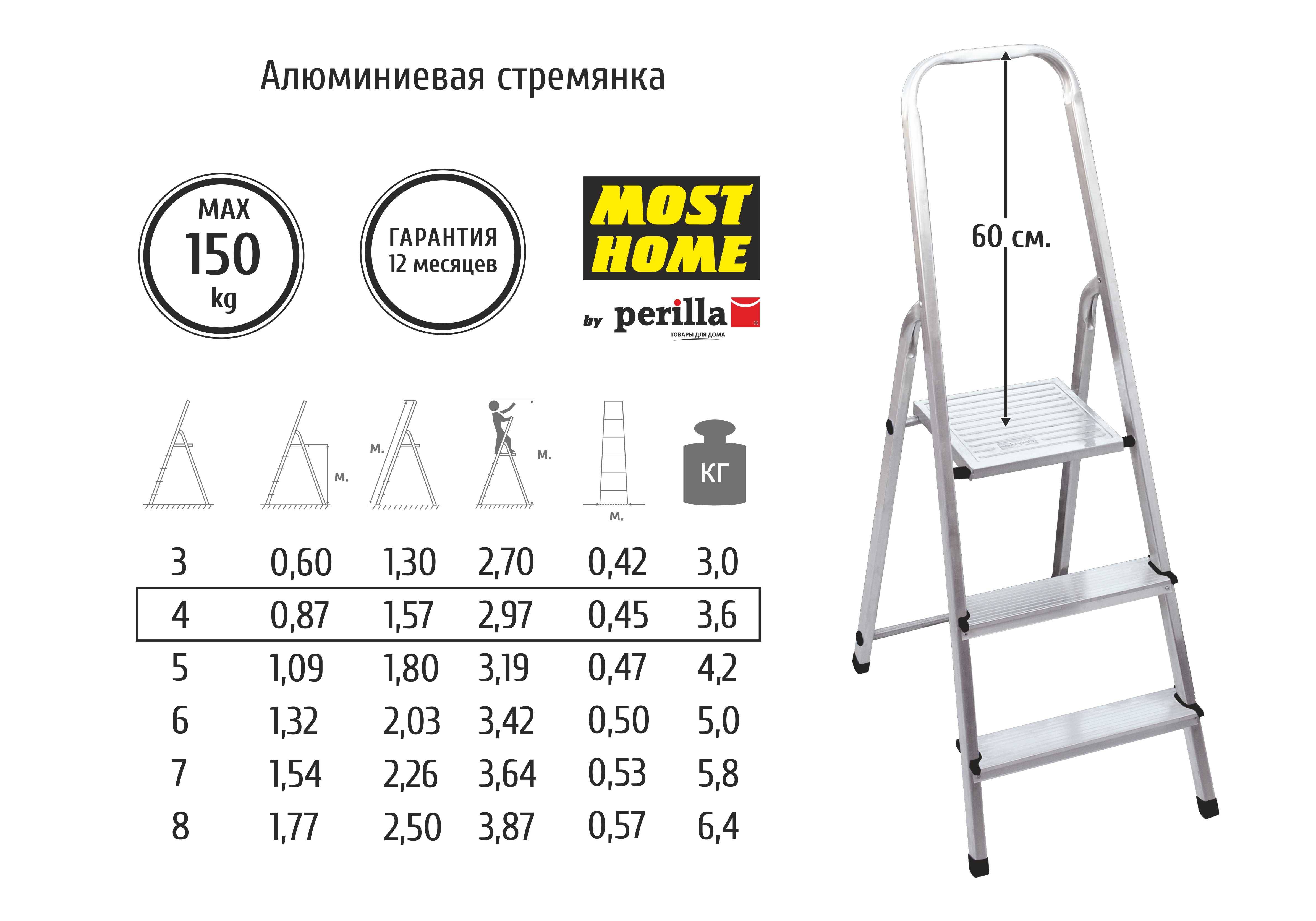

 Это необходимо для того, чтобы человек мог опереться на конструкцию всей подошвой, и она не свисала с края.
Это необходимо для того, чтобы человек мог опереться на конструкцию всей подошвой, и она не свисала с края.


 Ее размер будет равен произведению полученного остатка на исходную высоту.
Ее размер будет равен произведению полученного остатка на исходную высоту.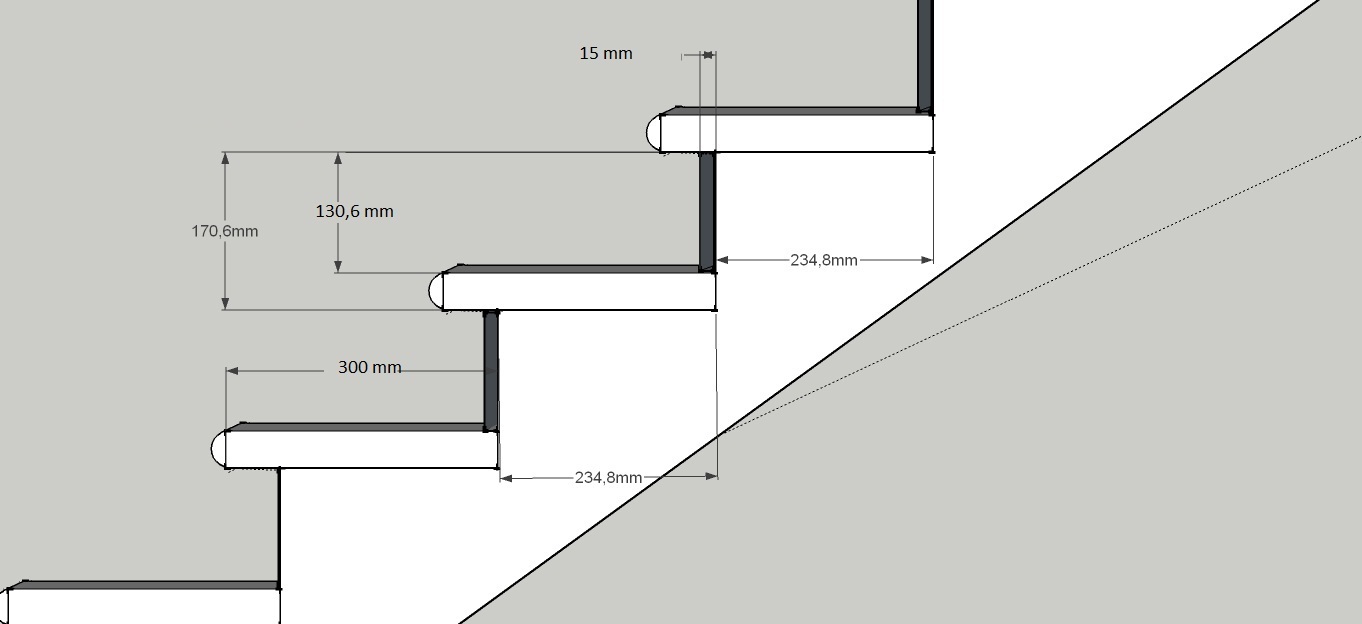


 — 316 c.
— 316 c.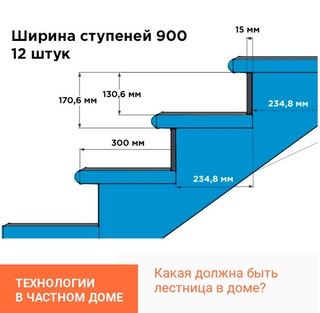
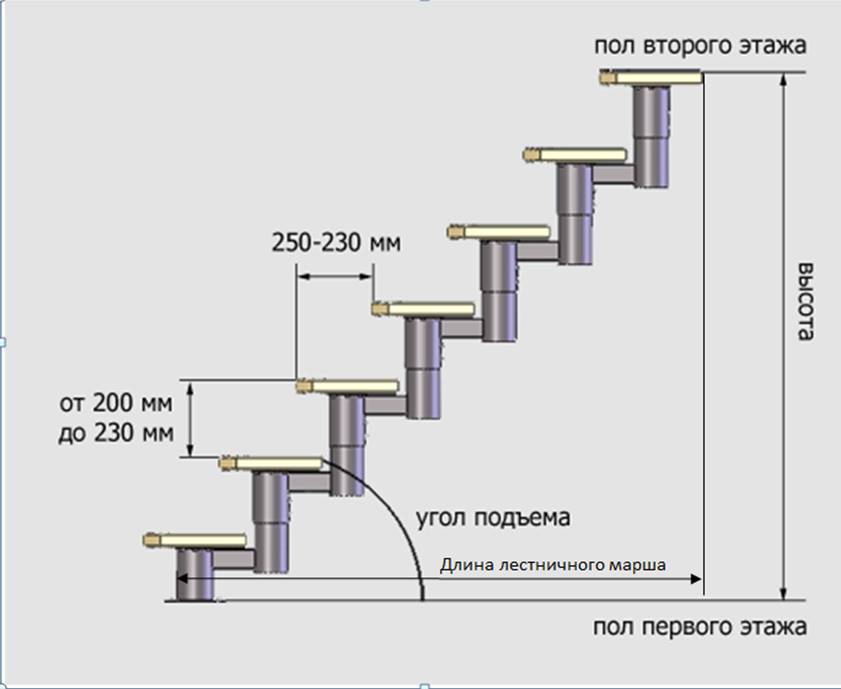 Необходимо обратить внимание на то, что если особенность планировки не допускает соблюдение данных параметров, допускается скорректировать высоту ступени до 20 см.
Необходимо обратить внимание на то, что если особенность планировки не допускает соблюдение данных параметров, допускается скорректировать высоту ступени до 20 см.
 Для того чтобы установить ограждение, требуется высверлить отверстия по краям ступеней.
Для того чтобы установить ограждение, требуется высверлить отверстия по краям ступеней.

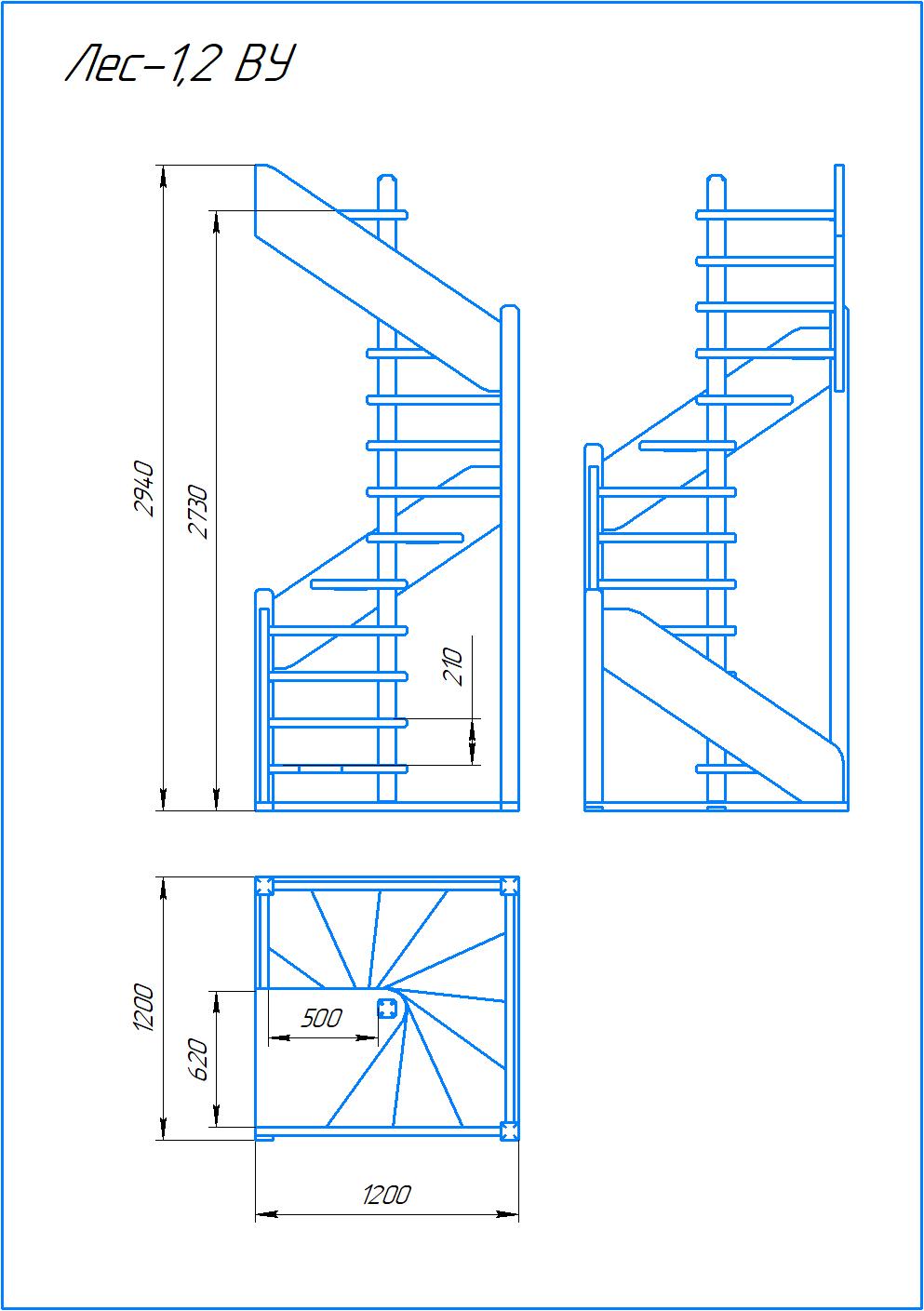
 Если соединить эти точки деления с соответствующими точками деления на линии подъема, то мы получим соответствующие передние грани ступеней (3 шаг).
Если соединить эти точки деления с соответствующими точками деления на линии подъема, то мы получим соответствующие передние грани ступеней (3 шаг).

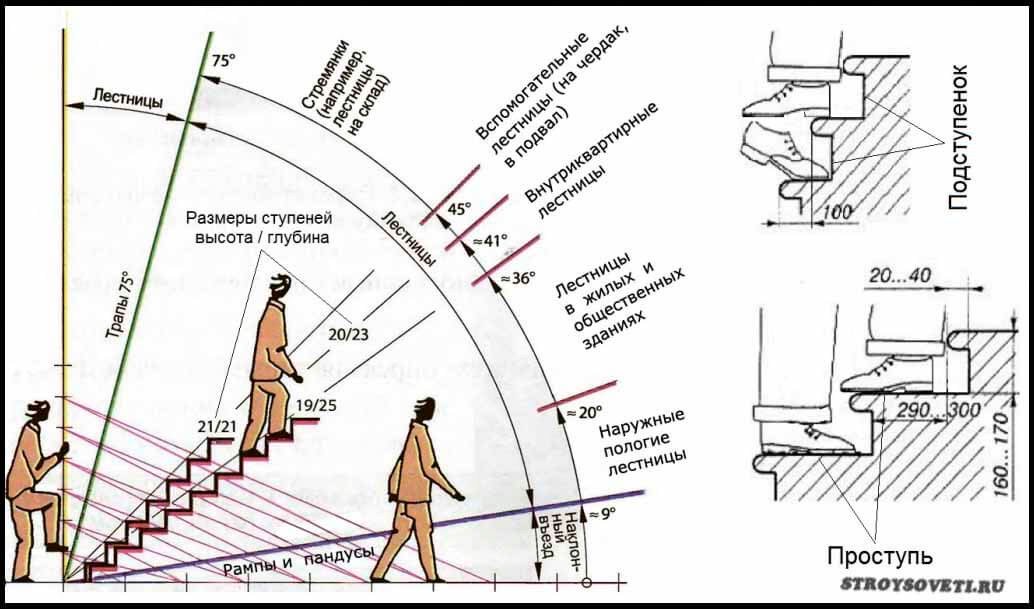


 Поле, зависящее от времени) должны иметь меньшие временные шаги
чем некоторая доля периода РЧ, чтобы частицы могли видеть
форму волны RF точно или вообще.(См. Пример SIMION: октуполь.)
Поле, зависящее от времени) должны иметь меньшие временные шаги
чем некоторая доля периода РЧ, чтобы частицы могли видеть
форму волны RF точно или вообще.(См. Пример SIMION: октуполь.) (См. Пример SIMION: Collision_hs1.)
(См. Пример SIMION: Collision_hs1.)