Теоретический вес арматуры таблица: Вес арматуры А3 » Металлобазы.ру
Удельный вес арматуры — для чего важен точный расчет, как расчитать, таблица
На чтение 5 мин. Просмотров 966 Обновлено
Наверноe. каждый хоть раз слышал об армировании конструкций, выполненных из железобетона. Процедура армирования достаточно кропотливая и, увы, не каждый ее еще выполнит качественно. Необходимо знать некоторые особенности и разбираться в таблице удельного веса.
Все это, безусловно, очень важно при армировании, да и при работе с железобетонными конструкциями. Сегодня мы поговорим про удельный вес арматуры. Для вашего удобства представлена таблица, которая позволит вам быстро ориентироваться.
Для чего необходим точный расчет массы армированных конструкций?
Для чего же нужен точный расчет и почему этому уделяется так много внимания? В первую очередь это необходимо в процессе строительных работ. Конечно, это итак понятно. Давайте углубимся в проблематику.
Все же, почему это так важно?
- Во-первых, при точном расчете массы армированных конструкций, мы сможем рассчитать и дать адекватную оценку стоимости всего процесса строительства, который, как вы знаете, обходится не в одну «копеечку».

- Во- вторых, при точном расчете массы армированных конструкций, мы сможем знать точную стоимость готового, уже построенного объекта. Это не менее важно, согласитесь.
Поэтому, в итоге можно сделать вывод, что это крайне важно для оценки объекта и строительства. Ведь, продавая тот или иной объект, нужно понимать какова себестоимость, а также при продажи объекта не остаться «в минусе».
Для того чтобы верно и правильно получать точные цифры расчета, нужно элементарно научиться считать массу той или иной армированной конструкции.
Как узнать массу погонного метра?
Для того чтобы узнать массу погонного метра, в первую очередь, необходимо на практике применить формулу. Именно при помощи формулы мы и узнаем массу погонного метра.
Конечно, многие специалисты советуют ориентироваться на уже готовые таблицы со значениями. Однако, для наиболее точного и подробного расчета, лучше всего воспользоваться формулой.
Представим, что у нас имеются такие показатели, как:
- M, которая будет обозначать теоретическую массу одного погонного метра;
- Π является постоянно действующей величиной, размер которой составляет = 3,14;
- d является наружным диаметром, исчисление которого осуществляется в такой единице измерения как мм;
- s обозначает толщину стенки и измеряется также в такой единице измерения, как мм;
- n данный показатель у нас будет представлен в виде: 1000/m ( смотрите обозначение).

- ρ обозначает плотность и измеряется в г/см3
Далее, что мы будет делать с этими показателями? Для расчета мы подставим их в формулу. Формула выглядит таким образом:
M (теоретическая масса одного погонного метра) равняется следующим показателям =Π (3,14) постоянный показатель умножает на d (наружный диаметр- толщина стенки). Затем это все умножается на толщину стенки вновь и на плотность. Далее, все то мы поделим на 1000.
Для вашего удобства, наглядно формула выглядит таким образом: m=Π*(d-s)*s*ρ/1000.
От чего зависит вес погонного метра?
От чего же зависит вес погонного метра? Вы наверно уже задавались этим вопросом, читая вышеприведенную информацию. Давайте и здесь разберемся.
В магазинах вы можете увидеть цену за 1 тонну погонного метра. Нам такой показатель не подходит. Поэтому, мы будем переводить погонные метры в тонну.
Количество погонных метров в одной тонне будет, прежде всего, зависеть от такого, каков диаметр имеющихся у арматуры прутьев. Запомните! Чем больше диаметр прутьев, тем меньше будет в 1 тонне метров.
Запомните! Чем больше диаметр прутьев, тем меньше будет в 1 тонне метров.
Таблица
Для вашего удобства можно использовать таблицу с уже имеющимися значениями.
| Диаметр арматуры (мм) | Вес кг/метр | Метров в 1 тонне |
| 5.5 | 0.187 | 5347 |
| 6 | 0.222 | 4504 |
| 8 | 0.395 | 2531 |
| 10 | 0.617 | 1620 |
| 12 | 0.888 | 1126 |
| 14 | 1.210 | 826 |
| 16 | 1.580 | 633 |
| 18 | 2.000 | 500 |
| 20 | 2.470 | 405 |
| 22 | 2.980 | 335 |
| 25 | 3.850 | 260 |
| 28 | 4.830 | 207 |
| 32 | 6.310 | 158 |
| 36 | 7.990 | 125 |
| 40 | 9.870 | 101 |
| 45 | 12.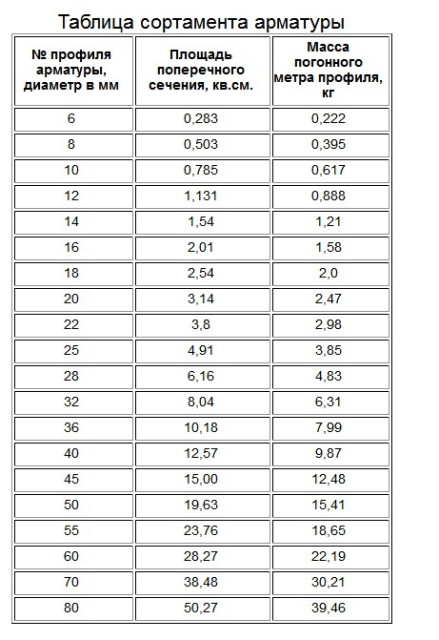 480 480 | 80 |
| 50 | 15.410 | 65 |
Расчет веса арматуры
Существует всего несколько способов, при помощи которых можно рассчитать вес арматуры. Давайте разберем каждый по отдельности:
- Первый способ включает в себя необходимостью воспользоваться помощью онлайн-калькулятором металлопроката. Для того чтобы произвести верный расчет, достаточно того, что вы будете знать диаметр у металлического прута и длину непосредственно самого прута, который будет выражен в погонных метрах. В специально предназначенной программе, нужно вписать соответствующие данные и произвести затем расчет.
- Второй способ предполагает воспользоваться таблицей. Таким способ расчета подойдет тогда, когда нет возможности воспользоваться помощью онлайн-калькулятора. Однако! Вам должна быт известна маркировка самой арматуры даже для работы с калькулятором. Для нахождения массы, воспользуйтесь первым и вторым столбиком таблицы.
 Обратите особое внимание на то, что в самом первом столбике необходимо найти тот диаметр, который интересует прежде вас! В той же строке, но уже в третьем столбике вы увидите массу, которая будет выражена в погонных метрах.
Обратите особое внимание на то, что в самом первом столбике необходимо найти тот диаметр, который интересует прежде вас! В той же строке, но уже в третьем столбике вы увидите массу, которая будет выражена в погонных метрах. - Третий способ предусматривает расчет при помощи формулы. Если у вас нет возможности найти таблицу или же воспользоваться калькулятором, то можно произвести расчет при помощи формулы. Несмотря на то, что процесс расчета кропотливый и не такой уж и простой, вы получите точно верные результаты.
Востребование арматуры различного диаметра в строительстве
Арматура, безусловно, бывает разнообразная и в том числе, разного диаметра. Строительство — это очень широкое понятие. Ведь строить можно что угодно для разной стройки подойдет разный диаметр арматуры.
Арматура помогает в строительстве тем, что способна создавать каркас и при помощи нее монтаж получается простым и легким. Поэтому, каждая строительная компания и любой строитель пользуется различными диаметрами арматуры. Все, безусловно, зависит от масштабности стройки.
Все, безусловно, зависит от масштабности стройки.
Безусловно, каждый в ходе стройки старается максимально верно производить расчеты. Поэтому, чтобы ваша стройка принесла вам максимум прибыли и вы действительно умели ориентироваться в таких важных деталях, пользуйтесь всеми возможными источниками.
Теоретический и фактический вес арматуры Главная
Теоретический вес арматуры — это то значение веса, которое мы получаем в результате расчётов, без непосредственного взвешивания арматуры на весах. Для расчёта теоретического веса арматуры нам нужно опираться не на физические данные, на удельный вес арматурной стали, а лучше «заглянуть» в ГОСТ и взять там ВЕС ПОГОННОГО МЕТРА АРМАТУРЫ — это будет удобнее и как ни странно, точнее. Не забывайте, что теоретический вес арматуры указанный в ГОСТЕ приводится для условного, эталонного метра арматуры определённого диаметра. А вот на сколько реальная, «живая» арматура будет близка к эталону — это вопрос к производителю арматурной стали. надо сказать, что в целом, заводы изготавливающие арматуру, находятся в положении «буриданова осла» и разрываются между двумя тенденциями. С одной стороны, очень уж выгодно производителю арматуры, хоть на «копеечку» занизить вес метра арматурной стали. При больших объёмах производства арматуры экономия получается просто фантастическая. С другой стороны «сильно увлекаться» этим нельзя. Существуют кроме всего прочего ещё и контролирующие службы, да и вообще, ведь все инженерные расчёты конструкций с арматурой базируются на более или менее точном соответствии сортамента эталонным значениям. То есть, настоящая «живая» арматура обычно довольно точно «попадает» в табличные данные ГОСТа на арматуру.
надо сказать, что в целом, заводы изготавливающие арматуру, находятся в положении «буриданова осла» и разрываются между двумя тенденциями. С одной стороны, очень уж выгодно производителю арматуры, хоть на «копеечку» занизить вес метра арматурной стали. При больших объёмах производства арматуры экономия получается просто фантастическая. С другой стороны «сильно увлекаться» этим нельзя. Существуют кроме всего прочего ещё и контролирующие службы, да и вообще, ведь все инженерные расчёты конструкций с арматурой базируются на более или менее точном соответствии сортамента эталонным значениям. То есть, настоящая «живая» арматура обычно довольно точно «попадает» в табличные данные ГОСТа на арматуру.
Фактический вес арматуры — это то значение веса, которое мы получаем при непосредственном взвешивании на специальных весах, имеющих свою погрешность. Поэтому доверять взвешиванию можно, но осторожно. Торговля арматурой знает множество примеров сознательного и случайного обвеса покупателей и тут влияние контролирующих органов сказывается слабо.
Итак, вы хотите теперь узнать, как сделать расчёт веса арматуры имея перед глазами таблицу? Кстати, вы можете скачать таблицу бесплатно, мы будем только рады, если она вам пригодится для того, чтобы узнать, как определить вес арматуры. На самом деле пользоваться таблицей расчёта веса арматуры очень просто и удобно, хоть она и выглядит несколько «пугающе», на первый взгляд (мало букафф и многа цифер). Есть довольно
 Вам же он осуществляет продажу арматуры 12 мм в метраже, в погонных метрах, которых вам нужно ровно 25 м. То есть цена арматуры 12 мм за тонну, совершенно вам ничего не говорит. Чтобы как-то перевести имеющееся у вас количество погонных метров арматуры 12 мм в «категории близкие к: цена тонны арматуры 12мм», вам нужно сделать расчёт сколько же весят ваши 25 метров арматуры диаметром 12 мм. Находим в таблице расчёта веса арматуры строчку — вес погонного метра арматуры 12 мм (мы уже сделали это за вас — смотри выше), на против указано значение веса метра арматуры 12 мм в килограммах — 0, 89 кг. Теперь, зная вес одного метра арматуры 12 мм, мы должны умножить его на количество метров — 0, 89 х 25 = 22, 25 кг. То есть, ваши 25 погонных метров, весят ровно 22, 25 кг. Это расчёт веса арматуры в результате которого вы получаете
Вам же он осуществляет продажу арматуры 12 мм в метраже, в погонных метрах, которых вам нужно ровно 25 м. То есть цена арматуры 12 мм за тонну, совершенно вам ничего не говорит. Чтобы как-то перевести имеющееся у вас количество погонных метров арматуры 12 мм в «категории близкие к: цена тонны арматуры 12мм», вам нужно сделать расчёт сколько же весят ваши 25 метров арматуры диаметром 12 мм. Находим в таблице расчёта веса арматуры строчку — вес погонного метра арматуры 12 мм (мы уже сделали это за вас — смотри выше), на против указано значение веса метра арматуры 12 мм в килограммах — 0, 89 кг. Теперь, зная вес одного метра арматуры 12 мм, мы должны умножить его на количество метров — 0, 89 х 25 = 22, 25 кг. То есть, ваши 25 погонных метров, весят ровно 22, 25 кг. Это расчёт веса арматуры в результате которого вы получаете Сразу скажу — взвешивать арматуру ЖЕЛАТЕЛЬНО, но не менее желательно при возможности и пересчитывать теоретический вес, для проверки. На самом деле теоретический вес арматуры из таблицы — это довольно точный ориентир. Это лучший способ, как определить вес арматуры, им пользуются все практики строители и производители металлоконструкций. ВНИМАНИЕ!!! Взвешивание арматуры на весах покажет немного другой вес, отличный от указанного теоретического значения в таблице весов арматуры — это нормально, всё в пределах допуска, обусловленного спецификой технологии изготовления арматуры на заводе изготовителе металлопроката. Но
На самом деле теоретический вес арматуры из таблицы — это довольно точный ориентир. Это лучший способ, как определить вес арматуры, им пользуются все практики строители и производители металлоконструкций. ВНИМАНИЕ!!! Взвешивание арматуры на весах покажет немного другой вес, отличный от указанного теоретического значения в таблице весов арматуры — это нормально, всё в пределах допуска, обусловленного спецификой технологии изготовления арматуры на заводе изготовителе металлопроката. Но

Сортамент арматуры таблица — Бетонные и железобетонные работы
Главная » Бетонные и железобетонные работыАвтор Admin На чтение 2 мин. Просмотров 119 Опубликовано
| Номинальный диаметр, мм | Площадь поперечного сечения, см2 | Масса1 м | |
| теоретическая, кг | допускаемое отклонение, проц. | ||
| 6 | 0,283 | 0,222 | +10 |
| 7 | 0,385 | 0,302 | ?9 |
| 8 | 0,503 | 0,395 | |
| 10 | 0,785 | 0,617 | +5,5 |
| 12 | 1,131 | 0,888 | ?7 |
| 14 | 1,54 | 1,21 | +4 |
| 16 | 2,01 | 1,58 | ?6 |
| 18 | 2,64 | 2 | +3,5 |
| 20 | 3,14 | 2,47 | ?5,5 |
| 22 | 3,80 | 2,98 | +3 |
| 25 | 4,91 | 3,85 | |
| 28 | 6,16 | 4,83 | +3 |
| 32 | 8,04 | 6,31 | ?5 |
| 36 | 10,18 | 7,99 | |
| 40 | 12,58 | 9,87 | |
| 45 | 15,90 | 12,48 | |
| 50 | 19,63 | 15,41 | +2 |
| 55 | 23,76 | 18,65 | ?4 |
| 60 | 28,27 | 22,19 | |
| 70 | 38,48 | 30,21 | |
| 80 | 50,27 | 39,46 | |
Арматурная проволока
| Номинальный диаметр, мм | Расчетная площадь поперечного сечения,мм2 | Теоретическая масса I м, кг, классов | Номинальный диаметр, мм | Расчетная площадь поперечного сечения, мм2 | Теоретическая масса I м, кг, классов В ? II, Bp-II | |
| В-I, B-II, Bp-II | Bp-I | |||||
| 3 | 7,06 | 0,056 | 0,052 | 6 | 28,3 | 0,222 |
| 4 | 12,56 | 0,099 | 0,092 | 7 | 38,5 | 0,302 |
| 5 | 19,63 | 0,154 | 0,144 | 8 | 50,3 | 0,395 |
Арматурные канаты
| Класс | Диаметр, мм | Расчетная площадь поперечного сечения, см2 | Расчетная масса1 м, кг при шаге свивки | |||
| условный | Номинальный, Д | |||||
| 10Д | 16Д | |||||
| К-7 | 4,5 | 4,65 | 0,127 | 0,102 | 0,100 | |
| 6 | 6,20 | 0,227 | 0,181 | 0,173 | ||
| 7,5 | 7,75 | 0,354 | 0,283 | 0,279 | ||
| 9 | 9,30 | 0,510 | 0,407 | 0,402 | ||
| 12 | 12,40 | 0,906 | 0,724 | 0,714 | ||
| 15 | 12,50 | 1,416 | 1,132 | 1,116 | ||
| Класс | Номинальный диаметр, мм | Расчетная площадь поперечного сечения, см2 | Теоретическая масса1 м, кг |
| К-19 | 14 | 1,287 | 1,020 |
| К-2*7 | 18 | 1,019 | 1,801 |
| К-2*7 | 25 | 1,812 | 1,428 |
| К3*7 | 10 | 0,381 | 0,299 |
| К3*7 | 13 | 0,678 | 0,583 |
| КЗ*7 | 16,5 | 1,062 | 0,825 |
| К3*7 | 20 | 1,527 | 1,209 |
| КЗ* 19 | 16,5 | 1,031 | 0,795 |
| КЗ* 19 | 22 | 1,809 | 1,419 |
| Вид арматуры и документы, регламентирующие качество | Класс | Диаметры арматуры, в мм | |||||||||||||||||||||
3 | 4 | 4,5 | 5 | 6 | 7 | 7,5 | 8 | 9 | 10 | 12 | 14 | 15 | 16 | 18 | 20 | 22 | 25 | 28 | 32 | 36 | 40 | ||
| Стержневая горячекатаная гладкая, ГОСТ 5781-75 | A-I | + | + | + | + | + | + | + | + | ||||||||||||||
| Стержневая горячекатаная периодического профиля,ГОСТ 5781-75 | A-II | + | + | + | + | + | + | + | + | + | + | — | — | ||||||||||
| A-III, Ат-Ш | + | — | + | + | + | + | + | + | + | + | + | + | + | + | + | ||||||||
| A-IIIb | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | ||||||||
ГОСТ 5. 1459-72 * 1459-72 * | A-IV, ?т-IVc | + | + | + | + | + | |||||||||||||||||
| Стержневая термически упрочненная периодического профиля ГОСТ 10884-81 | A-IV | — | — | — | — | — | — | — | — | — | — | ||||||||||||
| A-V, ?т-V | + | + | + | + | + | + | |||||||||||||||||
| A-V, ?т-VI | + | + | + | + | + | ||||||||||||||||||
| Обыкновенная арматурная проволока гладкая, ГОСТ 6727-80 | B-I | — | — | — | |||||||||||||||||||
| То же, периодического профиля ГОСТ 6727-80 | Bp-I | + | + | + | |||||||||||||||||||
| Высокопрочная арматурная проволока гладкая,ГОСТ 7348-81 | B-II | — | + | + | + | ||||||||||||||||||
| То же, периодического профиля ГОСТ 7348-81 | Bp-II | ||||||||||||||||||||||
| Арматурные канаты ГОСТ13840-68 * | К-7 | + | + | + | + | ||||||||||||||||||
| Арматурные канаты ГОСТ 13840-68* | К-19 | ||||||||||||||||||||||
Условные обозначения: + рекомендуемые к использованию диаметры и классы арматурной эффективной стали, — — исключенные из сортамента диаметры и классы арматурной стали; 0 — сортамент.
Примечания: 1. Диаметры арматуры приняты согласно сортаменту по соответствующим ГОСТ или ТУ с учетом указаний по области применения различных классов стали; исключенные из сортамента диаметры и классы арматурной стали; 0 — сортамент сталей -по пп. 2.18—2—25 СНиП П-21-75. 2. Сталь класса A-IIIb диаметрами более20 мм, арматурных упрочняемая вытяжкой на предприятиях стройиндустрии, допускается к применению в качестве напрягаемой арматуры при отсутствии арматурной стали более высоких классов. 3. При изготовлении конструкций допускается замена проволоки класса Bp-I на имеющуюся в наличии проволоку класса В-1.
Сталь, применяемая для арматуры, не должна иметь на поверхности загрязнений и ржавчины.
Теоретический вес 1 погонного метра стальной рифленой арматура А3
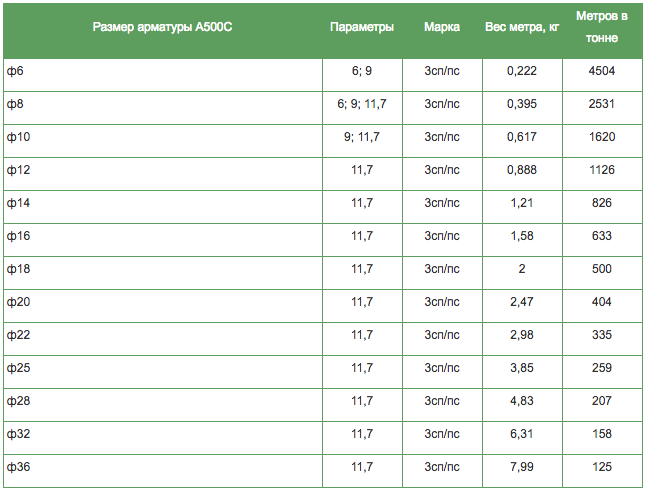
Теоретический вес 1 метра погонного стальной рифленой арматура А3 (А500С / S500)
| Диаметр арматуры, мм | Вес 1 метра погонного арматуры, кг | Количество метров арматуры в 1 тонне | Площадь поперечного сечения арматуры, см2 |
| 6 | 0,222 | 4504,5 | 0,283 |
| 8 | 0,395 | 2531,65 | 0,503 |
| 10 | 0,617 | 1620,75 | 0,785 |
| 12 | 0,888 | 1126,13 | 1,131 |
| 14 | 1,21 | 826,45 | 1,54 |
| 16 | 1,58 | 632,91 | 2,01 |
| 18 | 2 | 500 | 2,54 |
| 20 | 2,47 | 404,86 | 3,14 |
| 22 | 2,98 | 335,57 | 3,8 |
| 25 | 3,85 | 259,74 | 4,91 |
| 28 | 4,83 | 207,04 | 6,16 |
| 32 | 6,31 | 158,48 | 8,04 |
| 36 | 7,99 | 125,16 | 10,18 |
| 40 | 9,87 | 101,32 | 12,57 |
| 45 | 12,48 | 80,13 | 15 |
| 50 | 15,41 | 64,89 | 19,63 |
| 55 | 18,65 | 53,62 | 23,76 |
| 60 | 22,19 | 45,07 | 28,27 |
| 70 | 30,21 | 33,1 | 38,48 |
| 80 | 39,46 | 25,34 | 50,27 |
Таблица в соответствии с требованиями ГОСТ 5781-82
Арматура погонаж в 1 тонне и вес погонного метра
Зачастую при проведении строительных работ требуется перевести вес арматуры в погонные метры и наоборот ― специально для этого мы сделали удобную таблицу.
Длина (погонаж) и вес арматуры ― важные параметры при приобретении металлопроката, поскольку знание этих величин делает Ваше строительство более удобным и предсказуемым.
О том, для чего нужно армирование при строительстве, читайте в статьях:
Зачем нужно армирование кладки из кирпича;
Армопояс — устройство и назначение при строительстве из газобетона.
Таблица теоретического веса строительной арматуры А3
Арматура ГОСТ марка стали А500С | Вес метра погонного, кг | Количество метров в тонне, м |
Арматура А3 Ø 6 мм | 0,222 | 4504,5 |
Арматура А3 Ø 8 мм | 0,395 | 2531,65 |
Арматура А3 Ø 10 мм | 0,617 | 1620,75 |
Арматура А3 Ø 12 мм | 0,888 | 1126,13 |
Арматура А3 Ø 14 мм | 1,21 | 826,45 |
Арматура А3 Ø 16 мм | 1,58 | 632,91 |
Арматура А3 Ø 18 мм | 2 | 500 |
Арматура А3 Ø 20 мм | 2,47 | 404,86 |
Арматура А3 Ø 22 мм | 2,98 | 335,57 |
Арматура А3 Ø 25 мм | 3,85 | 259,74 |
Арматура А3 Ø 28 мм | 4,83 | 207,04 |
Арматура А3 Ø 32 мм | 6,31 | 158,48 |
Арматура А3 Ø 36 мм | 7,99 | 125,16 |
Арматура А3 Ø 40 мм | 9,87 | 101,32 |
Как использовать Z-таблицу
- Образование
- Математика
- Статистика
- Как пользоваться Z-таблицей
Для чайников-потребителей
Вы можете использовать таблицу Z-оценок, чтобы найти полный набор вероятностей «меньше» для широкого диапазона z-значений с использованием формулы z-score. Ниже вы найдете таблицу положительных и отрицательных z-оценок. При выяснении статистических проблем убедитесь, что вы понимаете, как использовать таблицу Z- для нахождения желаемых вероятностей.Используйте эти таблицы, чтобы понять таблицу z-значений.
Ниже вы найдете таблицу положительных и отрицательных z-оценок. При выяснении статистических проблем убедитесь, что вы понимаете, как использовать таблицу Z- для нахождения желаемых вероятностей.Используйте эти таблицы, чтобы понять таблицу z-значений.
Таблица Z Score Примеры задач
Используйте эти примеры математических задач для z-показателя, чтобы выучить формулу z-показателя
Что такое
Ответ: 0,9332
Чтобы найти ответ с помощью таблицы Z- , найдите, где строка для 1,5 пересекается со столбцом для 0,00; это значение составляет 0,9332. Таблица Z- показывает только вероятности «меньше чем», поэтому она дает вам именно то, что вам нужно для ответа на этот вопрос. Примечание: Нет вероятности точно в одной точке, поэтому
Что такое
Ответ: 0,0668
Используйте таблицу Z-, чтобы найти, где строка для 1,5 пересекается со столбцом для 0,00, то есть 0,9332.
 Поскольку таблица Z- дает вам только вероятности «меньше», вычтите P ( Z <1,5) из 1 (помните, что полная вероятность для нормального распределения равна 1.00, или 100%):
Поскольку таблица Z- дает вам только вероятности «меньше», вычтите P ( Z <1,5) из 1 (помните, что полная вероятность для нормального распределения равна 1.00, или 100%):Что такое
Ответ: 0,5328
Чтобы найти вероятность того, что Z находится между двумя значениями, используйте таблицу Z-, чтобы найти вероятности, соответствующие каждому значению z-, а затем найдите разницу между вероятностями.
Здесь вам нужна вероятность того, что Z находится в диапазоне от –0,5 до 1,0. Во-первых, используйте таблицу Z- , чтобы найти значение, в котором находится строка для –0.5 пересекается со столбцом 0,00, равным 0,3085. Затем найдите значение, в котором строка 1,0 пересекается со столбцом 0,00, то есть 0,8413.
Поскольку таблица Z- дает вам только вероятности «меньше чем», найдите разницу между вероятностью меньше 1,0 и вероятностью меньше –0,5:
Что такое
Ответ: 0,6826
Чтобы найти вероятность того, что Z находится между двумя значениями, используйте таблицу Z-, чтобы найти вероятности, соответствующие каждому значению z-, а затем найдите разницу между вероятностями.

Здесь вам нужна вероятность того, что Z находится между –1,0 и 1,0. Во-первых, используйте таблицу Z-, чтобы найти значение, в котором строка для –1,0 пересекается с 0,00, что составляет 0,1587. Затем найдите значение, в котором строка 1,0 пересекается со столбцом 0,00, то есть 0,8413.
Поскольку таблица Z- дает вам только вероятности «меньше», найдите разницу между вероятностью меньше 1,0 и вероятностью меньше –1,0:
Если вам нужно больше практики по этой и другим темам из вашего курса статистики, посетите 1001 статистические практические задачи для чайников, чтобы приобрести онлайн-доступ к 1001 статистическим практическим задачам! Мы можем помочь вам отслеживать вашу успеваемость, определять, где вам нужно учиться, и создавать индивидуальные наборы задач, чтобы улучшить свои статистические навыки.
Алгоритмы обучения с подкреплением
Доступ
Почему я написал эту книгу? Хороший вопрос! Существует множество действительно замечательных книг по обучению с подкреплением.Так почему новая книга? У меня были эгоистичные причины: мне нужна была небольшая книга, которая, тем не менее, содержала основные идеи, лежащие в основе современных алгоритмов RL (еще в 2010 году), обсуждение их относительных сильных и слабых сторон с намеками на то, что известно (и не известно, но было бы хорошо узнать) об этих алгоритмах. Аннотация Обучение с подкреплением — это парадигма обучения, связанная с обучением управлению системой, чтобы максимизировать числовой показатель эффективности, который выражает долгосрочную цель.Что отличает обучение с подкреплением от обучения с учителем, так это то, что учащемуся предоставляется только частичная обратная связь о его предсказаниях. Кроме того, прогнозы могут иметь долгосрочные эффекты, влияя на будущее состояние управляемой системы. Таким образом, время играет особую роль. Целью обучения с подкреплением является разработка эффективных алгоритмов обучения, а также понимание достоинств и ограничений алгоритмов. Обучение с подкреплением представляет большой интерес из-за большого количества практических приложений, для решения которых оно может использоваться, начиная от задач в области искусственного интеллекта и заканчивая исследованиями операций или разработкой управления. Содержание
АлгоритмыКнига, как следует из названия, описывает ряд алгоритмов. Это следующие. Для алгоритмов, имена которых выделены жирным шрифтом, также дается псевдокод.
Другие уникальные особенности книгиВ книге рассматриваются следующие методы приближения функций:
Кроме того, в нем обсуждаются относительные достоинства «пакетных» (LS-тип) и инкрементных (TD-типов) алгоритмов.
влияние выбора метода аппроксимации функции (можем ли мы переобучить в обучении с подкреплением?),
различные теоретически обоснованные алгоритмы онлайн-обучения (когда-нибудь задумывались о том, что должен делать эффективный метод исследования?),
актерско-критические алгоритмы,
и больше. Новые результаты в книге
Учебник, слайды Некоторым людям намного легче учиться на слайдах.
Исправлений (последнее обновление: 25 июня 2018 г.) В идеальном мире мы бы публиковали без ошибок.Мир не идеален. Второй лучший способ — это вести список ошибок (и обновлять pdf!).
Для вашего удобства здесь я даю вам список ошибок как в формате pdf, так и в формате html. Вышеупомянутые опечатки основаны в основном на списке, предоставленном Габором, который заслуживает большой благодарности за то, что так внимательно прочитал текст. Я также в долгу перед
Сотэцу Коямада
которые совсем недавно дали мне еще один длинный список опечаток.
Ранее (и совсем недавно) несколько человек читали разные части проекта и вносили полезные предложения, которые я попробовал.
Спасибо! Все остальные ошибки — мои. |
Нормы арматуры
Ссылки по теме
Стандарты, относящиеся к армированию и предварительному напряжению бетона:
EN 10138 — Предварительно напряженная сталь
Стали предварительного напряжения в четырех частях:
- EN 10138-1. Стали предварительного напряжения. Общие требования
- EN 10138-2.Стали предварительного напряжения. Провод
- EN 10138-3. Стали предварительного напряжения.
 Strand
Strand - EN 10138-4. Стали предварительного напряжения. Бары
Эти детали в настоящее время находятся в разработке.
EN 10080: Сталь для армирования бетона, свариваемая, ребристая арматурная сталь
BS EN 10080: 2005
Свариваемая сталь для армирования бетона стала предметом европейского стандарта BS EN 10080.Этот стандарт много лет ходил туда-сюда в поисках прагматичного соглашения между европейцами о том, как стандартизировать арматуру. Другими словами, потребовалось много времени, чтобы перейти от обязательного стандарта (который Европейская комиссия попросила CEN подготовить) к гармонизированному стандарту. В 2008 году его пришлось отменить как гармонизированный стандарт, поскольку не были соблюдены законодательные требования некоторых стран в отношении дополнительных свойств арматуры. Однако он был внедрен в Великобритании в конце 2005 года, и его последующая отмена не повлияла на BS 4449 и т. Д.
BS EN 10080: 2005 не дает фактических спецификаций или цифр; это оставлено на усмотрение национальных стандартов.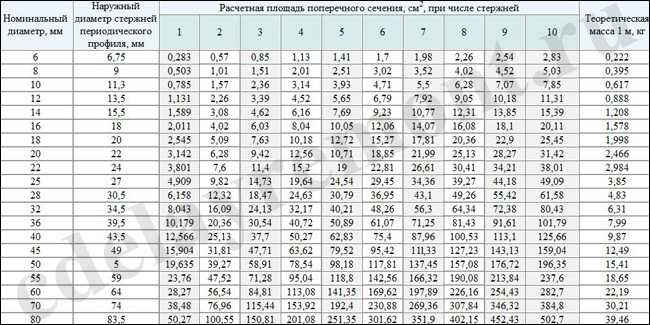
Требует, чтобы технические классы определялись значениями:
- R e , предел текучести;
- R m / R e , отношение прочности на разрыв / предел текучести,
- A gt , Общее удлинение в процентах при максимальном усилии,
- R e, act / R e, nom (где применимо), отношение фактического значения предела текучести к заданному,
- усталостной прочности,
- производительность изгиба,
- свариваемость,
- прочность сцепления,
- допусков и
- габаритов.
Он содержит информативное приложение ZA, в котором описывается, как стандарт может быть использован для целей маркировки CE. Обратите внимание, что знак CE — это , а не как знак качества. Он просто идентифицирует продукт как соответствующий основному требованию, установленному Европейской Комиссией в ее «полномочиях» перед CEN. Маркировка CE не является требованием стандарта BS 4449: 2005, и усиление не может иметь маркировку CE, поскольку гармонизированный стандарт был отменен.
Маркировка CE не является требованием стандарта BS 4449: 2005, и усиление не может иметь маркировку CE, поскольку гармонизированный стандарт был отменен.
BS EN ISO 17660: Сварка арматурной стали
Этот стандарт состоит из двух частей:
- BS EN ISO 17660-1: 2006.Сварка. Сварка арматурной стали — Соединения сварные несущие
- BS EN ISO 17660-2: 2006. Сварка. Сварка арматурной стали — Ненесущие сварные соединения
BS 4449: 2005 Сталь для армирования бетона Свариваемая арматурная сталь, стержень, рулон и размотанный продукт
Это была полная редакция стандарта, определяющая три класса арматуры, соответствующие ныне отмененному стандарту BS EN 10080: B500A, B500B и B500C. Характерный предел текучести установлен на уровне 500 МПа, а свойства при растяжении и пластичность трех марок описаны в таблице 1.
Характерные свойства при растяжении
Марка | Предел текучести R e МПа | Отношение предел прочности / предела текучести R м / R e | Полное удлинение при максимальном усилии, A gt % |
|---|---|---|---|
B500A | 500 | 1. | 2,5 б |
B500B | 500 | 1,08 | 5,0 |
B500C | 500 | 1.15, <1,35 | 7,5 |
a R м / R c Характеристика составляет 1,02 для размеров менее 8 мм b A gt характеристика составляет 1,0% для размеров менее 8 мм Указанные значения R c характерны для p = 0,95 Указанные значения R m / R c и A gt характерны для p = 0.90 Рассчитайте значения R м и R c , используя номинальную площадь поперечного сечения | |||
Абсолютно допустимое значение предела текучести 650 МПа. Оставить комментарий | |||



 Обратите особое внимание на то, что в самом первом столбике необходимо найти тот диаметр, который интересует прежде вас! В той же строке, но уже в третьем столбике вы увидите массу, которая будет выражена в погонных метрах.
Обратите особое внимание на то, что в самом первом столбике необходимо найти тот диаметр, который интересует прежде вас! В той же строке, но уже в третьем столбике вы увидите массу, которая будет выражена в погонных метрах.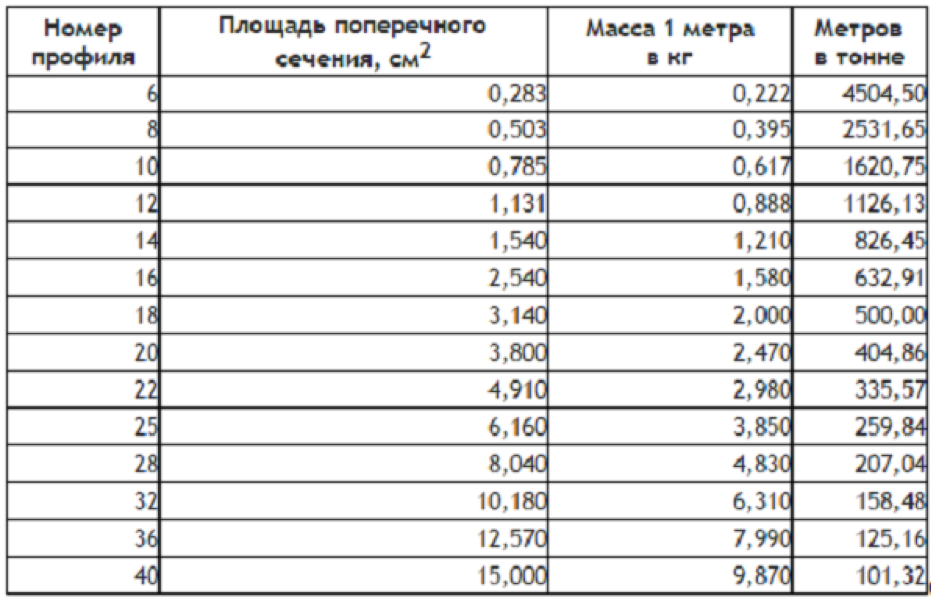 Поскольку таблица Z- дает вам только вероятности «меньше», вычтите P ( Z <1,5) из 1 (помните, что полная вероятность для нормального распределения равна 1.00, или 100%):
Поскольку таблица Z- дает вам только вероятности «меньше», вычтите P ( Z <1,5) из 1 (помните, что полная вероятность для нормального распределения равна 1.00, или 100%):
 Последнее обновление:
12 марта 2019 г.,
Последнее обновление:
12 марта 2019 г., Если получится, время покажет. Или вы можете, отправив мне электронное письмо на csaba.szepesvari@gmail.com
Если получится, время покажет. Или вы можете, отправив мне электронное письмо на csaba.szepesvari@gmail.com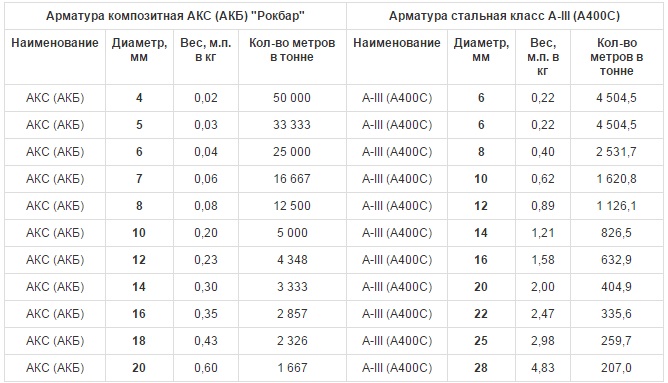 В этой книге мы сосредоточимся на тех алгоритмах обучения с подкреплением, которые основаны на мощной теории динамического программирования. Мы даем достаточно полный каталог задач обучения, описываем основные идеи, отмечаем большое количество современных алгоритмов, после чего обсуждаем их теоретические свойства и ограничения.
В этой книге мы сосредоточимся на тех алгоритмах обучения с подкреплением, которые основаны на мощной теории динамического программирования. Мы даем достаточно полный каталог задач обучения, описываем основные идеи, отмечаем большое количество современных алгоритмов, после чего обсуждаем их теоретические свойства и ограничения. 1 Сжатия и теорема Банаха о неподвижной точке 65
1 Сжатия и теорема Банаха о неподвижной точке 65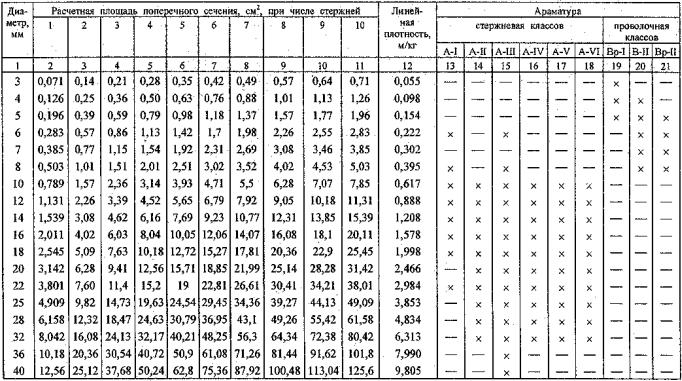 28
28 57
57 Упоминаются некоторые связи с другими частями литературы (помимо машинного обучения).Это включает в себя подключение LSTD (и связанных методов) к Z-оценке (из статистики), методы аппроксимации выборочного среднего (из исследования операций) или подключение алгоритмов градиента политики к методам отношения правдоподобия (из оптимизации моделирования). Вообще в книге много указателей на литературу. Я думаю, что книги дают
Упоминаются некоторые связи с другими частями литературы (помимо машинного обучения).Это включает в себя подключение LSTD (и связанных методов) к Z-оценке (из статистики), методы аппроксимации выборочного среднего (из исследования операций) или подключение алгоритмов градиента политики к методам отношения правдоподобия (из оптимизации моделирования). Вообще в книге много указателей на литературу. Я думаю, что книги дают  Мы с Ричем провели в июле на AAAI-2010 учебник, основанный на этой книге.
Веб-страница руководства находится здесь.
Мы использовали следующие слайды:
Мы с Ричем провели в июле на AAAI-2010 учебник, основанный на этой книге.
Веб-страница руководства находится здесь.
Мы использовали следующие слайды: включить.Они включают:
включить.Они включают: Strand
Strand 05 a
05 a 